AcWing《寒假每日一题（提高组）》笔记

持续更新中…

Week1

AcWing 1402. 星空之夜

思路：

用dfs从左到右逐行找到所有连通块，每找到一个连通块就立即用字母编号，这样可保证矩阵是字典顺序最小的。

为了比较不同星群，采用哈希值比较，由于星群的变换只有翻转和旋转（90°，180°，270°），故可用连通块内两两之间的欧几里得距离作为哈希值。

代码实现：

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 105;
const double eps = 1e-6;
char g[N][N];
int n, m;

typedef pair<int, int> PII;
PII q[510];     // 星群个数不超过500个
int top;        // 队尾指针

// 计算欧氏距离
double get_distance(PII a, PII b) {
    double temp_1 = (a.first - b.first) * (a.first - b.first);
    double temp_2 = (a.second - b.second) * (a.second - b.second);
    return sqrt(temp_1 + temp_2);
}

// 计算连通块的哈希值
double get_hash() {
    double res = 0.0;
    for (int i = 0; i < top; i++)
        for (int j = i + 1; j < top; j++) 
            res += get_distance(q[i], q[j]);
    return res;
}

// 判断当前连通块需要填充的字符
char get_char(double hash_code) {
    static double blocks[30];   // 最多27个不同的星群
    static int id = 0;
    for (int i = 0; i < id; i++)
        if (fabs(hash_code - blocks[i]) < eps)
            return (char) ('a' + i);        // 找到相似的星群
    blocks[id++] = hash_code;               // 保存新的星群
    return (char) ('a' + id - 1);
}

// 为连通块填充字符
void paint(char c) {
    for (int i = 0; i < top; i++) {
        int x = q[i].first;
        int y = q[i].second;
        g[x][y] = c;
    }
}

void dfs(int x, int y) {
    q[top++] = {x, y};      // 保存方格坐标
    g[x][y] = '0';      // 标记已走过
    for (int i = x - 1; i <= x + 1; i++) {
        for (int j = y - 1; j <= y + 1; j++) {
            if (i == x && j == y) continue;     // 自身
            if (i >= 0 && i < n && j >= 0 && j < m && g[i][j] == '1')
                dfs(i, j);          
        }
    }
}

int main() {
    cin >> m >> n;
    for (int i = 0; i < n; i++) cin >> g[i];

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            if (g[i][j] == '1') {
                top = 0;        // 清空上一个连通块的信息，记录下一个连通块
                dfs(i, j);      // 找到当前连通块占据的所有方格坐标

                double hash_code = get_hash();      // 计算当前连通块的哈希值
                char c = get_char(hash_code);                // 返回当前连通块的字符编号

                paint(c);           // 为当前连通块填充字符
            }

    for (int i = 0; i < n; i++) puts(g[i]);

    return 0;
}

AcWing 479. 加分二叉树

思路：

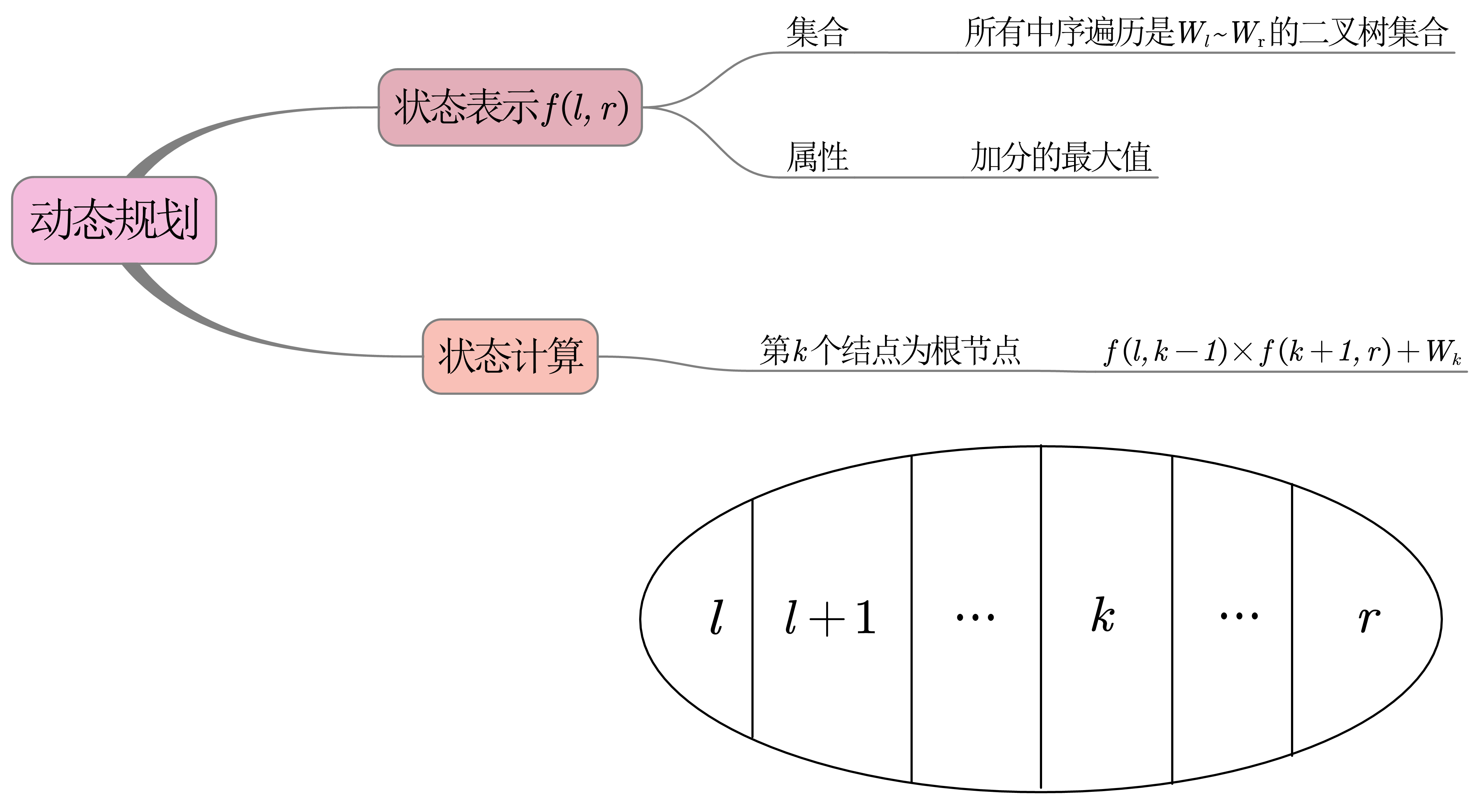
中序遍历序列可用区间DP处理

用三重循环遍历所有情况：区间长度→左端点→根节点

代码实现：

#include <iostream>
using namespace std;
const int N = 33;

int n, w[N], f[N][N], root[N][N];

void dfs(int l, int r) {
    if (l > r) return;
    printf("%d ", root[l][r]);
    dfs(l, root[l][r] - 1);
    dfs(root[l][r] + 1, r);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);

    // 遍历区间长度
    for (int len = 1; len <= n; len++) {
        // 遍历左端点
        for (int l = 1; l <= n - len + 1; l++) {

            int r = l + len - 1;        // 右端点

            // 遍历根节点
            for (int k = l; k <= r; k++) {
                if (l == r) {
                    f[l][r] = w[l];     // 叶节点
                    root[l][r] = l;     
                } else {
                    int left_score = l == k ? 1 : f[l][k - 1];
                    int right_score = r == k ? 1 : f[k + 1][r];
                    int score = left_score * right_score + w[k];    // 当前二叉树分值
                    if (f[l][r] < score) {
                        f[l][r] = score;        // 更新得分
                        root[l][r] = k;         // 更新根节点
                    }

                }
            }
        }
    }

    cout << f[1][n] << endl;

    dfs(1, n);

    return 0;
}

AcWing 1414. 牛异或

思路：

用前缀和思想，把寻找最优连续子数组问题转换成寻找两个数的问题，进而可用最大异或对解决

令s[i]表示$A_1 \oplus A_2 \oplus \cdots \oplus A_i$，即异或前缀和

用字典树存储s[1]~s[n]，即所有异或前缀和。字典树查找效率为$O(\log21)$，是常数级别，因此相比朴素算法效率更高，可将时间复杂度$O(n^2)$优化成$O(n\log21) \approx O(n)$

为了让右端点最小，可让左端点最大。

代码实现：

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, son[N * 21][2], id[N * 21], idx, s[N];

void insert(int x, int k) {
    int p = 0;
    for (int i = 20; i >= 0; i--) {
        int u = x >> i & 1;
        if (!son[p][u]) son[p][u] = idx++;
        p = son[p][u];
    }
    id[p] = k;      // 保证左端点最大，进而保证右端点最小
}

int query(int x) {
    int p = 0;
    for (int i = 20; i >= 0; i--) {
        int u = x >> i & 1;
        if (son[p][!u]) p = son[p][!u];
        else p = son[p][u];
    }
    return id[p];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &s[i]);
        s[i] ^= s[i - 1];
    }

    int res = -1, a = -1, b = -1;
    insert(s[0], 0);
    for (int i = 1; i <= n; i++) {
        // 异或前缀和
        int k = query(s[i]);    // 在异或树查找当前最优的异或前缀和位置
        int tmp = s[i] ^ s[k];  // 计算当前最优结果s_{k+1} ^ s_{k+2} ^ ... ^ s_i
        if (res < tmp) {
            res = tmp;          // 保存结果
            a = k + 1;          // 注意计算的下标是从k+1起
            b = i;
        }
        insert(s[i], i);
    }

    printf("%d %d %d\n", res, a, b);

    return 0;
}

Week2

AcWing 1230. K倍区间

思路：

由前缀和定义得：
$$ a_i+a_{i+1}+\cdots +a_j=S_j-S_{i-1} $$
由：
$$ (S_j-S_{i-1})\,\,\mathrm{mod} \,\,k\,\,=\,\,0 $$
可得：
$$ S_j\,\, \mathrm{mod} \,\,k\,\,=S_{i-1}\,\,\mathrm{mod} \,\,k\,\, $$
因此只需统计前缀和$S_i$模$k$相等的个数，从中任选两个都能满足上述等式。例如$S_2 \mod \,\,k=S_3 \mod \,\,k=S_5 \mod \,\,k=3$，即数组只有$S_2$、$S_3$和$S_5$这三个前缀和模$k$余$3$，故从中任选2个都能满足上述等式，共有$C_{3}^{2}=3$中情况。同理，把模$k$余$0$，余$1$，…，余$k-1$分别按类似之前的方式处理，求和即可得到结果。

注意要单独处理$S_0 \mod k=0 $的情况，由于$S_0=0$，故只需让cnt[0]++，这是为了防止漏掉$a_1+a_2+ \cdots + a_n=S_n-S_0$的情况

前缀和可把时间复杂度从$O(n^2)$降到$O(n)$，采用哈希表存储区间模k取余的个数，例如区间求和模k余3，这a[3]++

代码实现：

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
int n, k, cnt[N];
LL s[N];

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &s[i]);
        s[i] += s[i - 1];       // 转换成前缀和
    }

    // 对前缀和模k取余情况分组
    cnt[0]++;       // s[0] % k = 0
    for (int i = 1; i <= n; i++) 
        cnt[s[i] % k]++;   

    // 分别处理余数不同的情况
    LL res = 0;
    for (int i = 0; i <= k - 1; i++) 
        res += (LL) cnt[i] * (cnt[i] - 1) / 2;  // C_2^n

    cout << res << endl;

    return 0;
}

AcWing 1613. 数独简单版

思路：

用三个布尔数组row[N][N]、col[N][N]和cell[3][3][N]判断方案是否可行，可用x / 3，y / 3表示小方格坐标（注意这里是整数除法）。

其中row[x][k]为true表示第x行已经存在数字k，同理col[y][k]为true表示第y列已经存在数字k，cell[x / 3][y / 3][k]为true表示第x行第y列方格所在的块已经存在数字k。

借助DFS遍历所有情况。

代码实现：

#include <iostream>
using namespace std;
const int N = 10;
bool row[N][N], col[N][N], cell[3][3][N];
char g[N][N];

bool dfs(int x, int y) {
    if (y == 9) {
        x++;
        y = 0;
    }
    if (x == 9) {
        // 找到结果
        for (int i = 0; i < 9; i++) puts(g[i]);
        return true;
    }

    if (g[x][y] != '.') {
        return dfs(x, y + 1);     // 已经填有数字
    } 

    for (int k = 1; k <= 9; k++) {
        if (!row[x][k] && !col[y][k] && !cell[x / 3][y / 3][k]) {
            g[x][y] = (char)('0' + k);
            row[x][k] = col[y][k] = cell[x / 3][y / 3][k] = true;
            if (dfs(x, y + 1)) return true;     // 修枝
            row[x][k] = col[y][k] = cell[x / 3][y / 3][k] = false;
            g[x][y] = '.';
        }
    }
    return false;
}

int main() {
    for (int i = 0; i < 9; i++) cin >> g[i];

    // 预处理
    for (int x = 0; x < 9; x++)
        for (int y = 0; y < 9; y++)
            if (g[x][y] != '.') {
                int t = g[x][y] - '0';
                row[x][t] = true;
                col[y][t] = true;
                cell[x / 3][y / 3][t] = true;
            }


    dfs(0, 0);

    return 0;
}

AcWing 122. 糖果传递

思路：

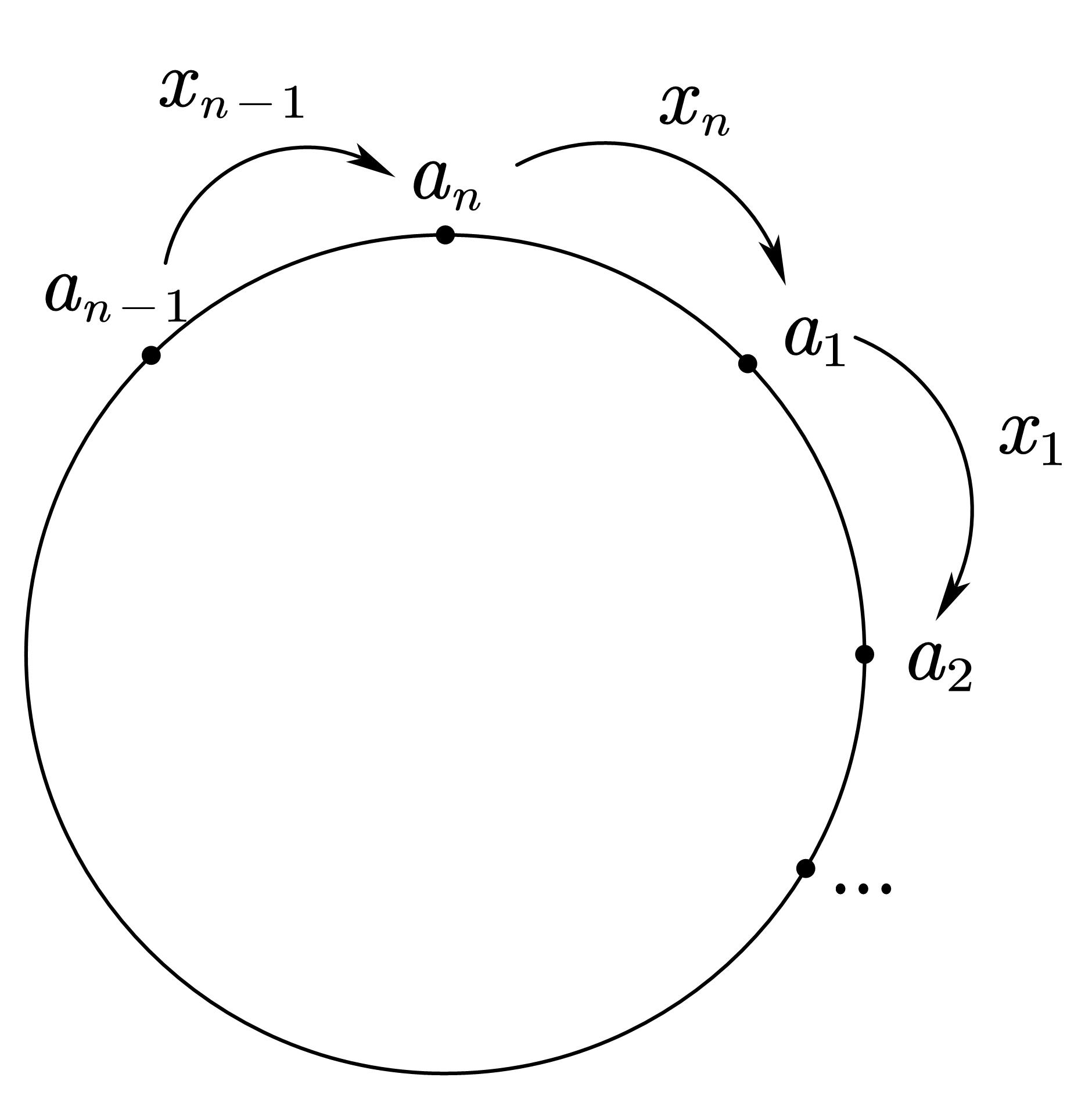
假设$n$个小朋友分别为$a_1, a_2,\cdots,a_n$，小朋友$a_k$给小朋友$a_{k+1}$的糖果数为$x_k$，若$x_k<0$，则表示小朋友$a_{k+1}$给小朋友$a_k$了$|x_k|$个糖果。

令
$$ b = \frac{a_1+ a_2+\cdots+a_n}{n} $$
则最后所有小朋友手中的糖果数应为$b$，目标函数为：
$$ \min \left| x_1 \right|+\left| x_2 \right|+\cdots +\left| x_n \right| $$
由题意知：
$$ \begin{cases} a_1-x_1+x_n=b\\\ a_2-x_2+x_1=b\\\ \cdots\\\ a_n-x_n+x_{n-1}=b\\\ \end{cases} $$
化简得：
$$ \begin{cases} x_1=x_n-\left( b-a_1 \right)\\\ x_2=x_n-\left( 2b-a_1-a_2 \right)\\\ \cdots\\\ x_{n-1}=x_n-\left( \left( n-1 \right) b-a_1-a_2-\cdots -a_{n-1} \right)\\\ x_n=x_n-\left( nb-a_1-a_2-\cdots -a_{n-1}-a_n \right) =x_n-0\\\ \end{cases} $$
故目标函数可化为
$$ \left| x_n-\left( b-a_1 \right) \right|+\left| x_n-\left( 2b-a_1-a_2 \right) \right|+\cdots +\left| x_n-\left( \left( n-1 \right) b-a_1-a_2-\cdots -a_{n-1} \right) \right|+\left| x_n-0 \right| $$
令$x=x_n$，$c_k=kb-\sum_{i=1}^k{a_i}$，则目标函数可简化成
$$ \left| x-c_1 \right|+\left| x-c_2 \right|+\cdots +\left| x-c_n \right| $$
此时问题变成货仓选址问题，可用排序不等式求解，即让$x$取数组$\{c_k\}$的中位数即可

考虑最优解$\{x_1, x_2,\cdots,x_n\}$的构成，它不可能全是正数。反证法：假设$\forall i, x_i>0$，且$x_k$是最小值，令所有$x_i$都减去$x_k$，则可得到比最优解更好的解，矛盾。同理它也不可能全是负数。故最优解一定由一些大于0和一些不大于0的$x_i$组成，不妨设$x_{k} >0$且$x_{k+1} \leqslant 0$，即$a_k$是一个只给不拿的小朋友。

算法思路：

if (x[k] >= 0) {
    // 立即给
    a[k + 1] += x[k];
    dfs(k + 1);
} else {
    // 最后才给
    dfs(k + 1);
    a[k] += x[k];
}

代码实现：

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int n, a[N];
LL c[N];

int main() {
    cin >> n;

    LL b = 0;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        b += a[i];
    }
    b /= n;     // 平均值

    // 求参数c
    for (int i = 1; i <= n; i++) c[i] = c[i - 1] + b - a[i];

    nth_element(c + 1, c + (n + 1) / 2, c + n + 1);     // c[0]不是有效数
    int middle = c[(n + 1) / 2];

    LL cost = 0;
    for (int i = 1; i <= n; i++) cost += abs(middle - c[i]);

    cout << cost << endl;

    return 0;
}

AcWing 125. 耍杂技的牛

思路：

算法基础课——耍杂技的牛

难点在于证明贪心算法

代码实现：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e4 + 10;

typedef pair<int, int> PII;
typedef long long LL;
PII cows[N];

int main() {
    int n;
    cin >> n;

    int w, s;
    for (int i = 0; i < n; i++) {
        scanf("%d%d", &w, &s);
        cows[i] = {w + s, s};
    }

    sort(cows, cows + n);   // 按w + s排序

    LL sum = 0, res = -2e9;
    for (int i = 0; i < n; i++) {
        s = cows[i].second;
        w = cows[i].first - s;
        res = max(res, sum - s);        // 注意与后一行的顺序
        sum += w;
    }

    cout << res << endl;

    return 0;
}