AcWing《寒假每日一题(入门组)》笔记
持续更新中…
Week01
AcWing 104. 货仓选址
思路
问题可转化成
max{|a1−x|+|a2−x|+⋯+|an−x|}≥|an−a1|+|an−1−a2|+⋯
当n为奇数时,x取中位数;当n为偶数时,x取两个中位数之间的任何数;
此时绝对值不等式取等号
代码实现时,可选两个中位数较大的一个,即右边界,保证不等式取等号
代码实现
方法1
直接按思路实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int main() {
cin >> n;
for (int i = 0; i < n; i ++) cin >> a[i];
sort(a, a + n);
long res = 0;
for (int i = 0 ; i < n; i++ ) res += abs(a[i] - a[n / 2]); \\ 取右边界
cout << res << endl;
return 0;
}
思路2
可以用ai−ai/2代替|ai−an/2|
二者求和展开后是一样的
而前者可以省去求绝对值的过程,速度更快
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
long res = 0;
for (int i = 0; i < n; i++) res += a[i] - a[i / 2];
cout << res << endl;
return 0;
}
方法3
题目实际上并不需要所有位置的确切位置,只需要知道中位数就行
因此可通过库函数nth_element()直接计算中位数,实际上它可以在O(n)时间计算任何第k大的数,见算法基础班的求第k个数
此时算法时间复杂度由O(nlogn)降为O(n)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
nth_element(a, a + n / 2, a + n);
long res = 0;
for (int i = 0; i < n; i++) res += abs(a[i] - a[n / 2]);
cout << res << endl;
return 0;
}
拓展
本题是一维情形,当扩展到二维时,可用三分求解;当扩展到十维以上时,需要用模拟退火算法求解
AcWing 898. 数字三角形
思路:
算法基础课——数字三角形
代码实现:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n, a[N][N], f[N][N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
scanf("%d", &a[i][j]);
memset(f, 0x80, sizeof f); // 0x80808080作为无穷小
f[1][1] = a[1][1];
for (int i = 2; i <= n; i++)
for (int j = 1; j <= i; j++)
f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
int res = -2e9;
for (int j = 1; j <= n; j++) res = max(res, f[n][j]);
cout << res << endl;
return 0;
}
Week2
AcWing 756. 蛇形矩阵
思路:
可按”右→下→左→上”循环,直至走过的步数等于矩阵元素个数。
右:{0, 1}
下:{1, 0}
左:{0, -1}
上:{-1, 0}
代码实现:
#include <iostream>
using namespace std;
const int N = 103;
int n, m, a[N][N];
void print() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++)
printf("%d ", a[i][j]);
puts("");
}
}
void fun() {
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
int d = 0; // 当前方向
int res = 1, x = 0, y = 0;
a[x][y] = res++;
while(res <= n * m) {
int new_x = x + dx[d], new_y = y + dy[d];
if (new_x < 0 || new_x >= n || new_y < 0 || new_y >= m || a[new_x][new_y]) {
d = (d + 1) % 4; // 撞墙或已经写过,改变方向
} else {
a[new_x][new_y] = res++;
x = new_x;
y = new_y;
}
}
}
int main() {
cin >> n >> m;
fun();
print();
return 0;
}
AcWing 1113. 红与黑
思路:
Flood Fill算法(洪水灌溉算法)
本质是网格搜索问题,可用BFS或DFS解决
代码实现:
代码实现1:BFS
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
const int N = 23, M = 23;
char board[N][M];
int n, m;
typedef pair<int, int> PII;
int bfs(int begin, int end) {
queue<PII> q;
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
board[begin][end] = '#';
q.push({begin, end});
int res = 0;
while(q.size()) {
PII temp = q.front();
q.pop();
res++;
int x = temp.first, y = temp.second;
for (int d = 0; d < 4; d++) {
int new_x = x + dx[d], new_y = y + dy[d];
if (new_x >= 0 && new_x < n && new_y >= 0 && new_y < m && board[new_x][new_y] == '.') {
board[new_x][new_y] = '#';
q.push({new_x, new_y});
}
}
}
return res;
}
int main() {
while(cin >> m >> n, m, n) {
for (int i = 0; i < n; i++) cin >> board[i];
int begin = 0, end = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (board[i][j] == '@') {
begin = i;
end = j;
}
cout << bfs(begin, end) << endl;
}
return 0;
}
代码实现2:DFS
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
const int N = 23, M = 23;
char board[N][M];
int n, m;
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
int dfs(int x, int y) {
int res = 1;
for (int d = 0; d < 4; d++) {
int new_x = x + dx[d], new_y = y + dy[d];
if (new_x >= 0 && new_x < n && new_y >= 0 && new_y < m && board[new_x][new_y] == '.') {
board[new_x][new_y] = '#';
res += dfs(new_x, new_y);
}
}
return res;
}
int main() {
while(cin >> m >> n, m, n) {
for (int i = 0; i < n; i++) cin >> board[i];
int begin = 0, end = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (board[i][j] == '@') {
begin = i;
end = j;
}
cout << dfs(begin, end) << endl;
}
return 0;
}
AcWing 1346. 回文平方
思路:
b进制转换成十进制:
n=akbk+ak−1bk−1+⋯+a0
因此a_0=n \mod b,由于
\lfloor \frac{n}{b} \rfloor = a_k b^{k-1} + a_{k-1}b^{k-2}+\cdots + a_1
若让n变成\lfloor \frac{n}{b} \rfloor,则a_1 = n \mod b
同理,可通过迭代获得a_ka_{k-1}\cdots a_0
最后只需转换成字符串,用双指针判断是否是回文数即可。
代码实现:
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int b;
char get(int k) {
if (k <= 9) return (char)('0' + k);
else return (char)('A' + k - 10);
}
string base(int x) {
string str;
while(x) {
str += get(x % b);
x /= b;
}
reverse(str.begin(), str.end());
return str;
}
bool check(string str) {
for (int i = 0, j = str.size() - 1; i < j; i++, j--)
if (str[i] != str[j]) return false;
return true;
}
int main() {
cin >> b;
for (int i = 1; i <= 300; i++) {
string str = base(i * i);
if (check(str)) cout << base(i) << " " << str << endl;
}
return 0;
}
AcWing 680. 剪绳子
思路:
本质是浮点数二分查找,即在(0, \text{max_length}]查找满足下式且满足精度的最大mid \sum_{i=0}^{n-1}{\lfloor \frac{L_i}{mid} \rfloor } \geqslant k mid可通过mid = (l + r) / 2.0$计算
① 当mid满足条件时,则在[mid, r]继续查找,即让l = mid;
② 当mid不满足条件时,则在[l, mid]继续查找,即让r = mid;
代码实现:
#include <iostream>
#include <cmath>
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-4;
int n, k;
int L[N];
bool check(double mid) {
int res = 0;
for (int i = 0; i < n; i++)
res += floor((double) L[i] / mid);
return res >= k;
}
int main() {
cin >> n >> k;
for (int i = 0; i < n; i++) scanf("%d", &L[i]);
double l = 0.0, r = 1e9;
while(r - l > eps) {
double mid = (l + r) / 2.0;
if (check(mid)) l = mid;
else r = mid;
}
printf("%.2f\n", r);
return 0;
}
AcWing 1227. 分巧克力
思路:
实际上在[0, \text{max_length}]查找满足下式条件的最大的mid,可用二分查找。假设mid满足条件,则由下式知,[1, mid]都会满足条件。
\sum_{i=0}^{n-1}{\lfloor \frac{h_i}{mid} \rfloor \cdot}\lfloor \frac{w_i}{mid} \rfloor \geqslant k
① 当mid满足条件时,需要在[mid, r]搜索,即l = mid;
② 当mid不满足条件时,需要在[l, mid - 1]搜索,即r = mid - 1;
此时二分模板里的mid应当用mid = l + r + 1 >> 1计算
代码实现:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
int n, k, h[N], w[N];
bool check(int mid) {
LL sum = 0;
for (int i = 0; i < n; i++)
sum += LL(h[i] / mid) * (w[i] / mid);
return sum >= k;
}
int main() {
cin >> n >> k;
for (int i = 0; i < n; i++) scanf("%d%d", &h[i], &w[i]);
int l = 1, r = 1e5;
while (l < r) {
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
cout << l << endl;
return 0;
}
AcWing 422. 校门外的树
思路:
算法基础课——区间合并
合并要被砍掉的区间,然后用总数相减即可
代码实现:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
vector<PII> seg;
int main() {
int n, m;
cin >> n >> m;
int l, r;
while(m--) {
scanf("%d %d", &l, &r);
seg.push_back({l, r});
}
sort(seg.begin(), seg.end());
int a = -1, b = -1, res = 0;
for (PII term : seg) {
int x = term.first, y = term.second;
if (x < b) b = max(b, y);
else {
if (b != -1) res += b - a + 1;
a = x;
b = y;
}
}
res += b - a + 1;
cout << (n - res + 1) << endl;
return 0;
}
AcWing 429. 奖学金
思路:
考察多关键字排序,重载小于号即可
代码实现:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
struct Student {
int id, sum, a, b, c;
bool operator<(const Student& stu) const {
if (sum != stu.sum) return sum > stu.sum;
else if (a != stu.a) return a > stu.a;
else return id < stu.id;
}
} stu[N];
int main() {
int n, a, b, c;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a >> b >> c;
stu[i] = {i, a + b + c, a, b, c};
}
sort(stu + 1, stu + n + 1);
for (int i = 1; i <= 5; i++) printf("%d %d\n", stu[i].id, stu[i].sum);
return 0;
}
Week3
AcWing 1208. 翻硬币
思路:
题目性质:
① 操作顺序无影响
② 影响最多1次
从左到右遍历,不同则翻转,直到末尾,即可得到最少次数(贪心)
代码实现:
#include <iostream>
using namespace std;
const int N = 110;
char s1[N], s2[N];
void turn(char s[], int k) {
if (s[k] == '*') s[k] = 'o';
else s[k] = '*';
}
int main() {
cin >> s1 >> s2;
int res = 0;
for (int i = 0; s1[i + 1]; i++)
if (s1[i] != s2[i]) {
turn(s1, i);
turn(s1, i + 1);
res ++;
}
cout << res << endl;
return 0;
}
AcWing 1532. 找硬币
思路:
思路1:
借助哈希表加快查询,但要注意哈希表unordered_set不能获得重复元素的个数,因此不能先全部插入哈希表,再调用算法查询,而是要边读取边插入,而且先判断再插入,从而解决需要两个相同硬币的情况。
思路2:
算法基础课——双指针法
需要排序
代码实现:
方法1:哈希表
#include <iostream>
#include <unordered_set>
using namespace std;
const int N = 1e5 + 10, INF = 1010;
int n, m;
unordered_set<int> h;
int main() {
cin >> n >> m;
int v1 = INF, v2 = INF;
for (int i = 0; i < n; i++) {
int x, y;
scanf("%d", &x);
y = m - x;
if (h.count(y)) {
if (x > y) swap(x, y);
if (x < v1) {
v1 = x;
v2 = y;
}
}
h.insert(x);
}
if (v1 == INF) puts("No Solution");
else printf("%d %d\n", v1, v2);
return 0;
}
方法2:双指针
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, m, a[N];
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
sort(a, a + n);
for (int i = 0, j = n - 1; i < j; i++) {
while(i < j && a[i] + a[j] > m) j--;
if (i < j && a[i] + a[j] == m) {
if (a[i] > a[j]) swap(a[i], a[j]);
printf("%d %d\n", a[i], a[j]);
return 0;
}
}
puts("No Solution");
return 0;
}
AcWing 1341. 十三号星期五
思路:
思路1:基姆拉尔森计算公式
把1月和2月看成13月和14月,则可按下式计算某天是星期几
W = (d + 2 * m + 3 * (m + 1) / 5 + y + y / 4 - y / 100 + y / 400 + 1) % 7
思路2:枚举
枚举每月第1天距离1990-01-01过了多少天,注意闰年判别即可
代码实现:枚举法
#include <iostream>
using namespace std;
int month_Days[2][13] = {
{0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31},
{0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31} // 闰年
};
int weekDays[7];
int main() {
int n;
cin >> n;
int Days = 0;
for (int year = 1900; year < 1900 + n; year++) {
bool flag = (year % 4 == 0 && year % 100 != 0) || year % 400 == 0;
for (int month = 1; month <= 12; month++) {
weekDays[(Days + 12) % 7]++;
Days += month_Days[flag][month];
}
}
for (int i = 0, k = 5; i < 7; i++, k = (k + 1) % 7) printf("%d ", weekDays[k]);
puts("");
return 0;
}
AcWing 754. 平方矩阵 II
思路:
第i行第j列的元素值为|i - j| + 1
代码实现:
#include <iostream>
using namespace std;
int main() {
int n;
while(cin >> n, n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
printf("%d ", abs(i - j) + 1);
printf("\n");
}
printf("\n");
}
return 0;
}
AcWing 1432. 棋盘挑战
思路:
算法基础课笔记——n-皇后问题
代码实现:
#include <iostream>
using namespace std;
const int N = 15;
bool col[N], dg[2 * N], udg[2 * N];
int n, path[N], res;
void dfs(int i) {
if (i > n) {
res++;
if (res <= 3) {
for (int k = 1; k <= n; k++) printf("%d ", path[k]);
puts("");
}
return;
}
for (int j = 1; j <= n; j ++)
if (!col[j] && !dg[i + j] && !udg[i - j + n]) {
path[i] = j;
col[j] = dg[i + j] = udg[i - j + n] = true;
dfs(i + 1);
col[j] = dg[i + j] = udg[i - j + n] = false;
}
}
int main() {
cin >> n;
dfs(1);
cout << res << endl;
return 0;
}
AcWing 1371. 货币系统
思路:
问题等价于完全背包问题,在基础班里求的属性是最大值,而在这求的是数量,即总方案数
假设状态f(i,j)表示所有满足从1~i中选且总钱数为j的方案集合,属性为数量。
由于第i种货币至多能选\lfloor \frac{j}{v_i} \rfloor个,可按第i种货币选择的数量分类:
当选择0个时,方案数为f(i-1,j)
当选择1个时,方案数为f(i-1,j-v_i)
当选择2个时,方案数为f(i-1,j-2v_i)
\cdots
当选择\lfloor \frac{j}{v_i}\rfloor个时,方案数为f(i-1,j-\lfloor \frac{j}{v_i} \rfloor v_i)
因此有
f\left( i,j \right) =f\left( i-1,j \right) +f\left( i-1,j-v_i \right) +f\left( i-1,j-2v_i \right) +\cdots +f\left( i-1,j-\lfloor \frac{j}{v_i} \rfloor v_i \right)
由于
f\left( i,j-v_i \right) =f\left( i-1,j-v_i \right) +f\left( i-1,j-2v_i \right) +\cdots +f\left( i-1,j-\lfloor \frac{j}{v_i} \rfloor v_i \right)
故可得状态转移方程:
f\left( i,j \right) =f\left( i-1,j \right) +f\left( i,j-v_i \right)
题目所求答案为f(v,n)
代码实现:
方法1(未优化空间):
#include <iostream>
using namespace std;
const int N = 28, M = 1e4 + 10;
typedef long long LL;
int n, m;
int weight[N];
LL f[N][M];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) scanf("%d", &weight[i]);
f[0][0] = 1; // 钱数为0的方案为不选,也是合法方案
for (int i = 1; i <= n; i++) {
int w = weight[i];
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if (j >= w)
f[i][j] += f[i][j - w];
}
}
cout << f[n][m] << endl;
return 0;
}
方法2(优化空间):
#include <iostream>
using namespace std;
const int N = 28, M = 1e4 + 10;
typedef long long LL;
int n, m;
int weight[N];
LL f[M];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) scanf("%d", &weight[i]);
f[0] = 1; // 钱数为0的方案为不选,也是合法方案
for (int i = 1; i <= n; i++) {
int w = weight[i];
for (int j = w; j <= m; j++)
f[j] += f[j - w];
}
cout << f[m] << endl;
return 0;
}
说明:
- 矩阵
f的边界分析- ①
f[0][0]表示从空集构造0元的方案数,显然什么都不拿就可满足,此时方案数为1 - ② 当
j > 0时,f[0][j]表示从空集构造j元的方案数,显然这不可能存在,故方案数都为0,即默认值 - ③ 当
i > 0时,f[i][0]表示从第1~i种货币构造0元的方案数,显然什么都不拿就可满足,此时方案数为1
- ①
- 边界条件①需要手动声明,边界条件②只需用默认值,边界条件③可通过内层循环计算
j = 0的情况保证
AcWing 1381. 阶乘
题意:
求n!右起第1个非0数字
思路:
由质因数分解定理知,n!可按下式分解
n!=2^{\alpha}5^{\beta}p_{1}^{\gamma_1}p_{2}^{\gamma_2}\cdots p_{m}^{\gamma_m}
由于质因子p_i^{\alpha_i}的指数\alpha_i可通过下式求解
\alpha_i=\lfloor \frac{n!}{p_i} \rfloor +\lfloor \frac{n!}{p_{i}^{2}} \rfloor +\lfloor \frac{n!}{p_{i}^{3}} \rfloor +\cdots
显然质因子2的指数比质因子5的指数大,因为由上式知,质因子2的指数计算公式不仅项数多,而且每一项都比质因子5的大,故有\alpha \geqslant \beta
假设k表示n!末尾0的个数,则问题等价于求
\frac{n!}{10^k}\,\,\mathrm{mod} 10
由于\alpha \geqslant \beta,则\min \left\{ \alpha ,\beta \right\} =\beta ,故k = \beta,因此
\frac{n!}{10^k}\,\,\mathrm{mod}10=\frac{n!}{2^k5^k}\,\,\mathrm{mod}1
\\
=2^{\alpha-k}5^{\beta -k}p_{1}^{\gamma_1}p_{2}^{\gamma_2}\cdots p_{m}^{\gamma_m}\,\,\mathrm{mod}10
\\
=2^{\alpha -\beta}p_{1}^{\gamma_1}p_{2}^{\gamma_2}\cdots p_{m}^{\gamma_m}\,\,\mathrm{mod}10
若令\mathrm{res}=p_{1}^{\gamma_1}p_{2}^{\gamma_2}\cdots p_{m}^{\gamma_m}\,\,\mathrm{mod}10,则n!=2^{\alpha}5^{\beta}\mathrm{res}。用试除法求得\alpha和\beta后,可得到\mathrm{res},然后计算2^{\alpha-\beta}\mathrm{res}\,\,\mathrm{mod}10即可得到答案。
时间复杂度:
试除法计算当前数的\alpha和\beta的时间复杂度是O(\log n),因此计算阶乘(n个数)的时间复杂度是O(n \log n)
代码:
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
int res = 1; // 非0末尾数
int d2 = 0, d5 = 0; // 质因子指数
for (int i = 1; i <= n; i++) {
int x = i; // 备份,不能改变变量i
// 求质因子2的指数
while (x % 2 == 0) {
x /= 2;
d2++;
}
// 求质因子5的指数
while (x % 5 == 0) {
x /= 5;
d5++;
}
res = res * x % 10;
}
for (int i = 0; i < d2 - d5; i++) {
res = res * 2 % 10;
}
printf("%d\n", res);
return 0;
}
拓展题目:
Week4
AcWing 1353. 滑雪场设计
思路:
一共有84个可能的区间:[0, 17], [1, 18], …, [83, 100],不存在[-1, 16]等这样的区间,因为假设这是最优区间,则可以证明[0, 17]
比它花费更少,矛盾;同理也不存在[84, 101]这样的区间。
因此只需枚举所有区间即可。
也可证明代价函数是凸函数(用二阶导数证明),然后用三分求解。
代码实现:
#include <iostream>
using namespace std;
const int N = 1010, INF = 2e9;
int n, h[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) scanf("%d", &h[i]);
int min_cost = INF;
for (int i = 0; i <= 100 - 17; i++) {
int cost = 0, l = i, r = i + 17;
for (int j = 0; j < n; j++)
if (h[j] < l) cost += (l - h[j]) * (l - h[j]);
else if (h[j] > r) cost += (h[j] - r) * (h[j] - r);
if (cost < min_cost) min_cost = cost;
}
cout << min_cost << endl;
return 0;
}
AcWing 1603. 整数集合划分
思路:
当n为奇数时,n_1取\lfloor \frac{n}{2} \rfloor,n_2取\lfloor \frac{n}{2} \rfloor + 1,此时|n_1 - n_2|=0
当n为偶数时,n_1取\lfloor \frac{n}{2} \rfloor,n_2也取\lfloor \frac{n}{2} \rfloor,此时|n_1 - n_2|=1
当x_1,x_2,\cdots,x_n为单调序列,S_1为前\lfloor \frac{n}{2} \rfloor个,S_2为剩余元素时,|S_2-S_1|最大。证明如下:
\forall x_1\in S_1, \forall x_2\in S_2,交换二者,则S_1变成S_1 - x_1 + x_2,S_2变成S_2 - x_2 + x_1,后者减去前者可得S_2 - S_1 - 2(x_2-x_1)。由于S_2 \geqslant S_1且x_2 \geqslant x_1,故S_2 - S_1 - 2(x_2-x_1) \leqslant S_2 - S_1,即交换后二者之差不超过原来的差值,故原来为最优的情况。
代码实现:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, a[N];
int main() {
cin >> n;
for (int i = 0; i < n; i ++) scanf("%d", &a[i]);
sort(a, a + n);
int s1 = 0, s2 = 0;
for (int i = 0; i < n / 2; i ++) s1 += a[i];
for (int i = n / 2; i < n; i ++) s2 += a[i];
printf("%d %d\n", n % 2, s2 - s1);
return 0;
}
AcWing 482. 合唱队形
思路:
算法提高课——合唱队型
代码实现:
#include <iostream>
using namespace std;
const int N = 105;
int n, a[N], f[N], g[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
for (int i = 0; i < n; i++) {
f[i] = 1;
for (int j = 0; j < i; j++)
if (a[i] > a[j])
f[i] = max(f[i], f[j] + 1);
}
for (int i = n - 1; i >= 0; i--) {
g[i] = 1;
for (int j = n - 1; j > i; j--)
if (a[i] > a[j])
g[i] = max(g[i], g[j] + 1);
}
int res = 0;
for (int i = 0; i < n; i++) res = max(res, f[i] + g[i] - 1);
cout << n - res << endl;
return 0;
}
AcWing 420. 火星人
思路:
可通过库函数next_permutation()获取下一个排列(从小到大的顺序)
或自己实现库函数,例如1 3 5 4 2的下一个排列是1 4 2 3 5
① 从右往左找到第1个逆序数(改变单调性的数),在例子中是3,因为2 4 5单调递增,而2 4 5 3不递增(无单调性)
② 在这个数右边的数中寻找一个数x,使得x比它大且最小。在这里是4,因为只有4和5比3大,且4是最小的那个。
③ 交换这两个数,得到1 4 5 3 2,此时得到以1 4开头最大的数,因为后边的数是单调递减的。
④ 翻转1 4之后的数,即可得到下一个数1 4 2 3 5,因为后边的数是单调递增的
笔记:
- 单调递增时,数最小
- 单调递减时,数最大
代码实现:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010;
int a[N];
int n, m;
void next_perm() {
int k = n - 1;
while(k >= 0 && a[k - 1] > a[k]) k--;
int t = k + 1;
while(t < n && a[k - 1] < a[t]) t++;
swap(a[k - 1], a[t - 1]);
reverse(a + k, a + n);
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
while(m--) next_perm();
for(int i = 0; i < n; i++)
printf("%d ", a[i]);
return 0;
}
AcWing 1015. 摘花生
思路:
算法提高课——摘花生
代码实现:
#include <iostream>
using namespace std;
const int N = 104;
int a[N][N], f[N][N];
int main() {
int n, r, c;
cin >> n;
while(n--) {
cin >> r >> c;
for (int i = 1; i <= r; i++)
for (int j = 1; j <= c; j++)
scanf("%d", &a[i][j]);
for (int i = 1; i <= r; i++)
for (int j = 1; j <= c; j++)
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j];
cout << f[r][c] << endl;
}
return 0;
}
AcWing 126. 最大的和
思路:
直接用二维前缀和时间复杂度是O(n^4),可优化成O(n^3):即不用左边界,而只用右边界k
一维情况:
假设f[k]表示以a[k]结尾的最大连续子序列和,则有f[k+1]=max(f[k], 0) + a[k+1]。当f[k]<=0时,最大连续子序列应为a[k+1]自身;否则为二者的和。
算法大致思路:
① 读入数据,计算每一列的前缀和,此时g[i][j]表示第j列a[1][j]+a[2][j]+...+a[i][j]的和
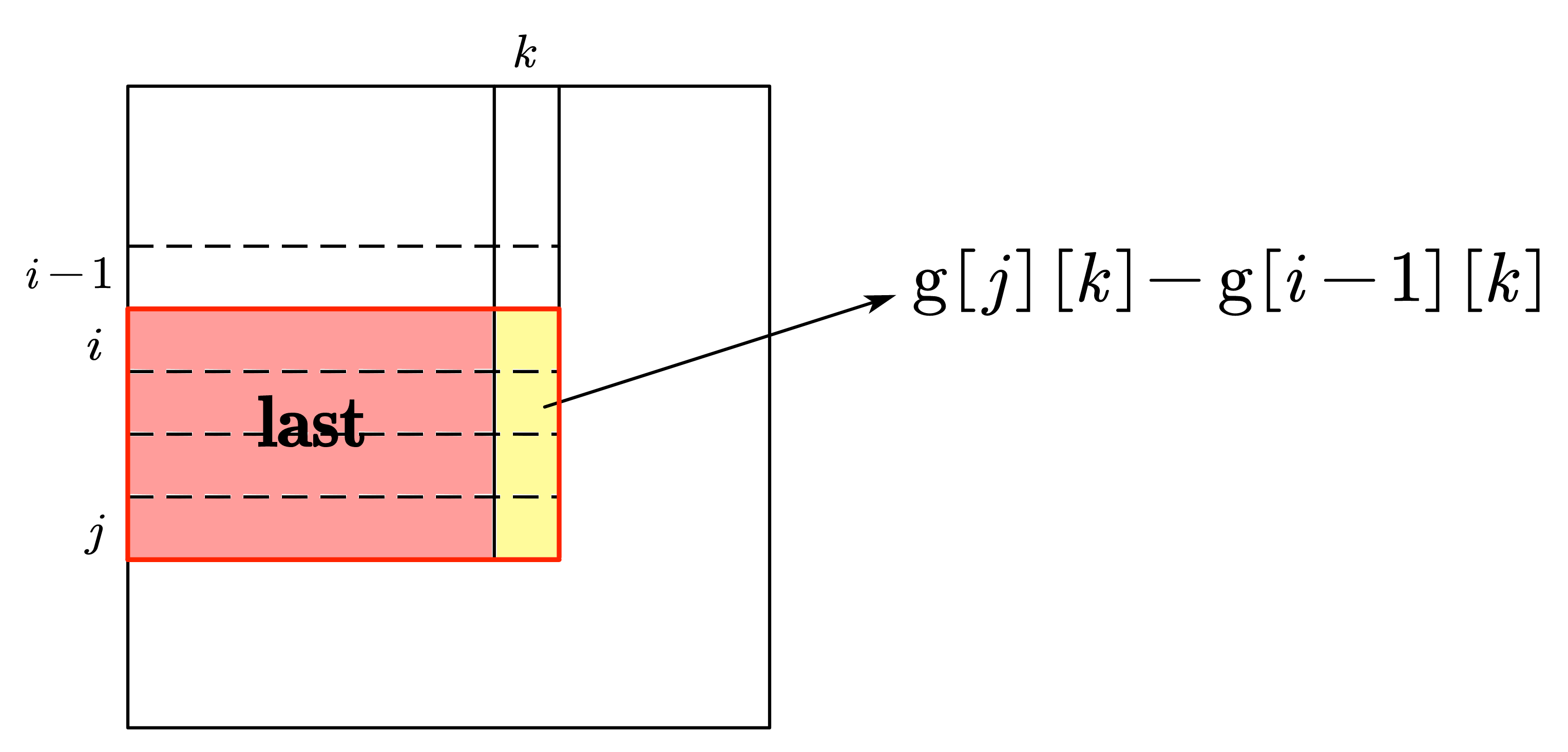
② 假设i表示上边界,j表示下边界,k表示右边界,则g[i][j]表示以i为上边界,j为下边界的子矩阵中,最大的子矩阵和。
③ 假设last表示以i为上边界,j为下边界,k-1为右边界的子矩阵中,最大的子矩阵和,则有递推关系g[i][j] = max(last, 0) + g[j][k] - g[i - 1][k]
④ 在迭代时,最大的last即为子矩阵中最大的和
代码实现:
#include <iostream>
using namespace std;
const int N = 104;
int n, g[N][N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j ++) {
cin >> g[i][j];
g[i][j] += g[i - 1][j]; // 转换成每一列的前缀和
}
int res = -2e9; // 保存所有子矩阵中最大的和
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j ++) {
int last = 0;
for (int k = 1; k <= n; k++) {
// 以i为上边界,j为下边界,k为右边界的子矩阵集合中,最大的和
last = max(last, 0) + g[j][k] - g[i - 1][k];
res = max(res, last); // 更新最大值
}
}
cout << res << endl;
}
Week5
AcWing 426. 开心的金明
思路:
实际上是01背包问题,只是这里的重量=价格,价值=价格×重要度
代码实现:
未压缩(二维):
#include <iostream>
using namespace std;
const int N = 30, M = 30010;
int m, n, v[N], w[N], f[N][M];
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i++) {
scanf("%d%d", &v[i], &w[i]);
w[i] *= v[i]; // 价值 = 价格×重要度
}
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if (j >= v[i])
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
压缩(一维):
#include <iostream>
using namespace std;
const int N = 30, M = 30010;
int m, n, v[N], w[N], f[M];
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i++) {
scanf("%d%d", &v[i], &w[i]);
w[i] *= v[i]; // 价值 = 价格×重要度
}
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}
AcWing 703. 数独检查
思路:
依次检查行、列、方格即可。方格可通过二重循环偏移量dx和dy实现。
注意题目没说一定是9宫格,事实上是n^2宫格,因此需要注意读入过程。
方格循环里有很多坑:
- 步长变化是
x += n,而不是x++ memset()在第2层循环里,而不是像其它两个check在第1层循环里
代码实现:
#include <iostream>
#include <cstring>
using namespace std;
const int M = 40;
int n, m, g[M][M];
bool st[M];
// 检查行
bool check_row() {
for (int i = 0; i < m; i++) {
memset(st, 0, sizeof st);
for (int j = 0; j < m; j++) {
int val = g[i][j];
if (val < 1 || val > m) return false; // 超出范围
else if (st[val]) return false; // 重复
else st[val] = true; // 标记
}
}
return true;
}
// 检查列
bool check_col() {
for (int j = 0; j < m; j++) {
memset(st, 0, sizeof st);
for (int i = 0; i < m; i++) {
int val = g[i][j]; // 交换i和j即可
if (val < 1 || val > m) return false; // 超出范围
else if (st[val]) return false; // 重复
else st[val] = true; // 标记
}
}
return true;
}
// 检查方块
bool check_box() {
for (int x = 0; x < m; x += n)
for (int y = 0; y < m; y += n)
{
memset(st, 0, sizeof st);
for (int dx = 0; dx < n; dx++)
for (int dy = 0; dy < n; dy++) {
int i = x + dx, j = y + dy; // 计算真正坐标
int val = g[i][j];
if (val < 1 || val > m) return false; // 超出范围
else if (st[val]) return false; // 重复
else st[val] = true; // 标记
}
}
return true;
}
int main() {
int max_iter;
cin >> max_iter;
for (int iter = 1; iter <= max_iter; iter++) {
cin >> n;
m = n * n;
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
scanf("%d", &g[i][j]);
if (check_row() && check_col() && check_box())
printf("Case #%d: Yes\n", iter);
else
printf("Case #%d: No\n", iter);
}
return 0;
}
AcWing 703. 数独检查
思路:
依次检查行、列、方格即可。方格可通过二重循环偏移量dx和dy实现。
注意题目没说一定是9宫格,事实上是n^2宫格,因此需要注意读入过程。
方格循环里有很多坑:
- 步长变化是
x += n,而不是x++ memset()在第2层循环里,而不是像其它两个check在第1层循环里
代码实现:
#include <iostream>
#include <cstring>
using namespace std;
const int M = 40;
int n, m, g[M][M];
bool st[M];
// 检查行
bool check_row() {
for (int i = 0; i < m; i++) {
memset(st, 0, sizeof st);
for (int j = 0; j < m; j++) {
int val = g[i][j];
if (val < 1 || val > m) return false; // 超出范围
else if (st[val]) return false; // 重复
else st[val] = true; // 标记
}
}
return true;
}
// 检查列
bool check_col() {
for (int j = 0; j < m; j++) {
memset(st, 0, sizeof st);
for (int i = 0; i < m; i++) {
int val = g[i][j]; // 交换i和j即可
if (val < 1 || val > m) return false; // 超出范围
else if (st[val]) return false; // 重复
else st[val] = true; // 标记
}
}
return true;
}
// 检查方块
bool check_box() {
for (int x = 0; x < m; x += n)
for (int y = 0; y < m; y += n)
{
memset(st, 0, sizeof st);
for (int dx = 0; dx < n; dx++)
for (int dy = 0; dy < n; dy++) {
int i = x + dx, j = y + dy; // 计算真正坐标
int val = g[i][j];
if (val < 1 || val > m) return false; // 超出范围
else if (st[val]) return false; // 重复
else st[val] = true; // 标记
}
}
return true;
}
int main() {
int max_iter;
cin >> max_iter;
for (int iter = 1; iter <= max_iter; iter++) {
cin >> n;
m = n * n;
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
scanf("%d", &g[i][j]);
if (check_row() && check_col() && check_box())
printf("Case #%d: Yes\n", iter);
else
printf("Case #%d: No\n", iter);
}
return 0;
}
AcWing 1101. 献给阿尔吉侬的花束
思路:
迷宫问题,用BFS
注意入队条件:新坐标在边界内0 \leqslant i < m , \,\,0 \leqslant j < n,且不是墙壁g[i][j] != '#',且没有遍历过dist[i][j] == -1
代码实现:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 210;
typedef pair<int, int> PII;
char g[N][N];
int m, n, dist[N][N];
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
int bfs(PII start, PII end) {
memset(dist, -1, sizeof dist);
queue<PII> q;
// 放入起点
q.push(start);
dist[start.first][start.second] = 0;
while(!q.empty()) {
PII current = q.front();
q.pop();
for (int k = 0; k < 4; k++) {
// 当前位置及最短距离
int x = current.first, y = current.second, d = dist[x][y];
// 更新x和y
int x_new = x + dx[k], y_new = y + dy[k];
if (x_new >= 0 && x_new < m
&& y_new >= 0 && y_new < n
&& g[x_new][y_new] != '#' && dist[x_new][y_new] == -1) {
dist[x_new][y_new] = dist[x][y] + 1; // 更新距离
PII pos = {x_new, y_new};
if (pos == end) {
return dist[x_new][y_new]; // 找到终点,返回
}
q.push(pos);
}
}
}
return -1; // 找不到终点
}
int main() {
int t;
cin >> t;
while(t--) {
cin >> m >> n;
for (int i = 0; i < m; i++) cin >> g[i];
PII start, end;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (g[i][j] == 'S') start = {i, j};
else if (g[i][j] == 'E') end = {i, j};
int res = bfs(start, end);
if (res == -1) puts("oop!");
else printf("%d\n", res);
}
return 0;
}
AcWing 89. a^b
思路:
可参考算法基础课——快速幂
但那题中,b \geqslant 1,而本题b \geqslant 0。特别的,当b = 0, p = 1时,按“快速幂”的模板会得到结果1,而实际结果应该为0,因此需要在给res赋初值时,加上% p,即res = 1 % p
代码实现:
#include <iostream>
using namespace std;
typedef long long LL;
int main() {
int a, b, p;
cin >> a >> b >> p;
LL res = 1L % p; // 避免b为0,p为1时,结果为1
while(b) {
if (b & 1) res = (LL) a * res % p;
a = (LL) a * a % p;
b >>= 1;
}
cout << res % p << endl;
return 0;
}


666
666
666