开始最常见的最短路问题(之前不会最短路,不敢在信竞队里说出来)
最短路一般分为两种,分别是单源最短路和多源汇最短路。
源就是起点,汇就是终点,所以单源最短路就是一个点到其他点的最短距离;多源汇最短路就是多个起点到多个终点的最短距离。
往后还可以再细分,具体是这样的:
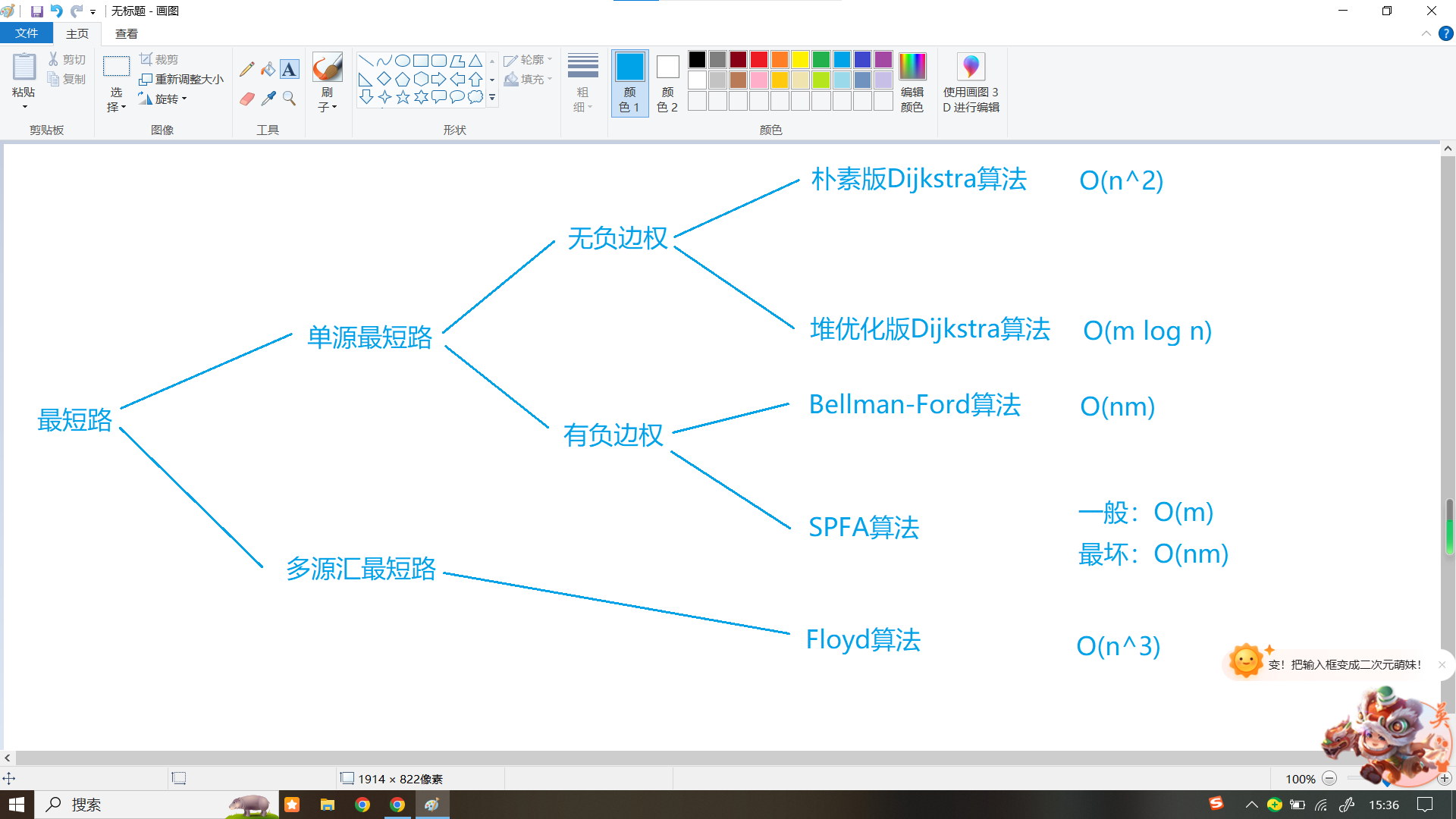
$n$代表点数,$m$代表边数。
这些算法按顺序说:
朴素版Dijkstra算法
第一步:先初始化距离:
用$dist$数组来存距离。
因为从1点开始,所以$dist[1] \leftarrow 0$
其他的都没遍历到,所以$dist[i] \leftarrow +\infty$
第二步:迭代
用集合$S$存已经确定最短距离的点。
循环$n$次,每一次执行以下操作
1. $t \leftarrow 不在S中的离i点最近的点$
2. 把$t$加到$S$里面去。
3. 用$t$更新其他点的距离,更新方式如下:
看一下原来从1号点到$i$号点和先从1号点到$t$号点,再从$t$号点到$i$号点哪个近,然后赋值为那个。
代码:
int dist[N];
bool s[N];
int dij(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 1; i <= n; i++){
int t = 0;
for (int j = 1; j <= n; j++){
if (!s[j] && (!t || dist[t] > dist[j]))
t = j;
}
s[t] = true;
for (int j = 1; j <= n; j++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if (dist[n] = 0x3f3f3f3f) return -1;
return dist[n];
}
堆优化版Dijkstra算法
他跟上面那个是差不多的,就是看看怎么做优化。
上面找最小距离的过程是$O(n)$的,怎么优化呢,可以用堆直接找到最小值。
代码:
int dist[N];
bool s[N];
int dij(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue< pair< int, int >, vector< pair< int, int > >, greater< pair< int, int > > > heap;
heap.push({0, 1});
while (heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (s[ver]) continue;
s[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if (dist[j] > dist[ver] + w[i]){
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
Bellman-Ford算法
第一步:迭代:
循环$n$次。
每次循环所有边。
然后再照着dijkstra的方式更新每一个点的距离。
第二步……没有第二步
在Bellman-Ford算法过后,会有一个式子叫做三角不等式,就是这样:
$$dist[i] \le dist[j] + 从j到i的那条边$$
众所周知,当图里有负环的时候,有可能没有最短路,但Bellman-Ford算法是可以判断负环的(虽然前面两位也行)。
这就是Bellman算法,一个非常暴力的算法。
代码:
由于Bellman-Ford算法处处不如SPFA,所以就弄这道题的代码吧。
int dist[N];
int last[N];
void bellman_ford(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 1; i <= k; i++){
memcpy(last, dist, sizeof dist);
for (int j = 1; j <= m; j++){
auto e = edges[j];
dist[e.b] = min(dist[e.b], last[e.a] + e.c);
}
}
}
请原谅我拿了yxc的代码。
SPFA算法
因为Bellman-Ford算法是一个非常傻的算法,所以SPFA就是Bellman-Ford算法的优化版。
众所周知,dist[b] = min(dist[a] + w, dist[b]),只有dist[a]变小,dist[b]才会变小,可以针对这一点来做优化,可以用宽搜做。
第一步:初始化一个队列$q$,存所有变小了的节点:
先把1号点存进去,然后以后再说。
第二步:迭代:
只要队列$q$不空,就重复执行以下步骤:
1. $t \leftarrow q.front(), q.pop()$
2. 更新$t$的所有出边,跟Dijkstra差不多。如果更新成功,就把它加入队列。
代码:
int dist[N];
bool s[N];
int spfa(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue< int > q;
q.push(1);
s[1] = true;
while (!q.empty()){
int t = q.front();
q.pop();
s[t] = false;
for (int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if (dist[j] > dist[t] + w[i]){
dist[j] = dist[t] + w[i];
if (!s[j]){
q.push(j);
s[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
好,spfa求最短路看完了,但还有spfa判负环,一般来说还是用spfa比较多,一般不用Bellman-Ford算法。
还是用容斥原理来判断。
开一个数组cnt,表示当前点到一号点的最小距离的边数。
每次$dist[j] = dist[t] + w[i]$的时候,$cnt[j] = cnt[t] + 1$就行了。
我们可以发现,如果$cnt[i] \ge n$就说明经过了$n+1$个点,而一共就$n$的点,就说明这里面肯定有环,还是负环,因为不是负环就不会有$cnt[i]$这个数字。
代码:
int dist[N], cnt[N];
bool s[N];
int spfa(){
queue< int > q;
for (int i = 1; i <= n; i++){
s[i] = true;
q.push(i);
}
while (!q.empty()){
int t = q.front();
q.pop();
s[t] = false;
for (int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if (dist[j] > dist[t] + w[i]){
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
if (!s[j]){
q.push(j);
s[j] = true;
}
}
}
}
return false;
}
Floyd算法
最后一个最短路算法,也是唯一一个多源最短路算法。
Floyd算法得用邻接矩阵存,主要是复杂度太高了,用邻接表存也没用。
这个就三层循环。
1. 用$k$循环一遍所有的点
2. 再用$i$循环一次所有的点
3. 最后用$j循环一次所有的点
每次让
$$d[i][j] = min(d[i][j], d[i][k] + d[k][j])$$
d[i][j]就是从i到j的最短距离,一开始就输入到这里面。
然后就没了暴力美学。
代码:
void Floyd(){
for (int k = 1; k <= n; k++){
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}

