树状数组(Binary-Indexed-Tree/Fenwick Tree)
Introduction
考虑如下的问题:给出一个数组,我们需要执行以下两种操作:
- 单点更新:修改数组中的某一个数字。
- 区间求和:求某一个区间内的数字之和。
对于问题一,我们通常可以在$O(1)$的时间内解决,对于问题二,我们通常可以在$O(n)$的时间内解决。如果我们使用前缀和解决问题二,我们可以在$O(1)$的时间内求解前缀和,但是我们修改数组元素时,则要重新计算一次前缀和数组$O(n)$。假设我们有$m$次查询,那么我们可以使用RMQ算法将总的时间复杂度降低到$O(mlogn)$,但是我们可以使用更容易编码(不超过十行)的树状数组在同样的时间复杂度下解决同样的问题。
Basic Idea
每一个整数可以由若干个整数组成,同样的,对于区间求和问题,我们可以将区间分解成若干个小区间进行求和。树状数组中为了方便后续计算,我们假设所有的数组下标从1开始。对于给定的数组$A[1,…,n]$,我们构造一个长度也为$n$的辅助数组$tree[1,..,n]$,特别的$tree[idx]$存储的是$sumRange(idx - 2^r + 1,idx)$共计$2^r$个数的和。这里的$r$代表的是$idx$的二进制表示中最低的非0位是第几位,如5(101)最低非0位是$r = 0$,所以$tree[5] = sumRange(5,5)$,同理6(110)的最低非0位是$r = 1$,所以$tree[6] = sumRange(6 - 2 + 1,6)$共两个数字的和。下面给出一个长度为16的树状数组辅助数组的值。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 0 | 2 | 1 | 1 | 3 | 0 | 4 | 2 | 5 | 2 | 2 | 3 | 1 | 0 | 2 |
| 前缀和 | 1 | 1 | 3 | 4 | 5 | 8 | 8 | 12 | 14 | 19 | 21 | 23 | 26 | 27 | 27 | 29 |
| Tree | 1 | 1 | 2 | 4 | 1 | 4 | 0 | 12 | 2 | 7 | 2 | 11 | 3 | 4 | 0 | 29 |
下面给出每个$tree[i]$对应的区间范围:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tree | 1 | [1,2] | 3 | [1,4] | 5 | [5,6] | 7 | [1,8] | 9 | [9,10] | 11 | [9,12] | 13 | [13,14] | 15 | [1,16] |
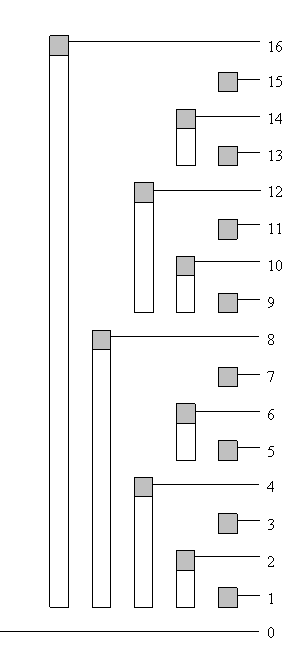
现在假设我们希望求前13个元素的和,我们发现13的二进制表示为1101,有趣的是我们发现$sumRange(1,13) = tree[1101] + tree[1100] + tree[1000]$。恰好每次把13二进制的的最后一个1去除。
Isolating the last bit
根据上述发现,我们如果能够快速的求出$n$的二进制表示中每个1的位置,我们就可以快速的求出其前缀和。对于任何一个非0的数它的二进制表示为a1b,b代表若干个0,a代表更高位的数字,我们知道计算机在表示负数的时候是使用补码将正数的二进制表示取反再加上1。考虑-n的二进制表示为$a^{-1}0b^{-1} + 1 = a^{-1}1b$。这里$a^{-1}$代表这部分二进制编码取反。
我们尝试$n\&(-n)$,我们可以得到
$a1b$
$\& a^{-1}1b$
$=(000)1(0000)$
所以对于每一个$idx$,它包含的区间大小恰好为$2^r = idx \&(-idx)$,$tree[idx] = sumRange(idx - 2 ^r +1,idx) $。
前缀和求解:
假设我们想求前$idx$个元素的前缀和,我们执行以下操作:
- 将$tree[idx]$的值加入到答案中
- 将$idx$的值减去$tree[idx]$包含的元素个数$idx \& -idx$
- 重复上述操作直至$idx <= 0$
int read(int idx)
{
int sum = 0;
while(idx > 0)
{
sum += tree[idx];
idx -= (idx & -idx);
}
return sum
}
下面我们给出$idx = 13$的求解示例
| Iteration | Idx | position of the last bit | idx &-idx | sum |
|---|---|---|---|---|
| 1 | 13 = 1101 | 0 | 1(2^0) | 3 |
| 2 | 12 = 1100 | 2 | 4(2^2) | 14 |
| 3 | 8 = 1000 | 3 | 8(2^3) | 26 |
| 4 | 0 = 0 | - | - | - |
[HTML_REMOVED]
时间复杂度$O(logn)$
单点更新:
我们在想修改数组中某一个元素的的值的时候,我们需要将$tree$数组中和包含待修改元素的值也做相应的修改。在求前缀和的过程中,我们不断的移除$idx$的最后一个比特位,有趣的是在单点更新的过程中,我们是不断的添加$idx$的最后一个比特位。我们执行以下操作。
- 修改$tree[idx]$ 的值
- 将$idx$值加上$idx \& -idx$
- 重复上述操作直至$idx > n$
// 注意这里的val指的是变化值delta而不是修改后的值
void update(int idx,int val)
{
while(idx <= n)
{
tree[idx] += val;
idx += (idx & -idx);
}
}
假设我们希望修改$idx = 5$的值,迭代过程如下:
| iteration | idx | position of the last bit | idx & -idx |
|---|---|---|---|
| 1 | 5=101 | 0 | 1(2^0) |
| 2 | 6=110 | 1 | 2(2^1) |
| 3 | 8=1000 | 3 | 8(2^3) |
| 4 | 16=10000 | 4 | 16(2^4) |
| 5 | 32=100000 | - | - |
[HTML_REMOVED]
时间复杂度$O(logn)$
单点查询
如果我们想获取数组元素$A[idx]$的值,我们通常由两种方法来做:
- 使用额外的空间来维护数组$A$,在每次单点更新的时候,同时更新数组$A$,这样我们可以在$O(1)$的时间内求解
- 使用两次区间查找,这是因为$A[idx] = sumRange(1,idx) - sumRange(1,idx - 1)$,这样我们可以在$O(logn)$的时间内求解。
假设我们希望求解一段区间内的和,这两个下标到根节点的路径,这两条路径肯定会在某个节点相遇,在那之后,他们会重叠,比如区间[6,7],$read[5] = tree[5] + tree[4]$,$read[7] = tree[7] + tree[4]$。$tree[4]$是他们共同的部分,其实没有必要计算。
现在假设我们希望查找$A[idx]$,我们令$x = idx,y = idx - 1$,在二进制表示中$y = a0b$,$b$代表连续的一段1,$x = a1b^-$,$b^-$代表连续的一段0。在$read(x)$第一次迭代后,我们会移除$x$最低位上的1,这个时候$x = a0b^-$,我们令$z = x = a0b^-$。这时候我们不断的将$y$低位的1抹除,我们可以得到$y = a0b^- = z$。这意味着从0到$x$和从0到$y$的路上相遇了。
int readSingle(int idx)
{
int sum = tree[idx];
int y = idx --;
if(idx > 0)
{
int idx = idx - (idx & -idx);
while(y!= idx)
{
sum -= tree[y];
y -= (y & - y);
}
}
return sum
}
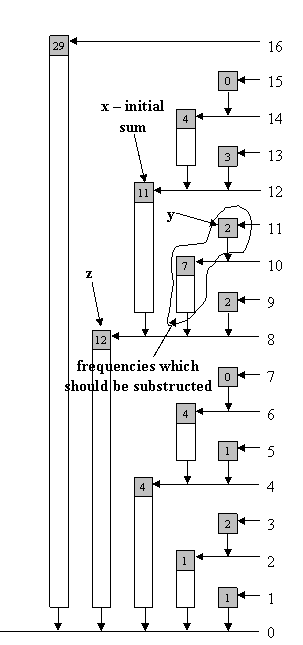
这个算法比调用两次$read$函数要快,并且当$idx$是奇数的时候,我们可以在第一次循环就跳出,使用$O(1)$的时间就可以得到答案。其实也就是$tree$中,奇数位置上存储的就是原数组中对应位置的元素。
区间求和
基于上述思想我们可以得到区间求和的算法:
inline int lowbit(x){return x & -x;}
int sumRange(int i,int j)
{
int res = 0;
i --;
while(i != j)
{
res = res + tree[j] - tree[i];
i -= lowbit(i);
j -= lowbit(j);
}
return res;
}
将数组元素缩放一个常数因子
void scale(int c){
for (int i = 1 ; i <= MaxIdx ; i++)
tree[i] = tree[i] / c;
}
求前缀和恰好等于target的index
如果数组中的元素有正有负我们只能遍历所有的$idx$,使用$read(idx)$函数求解,时间复杂度$O(nlogn)$。
如果数组中的元素只有非负数,那么我们可以利用二分的思想来求解,时间复杂度$O(lognlogn)$
二维树状数组
考虑如下的问题,在一个二维平面的第一象限中(坐标为正数),我们需要执行以下两种操作:
- 修改坐标$(x,y)$的值
- 求以坐标$(x,y)$为右上角,$(1,1)$为左下角的矩形区域总和。
与一维树状数组类似的,我们设计一个二维的树状数组来解决这个问题。
更新操作:
inline int lowbit(x){return x & -x;}
void update(int x,int y,int delta)
{
for(int i = x ; i <= A.size() ;i += lowbit(i))
{
for(int j = y;j <= A[0].size() ;j += lowbit(j))
{
A[i][j] += delta;
}
}
}
求和操作:
inline int lowbit(x){return x & -x;}
void read(int x,int y)
{
int sum = 0;
for(int i = x;i > 0 ; i -= lowbit(i))
{
for(int j = y;j > 0 ;j -= lowbit(j))
{
sum += A[i][j];
}
}
return sum;
}
区间修改、单点查询的树状数组
在这个问题中我们需要完成的任务是:
- 将一个区间内的数字增加同样一个值
- 求某一个位置的值。
在这里我们可以利用差分的思想,假设初始数组为$A$,我们首先构造一个关于$A$的差分数组$C$,其中$C[1] = A[1],C[i] = A[i] - A[i -1](i > 1)$。
那么我们想将区间$[L,R]$内的数字增加同样一个值,那么我们只需要修改差分数组中两个位置的元素$C[L] = C[L] + delta,C[R+1] = C[R + 1] - delta$。
如果我们想要求某一个位置的值$A[idx]$,那么$A[idx] = sumRange(C[1,idx])$。
基于上述思想,我们这里的树状数组$tree$是关于差分数组$C$的。
inline int lowbit(int x) {return x & -x;}
void init(int[] A)
{
int n = A.size();
for(int i = 1;i < n;i ++)
{
C[i] = A[i] - A[i - 1];
update_dot(i,C[i]);
}
}
void update_dot(int idx,int val)
{
while(idx <= n)
{
tree[idx] += val;
idx += (idx & -idx);
}
}
void update(int L,int R,int delta)
{
update_dot(L,delta);
update_dot(R,-delta);
}
void read(int idx)
{
int res = 0;
while(idx > 0)
{
res += tree[idx];
idx -= lowbit(idx);
}
return res;
}
区间修改、区间查询树状数组
在这个任务中,我们需要解决以下问题:
- 将一个区间内的值添加同样的数值
- 查询一个区间的和
上述问题可以使用线段树解决,但是稍微改进我们的树状数组也是可以完成上述任务的。同样的我们使用上一节中定义的差分数组$C$。我们知道,如果我们想求解一个$S = A[1:n]$前缀和的话,有:
S = A[1] + A[2] + ... + A[n]
= C[1] + (C[1] + C[2]) +...+(C[1]+C[2]+...+C[n])
= n * C[1] +(n - 1)*C[2] +...+1*C[n]
= (n + 1)*(C[1] + C[2]+...+C[n]) - (1*C[1]+2*C[2]+...+n*C[n])
因此我们可以使用另一个辅助数组$D$来维持$D[i] = i*C[i]$的值,整体代码和上述代码相似。下面给出模板题(线段树可做)。这里tree1和tree2分别代表的是辅助数组$C$和辅助数组$D$的树状数组。
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const static int N = 100010;
typedef long long ll;
int n,m;
ll A[N],tree1[N],tree2[N];
inline int lowbit(int x) {return x & -x;}
void update_dot(int idx,ll delta)
{
for(int i = idx ; i <= n ; i += lowbit(i))
{
tree1[i] += delta;
tree2[i] += idx * delta;
}
}
void updateRange(int l,int r,ll delta)
{
update_dot(l,delta);
update_dot(r + 1,-delta);
}
ll ask(int idx)
{
ll res = 0;
for(int i = idx ;i > 0;i -=lowbit(i))
res += (idx + 1) * tree1[i] - tree2[i];
return res;
}
ll rangeQuery(int l,int r)
{
return ask(r) - ask(l - 1);
}
int main()
{
scanf("%d %d",&n,&m);
for(int i = 1; i <= n ; i ++)
{
scanf("%lld",&A[i]);
update_dot(i,A[i] - A[i - 1]);
}
for(int i = 1; i <= m ; i ++)
{
char ch;
cin >> ch;
if(ch == 'Q')
{
int start,end;
ll delta;
scanf("%d %d",&start,&end);
printf("%lld\n",rangeQuery(start,end));
}else
{
int start,end;
ll delta;
scanf("%d %d %lld",&start,&end,&delta);
updateRange(start,end,delta);
}
}
return 0;
}
线段树解法请看 线段树入门笔记


写的真好,今晚就睡这里了
做leetcode,知道还有这种数据结构,找了将近一天的资料, 直到博主那个图我猜恍然大悟,感谢
每一个整数可以由若干个整数组成,同样的,对于区间求和问题,我们可以将区间分解成若干个小区间进行求和。树状数组中为了方便后续计算,我们假设所有的数组下标从1开始。对于给定的数组A[1,…,n]A[1,…,n],我们构造一个长度也为nn的辅助数组tree[1,..,n]tree[1,..,n],特别的tree[idx]tree[idx]存储的是sumRange(idx−2r+1,idx)sumRange(idx−2r+1,idx)共计2r2r个数的和。这里的rr代表的是idxidx的二进制表示中最低的非0位是第几位,如5(101)最低非0位是r=0r=0,所以tree[5]=sumRange(5,5)tree[5]=sumRange(5,5),同理6(110)的最低非0位是r=1r=1,所以tree[6]=sumRange(6−2+1,6)tree[6]=sumRange(6−2+1,6)共两个数字的和。下面给出一个长度为16的树状数组辅助数组的值。
这段说的太好了 ,清晰。