栈

栈是 OI 中常用的一种线性数据结构，请注意，本文主要讲的是栈这种数据结构，而非程序运行时的系统栈/栈空间
栈的修改是按照后进先出的原则进行的，因此栈通常被称为是后进先出（last in first out）表，简称 LIFO 表。

栈是一个简单的数据结构,只要记住他是先进后出即可,在STL提供了一个方法 std::stack

#include <stack>
// stack 构造 ：
1. stack<Typename T> s;
2. stack<Typename T, Container> s;
/* stack 的 Container 需要满足有如下接口 ：
 * back()
 * push_back()
 * pop_back()
 * 标准容器 std::vector / deque / list 满足这些要求
 * 如使用 1 方式构造，默认容器使用 deque
 */

std::stack 支持赋值运算符 =

元素访问：

s.top() 返回栈顶

容量：

s.empty() 返回是否为空

s.size() 返回元素数量

修改：

s.push() 插入传入的参数到栈顶

s.pop() 弹出栈顶

其他运算符：

== 、 != 、 < 、 <= 、 > 、 >= 可以按照字典序比较两个 stack 的值

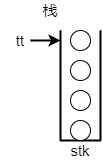
同时,我们也可以用数组来模拟栈,模拟栈需要一些准备.

1. 创建一个stk[]数组,用来存储
2. 创建一个tt,表示栈顶

代码实现

// tt表示栈顶
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0) {}

以上即是栈的简单实现了.
练练? ACwing 828.模拟栈

单调栈

顾名思义，单调栈即满足单调性的栈结构

单调栈属实太抽象了,我不会但还是要冲tm的
单调栈虽然很抽象,但应用的题目是很少的(废话)
看题 ACwing 830.单调栈

这道题我看到第一眼,好家伙,暴力冲
But,时间复杂度太高,给我干趴下了.正解是用单调栈来做
解题思路:

给定我们一个序列,我们需要找到第i个数左边第一个比它小的数.
我们可以把i左边所以数存进栈中,每次从栈顶开始找,直至找到第一个比第i小的数.暴力大法好!
找到第一个比i小的数,通过这个我们可以挖掘出一些性质:
假设我们有一个数列:a1,a2,a3,a4,…ai
我们要找ai左边第一个小于ai的数,如果a2 > a4,那么a2是不是就永远不会被当做答案被输出
因为a4比a2小,而且在a2的后面,离ai更近
那么a4后面所有数的左边第一个最小的数再怎么说也不可能会是a2,那么a2是不是可以删掉?
通过这一性质,我们可以在每个数入栈时,进行比较,如果ax < ay,并且ax在ay左边,那么ay就可以删掉
只要满足这样的关系,我们就可以把前面的数删除,那么剩下的数就是单调的了.

实现:我们用tt来维护栈,每次读入一个数x,如果栈是不空的,并且stk[tt] >= x,那么tt- -
然后判断,如果栈为空,则说明不存在,输出-1,不为空,则输出栈顶元素
代码实现:

#include<iostream>
using namespace std;
const int N = 100010;
int n, stk[N], tt;
int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++)
    {
        int x;
        cin >> x;
        while(tt && stk[tt] >= x) tt --;
        if(tt)cout << stk[tt] << ' ';
        else cout << "-1 ";
        //不要忘记把x入栈
        stk[ ++ tt] = x;
    }
    return 0;
}

以上就是单调栈了,顺便附上模板

常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

队列

队列（queue）是一种具有「先进入队列的元素一定先出队列」性质的表。由于该性质，队列通常也被称为先进先出（first in first out）表，简称 FIFO 表。

C++ STL 中实现了 队列 std::queue 和 优先队列 std::priority_queue 两个类，定义于头文件 <queue> 中。
同样,我们通常用数组来模拟队列

普通队列

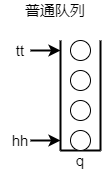
1. 创建一个q[]数组,用来存储
2. 创建一个hh,表示队头
3. 创建一个tt,表示表示队尾

代码实现

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt) {}

以上就是普通队列的实现方式了.
练练 ACwing 829.模拟队列

循环队列

使用数组模拟队列会导致一个问题：随着时间的推移，整个队列会向数组的尾部移动，一旦到达数组的最末端，即使数组的前端还有空闲位置，再进行入队操作也会导致溢出（这种数组里实际有空闲位置而发生了上溢的现象被称为“假溢出”）。
解决假溢出的办法是采用循环的方式来组织存放队列元素的数组，即将数组下标为 0的位置看做是最后一个位置的后继。（数组下标为 x 的元素，它的后继为 (x + 1) % size ）。这样就形成了循环队列。

代码实现

// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh != tt) {}

双端队列

双端队列是指一个可以在队首/队尾插入或删除元素的队列。相当于是栈与队列功能的结合。具体地，双端队列支持的操作有 4 个：

• 在队首插入一个元素
• 在队尾插入一个元素
• 在队首删除一个元素
• 在队尾删除一个元素

实现方式与数组模拟普通队列相同

单调队列

单调队列的重点分为 “单调” 和 “队列”
“单调” 指的是元素的的 “规律”——递增（或递减）
“队列” 指的是元素只能从队头和队尾进行操作

单调队列也好抽象,我还是不会
来看看单调队列的典型应用 ACwing 154.滑动窗口
解题思路:

首先我们用队列来维护一个窗口,每次在队尾插入一个数,再从队头弹出一个数,每次保证队列中只有当前窗口的所有元素.
求队列的最大值和最小值可以遍历一下队列的所有元素,暴力大法好!
But,时间复杂度太高,我们该考虑如何优化
我们来看看样例(以最小值为例)



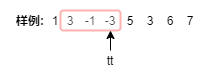
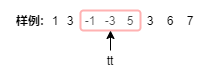
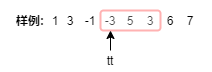
发现了嘛,我们每次输出的最小值都是-3.
通过观察我们可得,要是前面的数比后面的数大,那么它便不会被当做最小值输出,那么它是不是就可以删掉?
假设有一个数列:a1,a2,a3,a4,…ai
通过上面的分析可得,如果ax < ay,并且ax在ay的前面,那么ax便不会被当做最小值输出,便可以删掉ax
因为ax > ay,并且ax在ay前,那么ax便会先出队,也就是说ax在的时候ay也在,那么最小值就不可能是ax,ax就可以删除,最大值同理可得

实现:

1. hh,tt判断队头是否滑出窗口,hh表示队列的头,tt表示队列的尾.
2. 当队列不为空时,且当队列队尾元素>=当前元素(a[i])时,那么删除队尾元素
3. 加入新元素
4. 输出
   代码实现:

#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n, k, q[N], a[N];//q[N]存的是数组下标
int main()
{
    int tt = -1, hh=0;//hh队列头 tt队列尾
    scanf("%d%d",&n,&k);
    for(int i = 0; i <n; i ++) scanf("%d",&a[i]);
    for(int i = 0; i < n; i ++)
    {
        //维持滑动窗口的大小
        if(hh <= tt && k < i - q[hh] + 1) hh ++;
        //构造单调递增队列
        //当队列不为空,且当队尾元素>=当前元素(a[i]),那么删去队尾元素
        while(hh <= tt && a[q[tt]] >= a[i]) tt --;
        //加入新元素
        q[ ++ tt] = i;
        if(i + 1 >= k) printf("%d ", a[q[hh]]);
    }
    puts("");
    //输出最大值,反着来就行
    hh = 0,tt = -1;
    for(int i = 0; i < n; i ++)
    {
        if(hh <= tt && k < i - q[hh] + 1) hh ++;
        while(hh <= tt && a[q[tt]] <= a[i]) tt --;
        q[ ++ tt] = i;
        if(i + 1 >= k ) printf("%d ", a[q[hh]]);
    }
    return 0;
}

以上就是单调队列,附上模板

常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

参考资料

算法基础课
oi wiki