终于学到图论与搜索了，一天天都快愁死我了（做啥题啥不会）

这次的知识点有两个:

1. DFS
2. BFS

DFS:

DFS（Depth First Search）就是深度优先搜索。

他是一个固执的小孩，对于一个图，他总会一条路走到黑，直到没路了，他也不会直接回去，而是一边往回走，一边看看有没有其他路，有就继续一条道走到黑。
就比如有这么一张图：

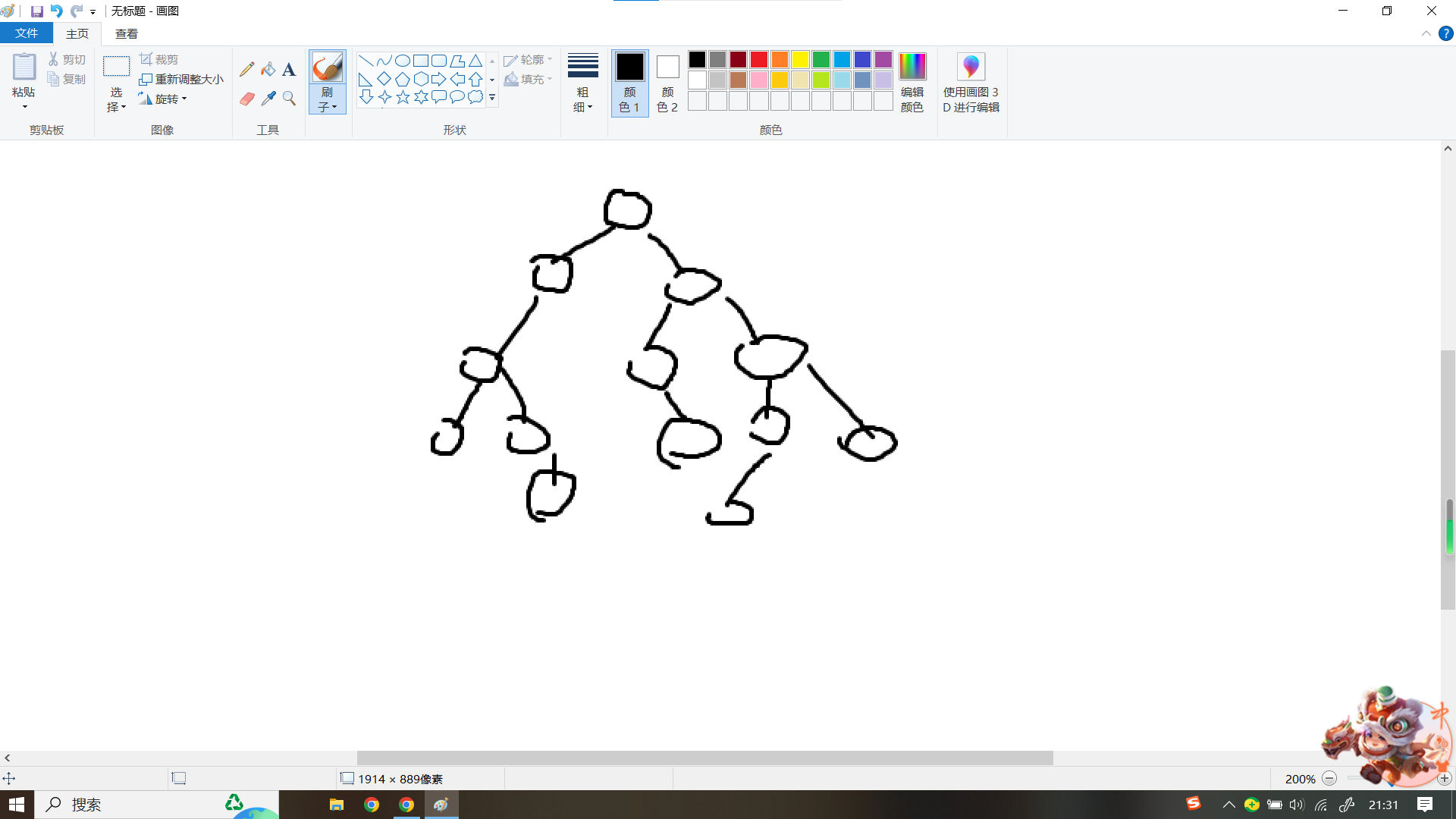
他的遍历顺序就是这样的（蓝色箭头）：

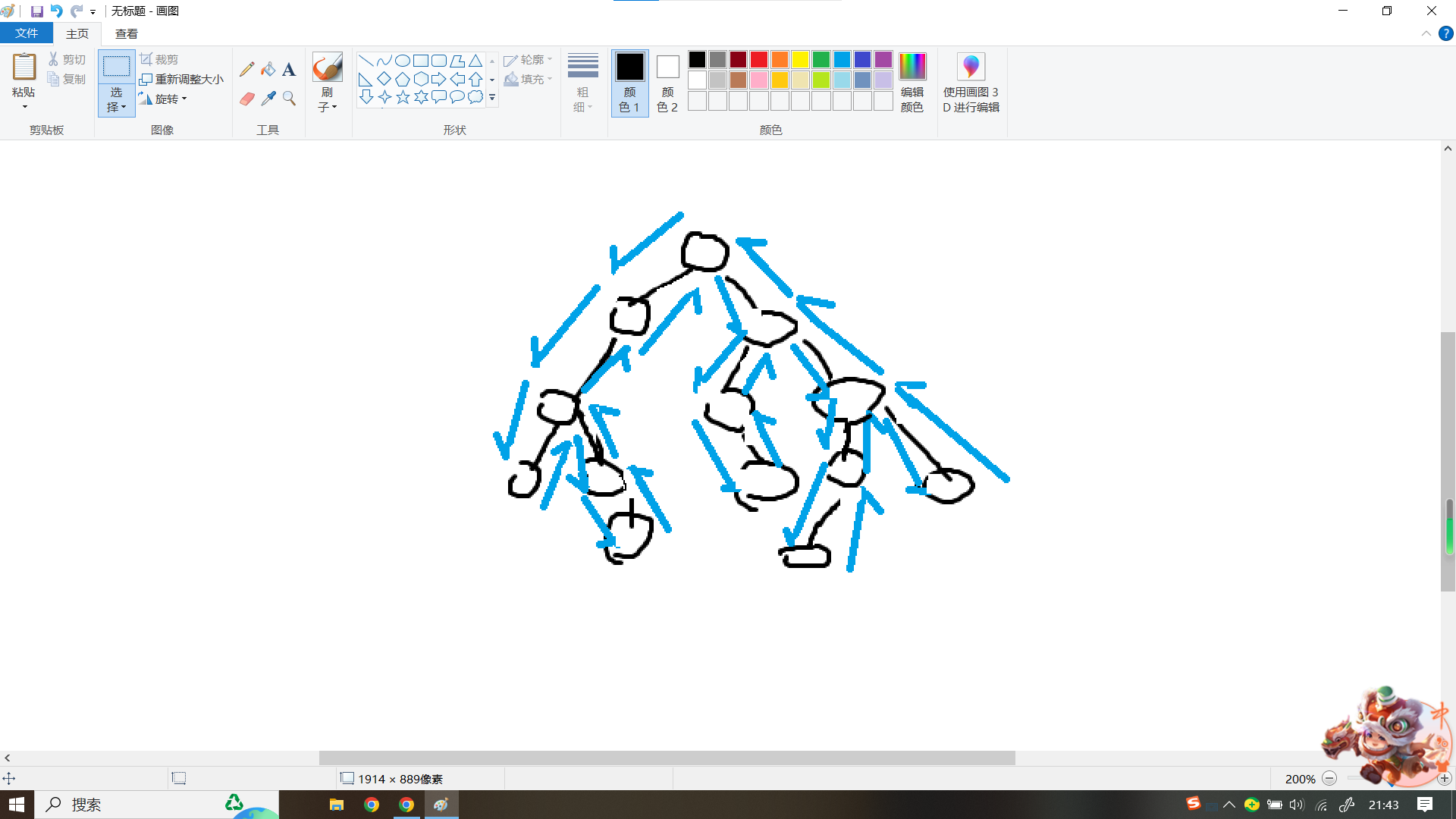
DFS是用栈实现的，空间复杂度是$O(h)$（h是深度）

DFS有两大概念，一个是回溯，一个是剪枝。
可以通过一道题理解回溯(全排列)、一道题理解剪枝(n皇后)。

全排列（回溯）：

思路：

DFS俗称爆搜，也就是把所有答案都搜一遍，而“全”排列就是所有答案。
DFS讲究的是顺序。
假设一开始有三个空位，然后每个空位都从1开始填，如果这个数前面填过了就不能填了，具体是这样的：

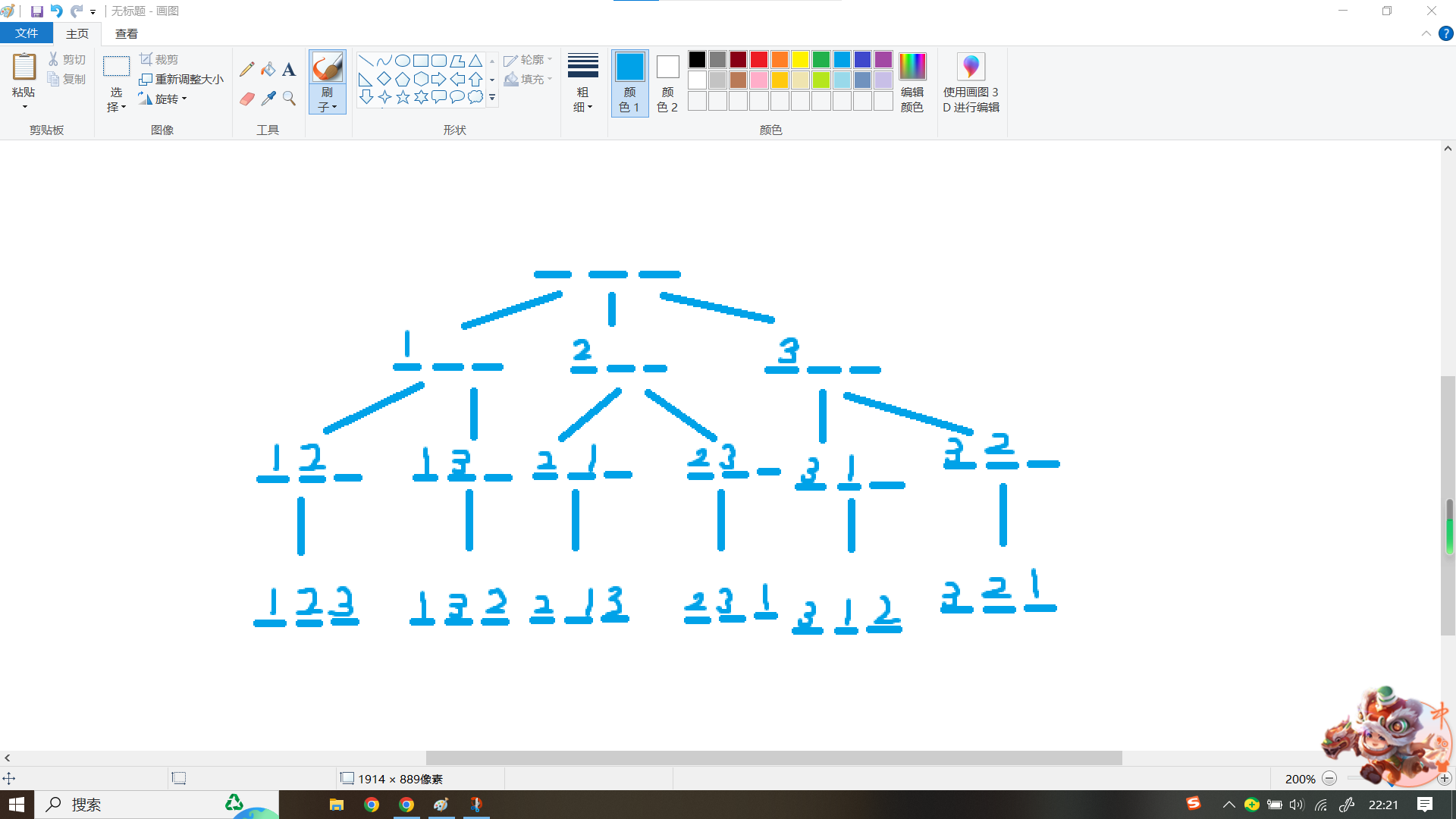
先看如果第一位填1会怎么样，然后往下看如果第二位填1的话就重复了，于是只能再填2，再往下发现第三位只能填3了不能填别的，于是填上3后往回走，这个往回走的过程就叫回溯，往回走到第二层，发现除了2以外第二位还能填3，于是就往下分支。第一位填1的话就结束了，然后再是填2，填3……

回溯有一个关键点就是要恢复现场，不能人家把那个数都撤了，你还记录着它存在过。

代码：

int n/*全排列数的个数*/, daan[10]/*答案数组*/;
bool b[10]/*判断这个数是否被用过*/;

void dfs(int idx/*表示现在填到第几个数了*/){
    if (idx == n){ // 搜出一个答案
        for (int i = 0; i < n; i++) printf("%d%c", daan[i], i == n - 1 ? '\n' : ' ');
        return ;
    }
    for (int i = 1; i <= n; i++){ // 从1开始遍历
        if (!b[i]){ // 如果这个数之前没被用过就用
            daan[idx] = i; // 将这个数设成答案的一部分
            b[i] = true; // 将这个数标记为用过
            dfs(idx + 1); // 再次遍历下一个位置
            b[i] = false; // 恢复现场
            // daan数组不用改，因为将来会被覆盖掉
        }
    }
}

n皇后

思路：

第一种方法：

可以用上一个题的思路。n个空位，第n个空位代表第n行的皇后在第几列，然后用三个数组记录，竖线，斜线，反斜线的位置上能不能放皇后，然后其他的一样了就。再就是斜线和反斜线用数组怎么表示，斜线是$dg_x+y$，x、y分别是横、竖线，反斜线是$udg_x-y+n$，y总的解释没看懂，反正记住就行。

第二种方法：

可以挨个遍历每一个格子，每次都有放皇后和不放两种选项，如果要放就要先看看能不能放，如果能放就遍历放和不放两种，反之就遍历不放这一种。

要是不能放的话，就说明假设放了之后的所有假设全部破碎，就不用再遍历了，这就叫剪枝。

代码：

第一种方法：

char daan[100][100];
int n;
bool col[100]/*竖线*/, dg[100]/*斜线*/, udg[100]/*反斜线*/;

void dfs(int idx){
    if (idx == n){
        for (int i = 0; i < n; i++) cout << daan[i] << '\n';
        printf("\n");
        return ;
    }
    for (int i = 0; i < n; i++){
        if (!col[i] && !dg[i + idx] && !udg[n - idx + i]){
            daan[idx][i] = 'Q';
            col[i] = dg[i + idx] = udg[n - idx + i] = true;
            dfs(idx + 1);
            daan[idx][i] = '.';
            col[i] = dg[i + idx] = udg[n - idx + i] = false;
        }
    }
    // 其他的跟全排列都差不多。
}

第二种方法：

#include<bits/stdc++.h>

using namespace std;

char daan[100][100];
int n;
bool row[100]/*横线*/, col[100], dg[100], udg[100]; // 其余与上个一样

void dfs(int x, int y, int s){ // x表示遍历到第几横行，y表示遍历到第几竖行，s表示放了几个皇后。
    if (y == n){
        y = 0;
        x++;
    }
    if (x == n){
        if (s == n){
            for (int i = 0; i < n; i++) cout << daan[i] << '\n';
            printf("\n");
        }
        return ;
    }
    // 以上是移动坐标的偷懒代码
    dfs(x, y + 1, s); // 直接dfs不放会怎么样
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]){ // 先判断能不能放
        daan[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        daan[x][y] = '.';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        // 放皇后的操作以及回溯
    }
}
int main(){
    scanf("%d", &n);
    for (int i = 0; i < n; i++){
        for (int j = 0; j < n; j++){
            daan[i][j] = '.';
        }
    }
    dfs(0, 0, 0);
    return 0;
}

第二种方法的效率要比第一种的要低一些。

至此，dfs结束

BFS

BFS（Breadth First Search）就是宽度优先搜索，也称广度优先搜索（我一般念广度，但y总念宽度）。

他是一个好奇心很强而且家里很有钱的小孩，对于一个图，他遇到岔路就会派个人往那个岔路走一走，他喜欢一次走完所有路。
就比如有这么一张图：

他的遍历顺序就是这样的（绿色）：

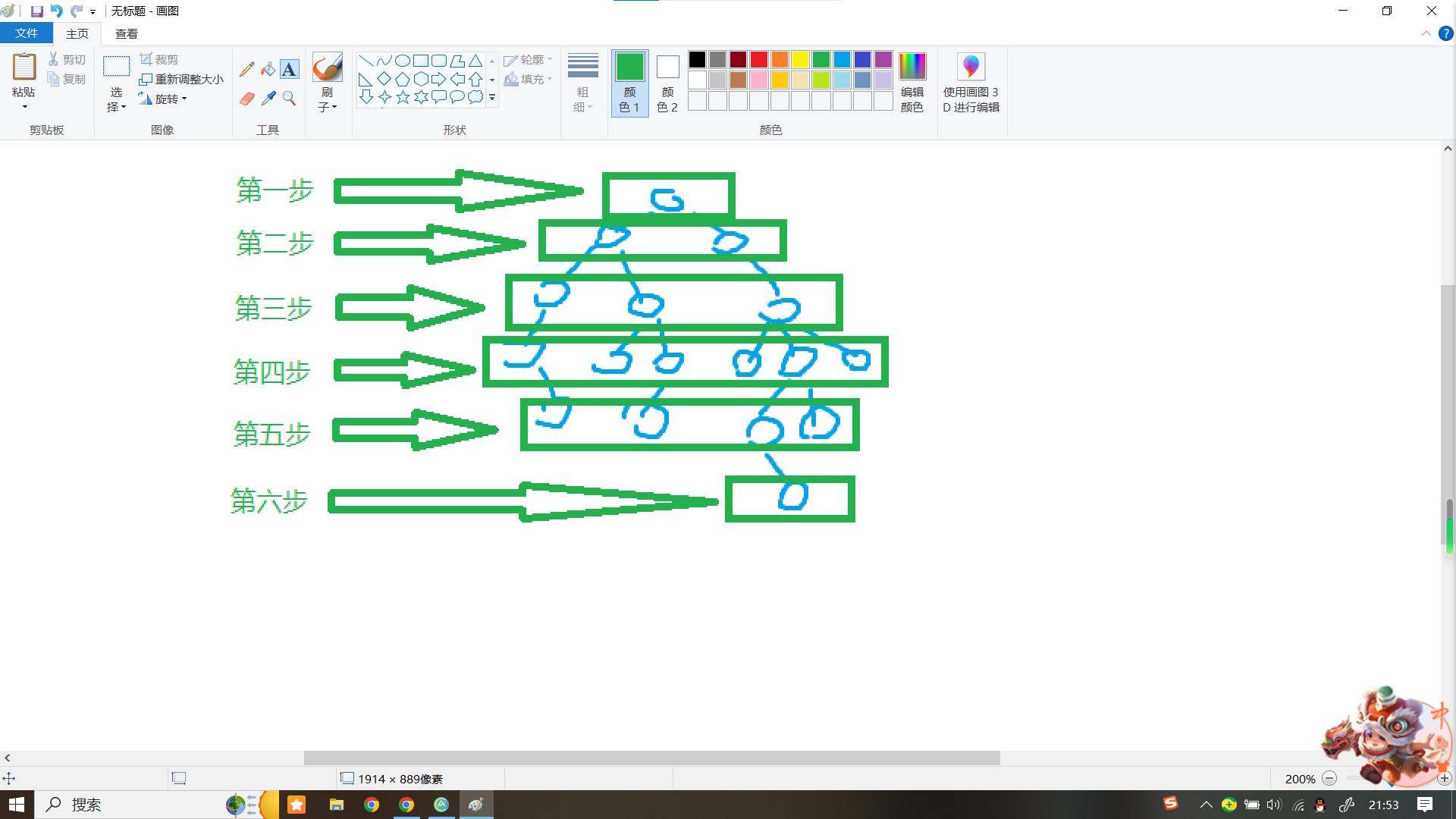
BFS是用队列实现的，空间复杂度是$O(2^h)$（h是深度），不过他有最短性，可以做部分最短路的题目。

那他为什么会有最短性呢？因为它是一圈一圈搜索的，先搜到的肯定是最短的，前提是权值要为1。

那么来看一下这道题

思路：

这道题用BFS来解，先看看样例，他最快的明显是下、下、右、右、右、右、下、下，那么用BFS怎么遍历出来呢？看下图：

抄的y总的图，不要在意，数字代表第几步可以走到哪。发现到终点了最快的是8，就代表最少8步可以到达终点。

BFS的框架就是先把初始状态放进队列，然后只要队列不空，就把队头移出去，然后扩展队头。
可能是我的理解能力有问题，反正上面那段话我看不懂，于是直接看代码。

代码：

const int N = 110;
int n, m;
int g[N][N], d[N][N];

int bfs()
{
    queue<PII> q;

    memset(d, -1, sizeof d);
    d[0][0] = 0;
    q.push({0, 0});

    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        for (int i = 0; i < 4; i ++ )
        {
            int x = t.first + dx[i], y = t.second + dy[i];

            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
            {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x, y});
            }
        }
    }

    return d[n - 1][m - 1];
}

STL版：

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N = 105;
int n, m, d[N][N];
bool g[N][N];
queue<pair<int, int> > B;

int bfs(){
    B.push({1, 1});
    memset(d, -1, sizeof d);
    d[1][1] = 0;
    int fang[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
    while (!B.empty()){
        auto F = B.front();
        B.pop();
        for (int i = 0; i < 4; i++){
            int x = F.first + fang[i][0], y = F.second + fang[i][1];
            if (x >= 1 && x <= n && y >= 1 && y <= m && !g[x][y] && d[x][y] == -1){
                d[x][y] = d[F.first][F.second] + 1;
                B.push({x, y});
            }
        }
    }
    return d[n][m];
}
signed main(){
    scanf("%lld%lld", &n, &m);
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= m; j++){
            scanf("%lld", &g[i][j]);
        }
    }
    printf("%lld", bfs());
    return 0;
}