在有序序列中查找一个元素，使用二分法，时间复杂度是 O(logn)。

如果数据是已链表的形式的存储的，链表不能通过索引获取元素，二分法就不能用了。不过可以使用跳表进行快速查找。跳表是有序链表与二分法的结合。

二分法查找依赖于数组的有序与随机访问，只能在数组中实现。

当数据存储在链表中的时候，只需要对链表进行改造，就可以实现类似于二分的查找算法，这种改造后的链表，叫做跳表(Skip List)。

假设有一个有序链表，我们需要查找某个节点，需要逐个的遍历链表。时间复杂度是 O(n)。

例如下面的链表中查找 15 这个节点，需要从链表头顺着指针逐个比较各个节点。需要从 0 -> 3 -> 7 -> 10 -> 12 -> 15，经过了 6 个节点。
我们可以对链表进行改造，想办法用空间换时间，就能实现有序链表的快速检索。

想想我们有一本很厚的书，现在想要看第三章的内容，是如何进行的？

先在目录出找到第三章所在页码：50，直接翻到书中的 50 页，就找到了第三章的内容。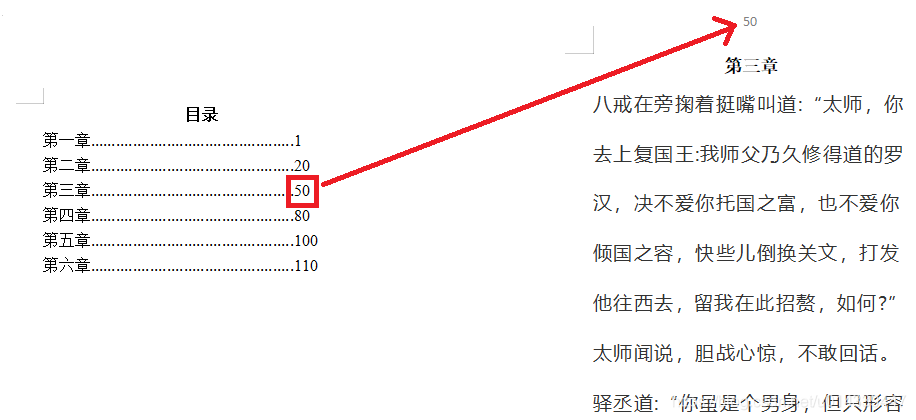
书的内容是按照第一章，第二章，第三章··· 排列的，可以看做一个有序链表。

有了目录的存在，在查找某一章的时候，先在目录中找到该章所在的页码，然后根据页码就能快速找到对应的章。相当于实现了链表的快速查找。

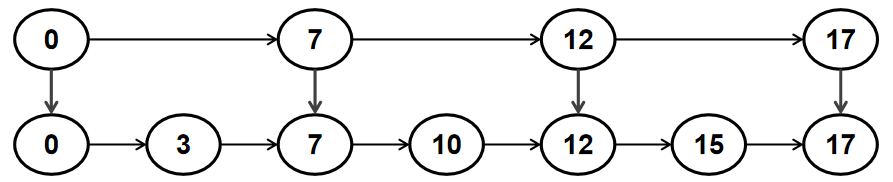
对链表进行改造，把一些节点从有序链表中提取出来，构成索引，相当于给链表添加一个目录。这样链表就变成了跳表。如下图：
在改造成跳表的链表中查找 15，只需要从 0 -> 7 -> 12 -> 15，经过了 4 个节点。检索的时间复杂度近似于 O(n/2)，这样检索的次数就减少了一半。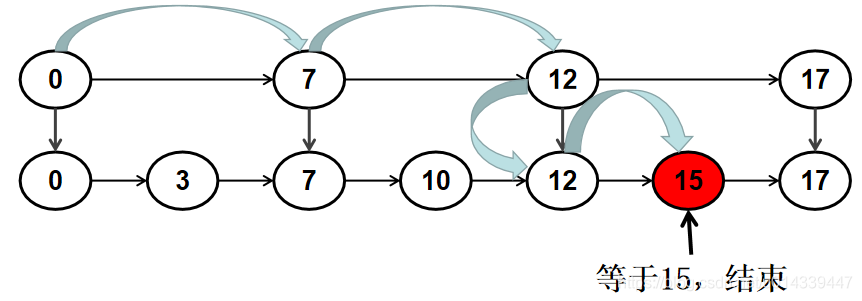
在改造成跳表的链表中查找 15，只需要从 0 -> 7 -> 12 -> 15，经过了 4 个节点。检索的时间复杂度近似于 O(n/2)，这样检索的次数就减少了一半。

当节点数量很多时，检索速度依旧很慢。我们可以提取一半数量的索引节点，构造索引的索引，形成多级索引，优化检索速度。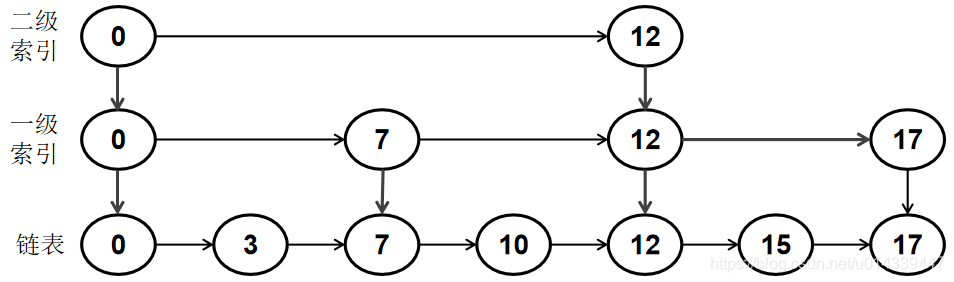
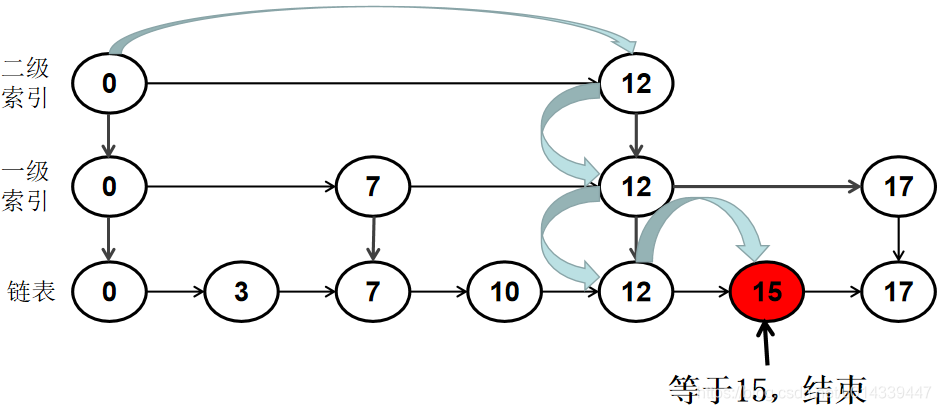
下图为在构造了二级索引后，检索 15 的过程。

• 有了2级索引之后，15先和二级索引比较，确定大体范围
• 然后再和一级索引比较，缩小检索范围

• 最后再回到原链表进行检索
  多级索引构造的思路如下：

• 假设原来的节点数量是 n。

• 提取一半节点构成一级索引，一级索引节点的数量为 n/2。
• 提取一级索引一半的节点构成二级索引，二级索引节点的数量为 n/4。
• 提取二级索引一半的节点构成三级索引，三级索引节点的数量为 n/8。
• 直到顶级索引的节点数量为 2。

索引的总层数为 logn。检索每级索引的时间复杂度是常数，所以检索的总时间复杂度为 O(logn)。

跳表的插入

跳表的插入分为两步：1. 在原始链表中插入数据。2. 调整索引。

例如在 0 -> 3 -> 7 -> 10 -> 12 -> 15 ->17 中插入 8 。

在原始链表中插入节点：

在原始链表中插入数据首先需要确定要插入的位置，利用跳表查找节点的方法，找到待插入位置。然后用普通链表的插入方法，将 8 插入到链表。

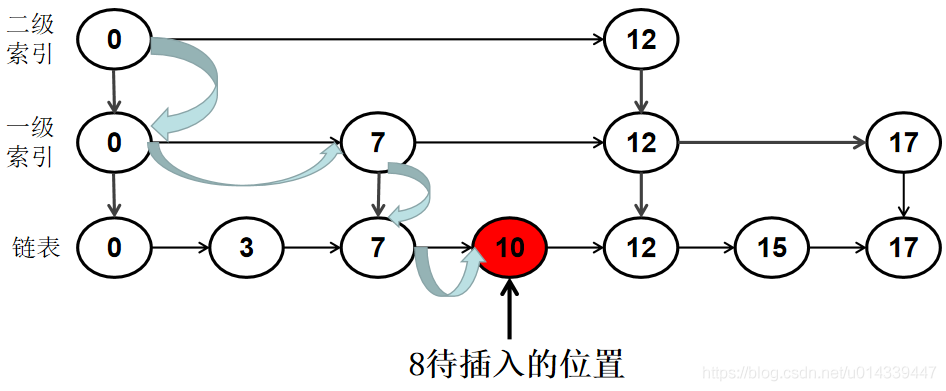
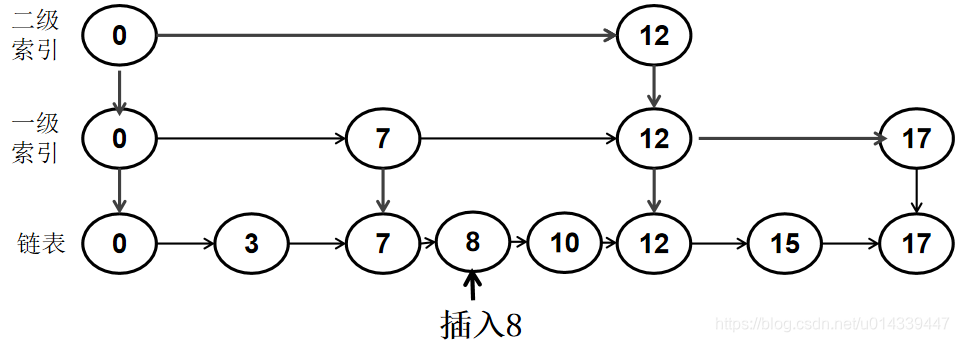
调整索引：

在不断插入新节点的过程中，链表的长度不断增加，索引需要进行调整。

索引最理想的情况是：每级索引节点的个数是下一层节点个数的一半。如果想要保持这种特向，可以在插入新节点后，删除原来索引，重新生成一个新的索引。重新生成索引的时间复杂度是 O(n)，代价太大。

每级索引节点的个数是下一层节点个数的一半。根据这个性质，跳表的发明者给出了一个很巧妙的方法：使用随机法，每插入一个新的节点，这个节点有 50% 的概率上升得到上级索引。这样时间复杂度就是 O(1) 了。

假设插入 8 后第一次上升成功，那么把结点 8 作为索引结点，插入到第一级索引的对应位置，并且向下指向链表的节点 8：

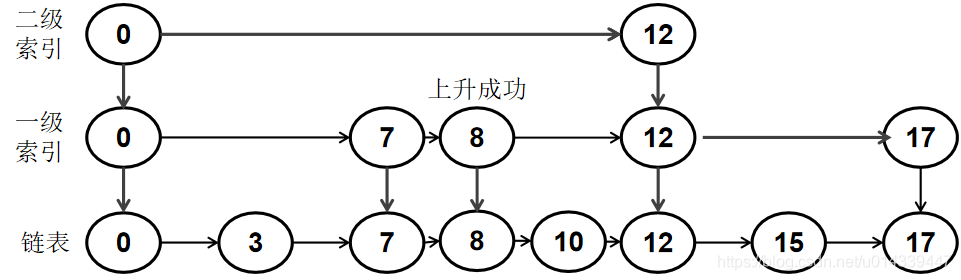
8 上升成功后，再次进行随机，决定是否再次上升。

新插入的节点不能无限上升。一般情况下，如果上升到最顶级索引后，如果随机化后仍要继续上升，就新增加一级索引，然后停止上升。

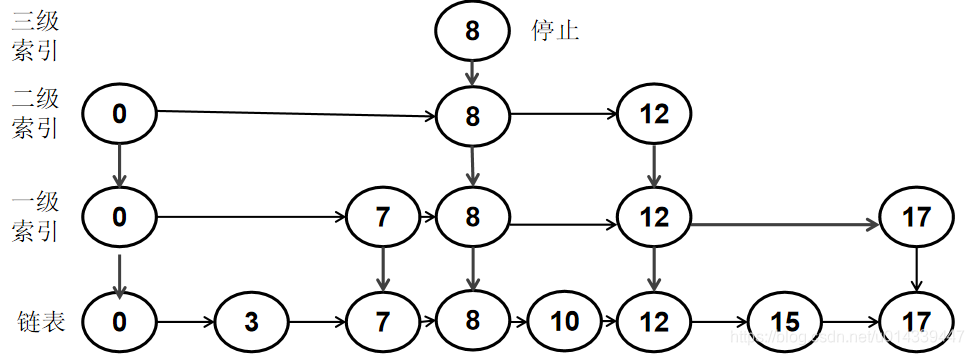
跳表的删除

在跳表中检索该节点，如果在索引中找到了要删除的节点，就从找到位置开始，一路向下删除。

例如删除节点 8。首先在索引中找到了节点 8，然后从该位置一路向下删除。



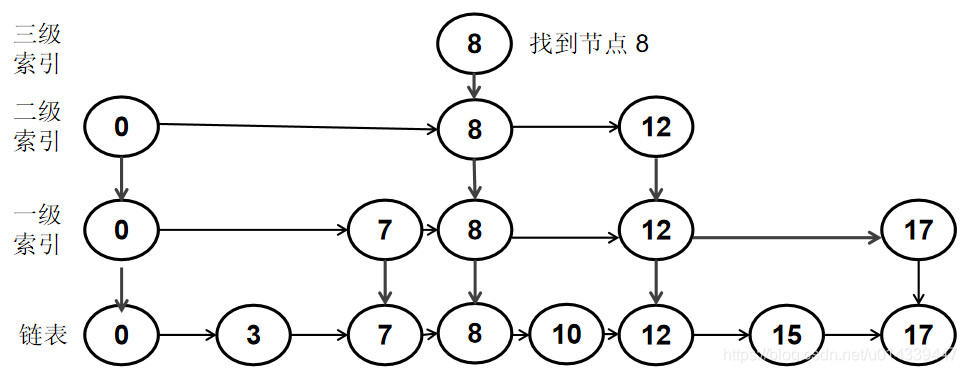
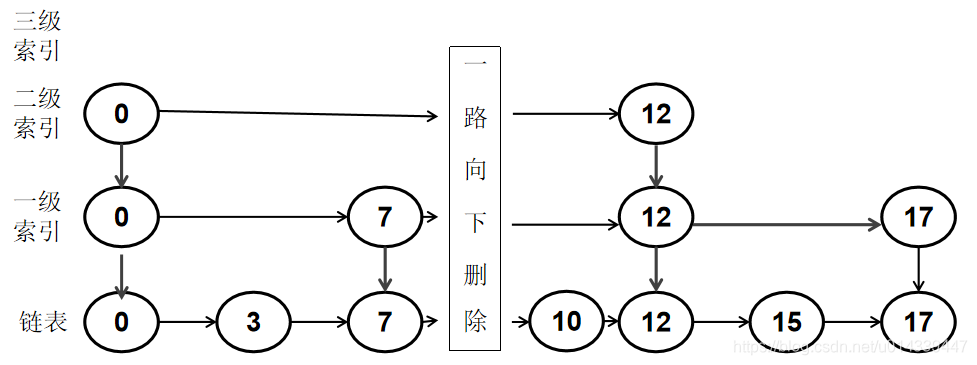
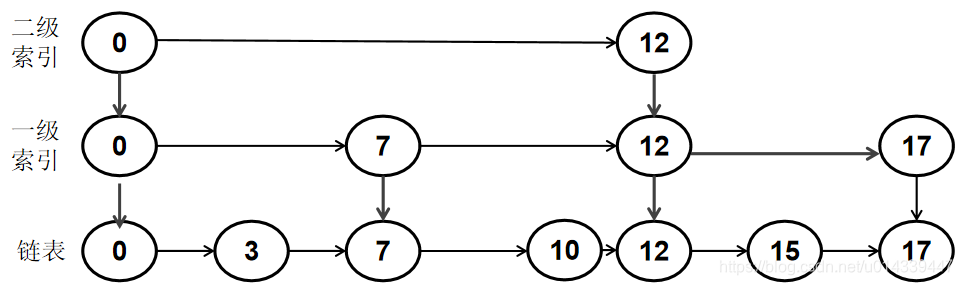
如果在索引中不存在要删除的节点，直接再链表中删除即可。

例如删除节点 10。


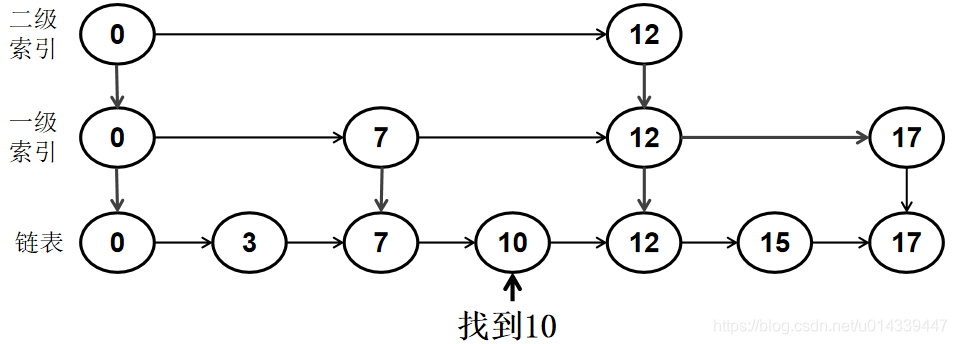
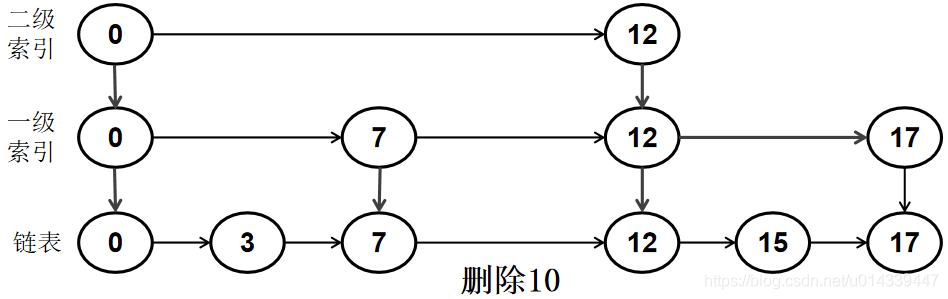
以上就是跳表的原理以及检索，插入，删除操作。

跳表具体怎么实现？

在实际实现时，为了方便操作，会给跳表添加头节点，头。跳表 0 -> 3 -> 7 -> 10 -> 12 -> 15 ->17 如下：

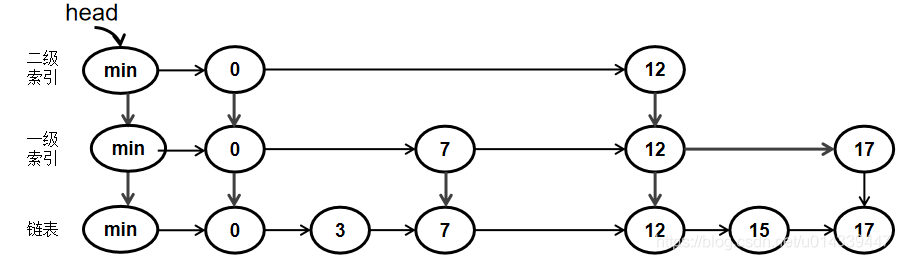
写下代码

#include <iostream>
#include <stack>
using namespace std;
class Node
{
public:
    int data;//数据
    Node* next;//后一个节点
    Node* down;//下方节点
    Node()//无参构造函数,节点值为最小值
    {
        data = INT_MIN;
        next = nullptr;
        down = nullptr;
    }
    Node(int x)//节点值为x
    {
        data = x;
        next = nullptr;
        down = nullptr;
    }
};

class SkipList
{
public:
    Node* head;//头指针
    SkipList()//初始化，头指针指向头节点
    {
        Node* minData = new Node();//头节点的值为 int 的最小值
        head = minData;
    }

bool search(int x)
{
    Node* p = head;
    while (p)
    {
        if (p->data == x)//找到x
            return true;
        else if (p->next == nullptr)//右侧没有节点
        {
            p = p->down;//向下
        }
        else if (p->next->data > x)//右侧节点值大于x
        {
            p = p->down;//向下
        }
        else
        {
            p = p->next;//向右
        }
    }
    return false;
}

void remove(int x)
{
    Node* p = head;
    while (p)
    {
        if (p->next == nullptr)//右侧没有节点
            p = p->down;//向下
        else if (p->next->data > x)//右侧节点值大于x
            p = p->down;//向下
        else if (p->next->data == x)//右侧节点值为x
        {
            p->next = p->next->next;//删除右侧节点
            p = p->down;
        }
        else
            p = p->next;//向后
    }
}

void insert(int x)
{
    if (search(x)) return;//链表中有x,不用重复插入
    stack<Node*> stkDown;//保存向下走过的节点，用于生成索引
    Node* p = head;
    while (p)
    {
        if (p->next == nullptr)//右侧没有节点
        {
            stkDown.push(p);//保存该节点，并向下走
            p = p->down;
        }
        else if (p->next->data > x)//右侧节点值大于x
        {
            stkDown.push(p);//保存该节点，并向下走
            p = p->down;
        }
        else
            p = p->next;//向右
    }

    Node* down = nullptr;//保存下方节点
    bool flag = true;//此标志保证原始链表一定要插入
    while (!stkDown.empty())
    {

        Node* pre = stkDown.top();//栈顶元素右侧可能要插入节点
        stkDown.pop();
        double num = (rand() % 11) / 10.;//生成随机数
        if (num > 0.5 || flag) {//如果随机数大于0.5或者是原始链表，则插如节点
            Node* newData = new Node(x);//生成新节点
            if (pre->next == nullptr)//插入到 pre 右侧
            {
                pre->next = newData;
                newData->down = down;
                down = newData;//保存新插入节点，索引中如果插入，需要指向该节点

            }
            else//插入到 pre 右侧
            {
                newData->next = pre->next->next;
                pre->next = newData;
                newData->down = down;
                down = newData;//保存新插入节点，索引中如果插入，需要指向该节点
            }
            flag = false;
        }
        else
            return;//如果随机小于 0.5 结束。
    }
    //通过随机数判断索引是否再上升一侧
    double num = (rand() % 11) / 10.;
    if (num > 0.5) {
        Node* newData = new Node(x);//节点 x
        Node* minData = new Node();//新索引头节点
        minData->down = head;//新索引生成。
        minData->next = newData;
        newData->down = down;
        head = minData;
    }
}

void print()
{
    Node* p = head;
    while (p)
    {
        Node* node = p->next;
        cout << "head:" << "->";
        while (node)
        {
            cout << node->data << "-->";
            node = node->next;
        }
        cout << endl;
        p = p->down;
    }
}
};

往期热文
什么是 Trie 树？
字符串查找—用16幅图从暴力一步步优化到KMP
面试高频：栈–3题多动图1模板讲明白
面试高频：双指针—6题14图一次搞懂