基础知识

整除

对于正整数 $n$，$m$，如果存在整数 $q$ 使得 $n = qm$，则称 $m$ 整除 $n$，记做 $m \mid n$。
称 $m$ 是 $n$ 的约数，$n$ 是 $m$ 的倍数。

最大公约数

对于正整数 $a$，$b$，若正整数 $d$ 满足 $d \mid a$ 且 $d \mid b$，则称 $d$ 是 $a$ 和 $b$ 的公约数。
$a$ 和 $b$ 最大的公约数称为 $a$，$b$ 的最大公约数，记做 $gcd(a, b)$ 或者 $(a, b)$。
$d$ 是 $a$，$b$ 的公约数等价于 $d \mid gcd(a, b)$。

互质

若正整数 $a$，$b$ 满足 $gcd(a, b) = 1$，则称 $a$ 与 $b$ 互质。
有时也记做 $a \bot b$。

取整函数

对于实数 $x$，记 $\left\lfloor x \right\rfloor$ 为不超过 $x$ 的最大整数。
$\left\lfloor x \right\rfloor$ 也是满足如下关系的唯一 函数：
$$\left\lfloor x \right\rfloor \leqslant x < \left\lfloor x \right\rfloor + 1$$

对于正整数 $n$，$1$ 到 $n$ 中 $d$ 的倍数有 $\left\lfloor \frac{n}{d} \right\rfloor$ 个。
我们时常要考虑形如 $\left\lfloor \frac{n}{d} \right\rfloor$ 的数。
为行文方便，后文可能会将这些数称为特殊点。（比如杜教筛）

性质

1. 对于任意的 $x$ 与正整数 $a$，$b$，我们均有：
   $$\left\lfloor \frac{\lfloor \frac{x}{a} \rfloor}{b} \right\rfloor = \lfloor \frac{x}{ab} \rfloor$$

2. 对于整数 $n$，考虑当 $1 \leqslant d \leqslant n$ 时，$\lfloor \frac{n}{d} \rfloor$ 的不同的取值个数。
   若 $d \leqslant \sqrt{n}$，则能得到的 $\lfloor \frac{n}{d} \rfloor$ 只有不超过 $\sqrt{n}$ 种。
   若 $d > \sqrt{n}$，则 $\lfloor \frac{n}{d} \rfloor \leqslant \frac{n}{d} \leqslant \sqrt{n}$，又因为 $\lfloor \frac{n}{d} \rfloor$ 是正整数，故此时可能的取值也不超过 $\sqrt{n}$ 种。
   综上，$\lfloor \frac{n}{d} \rfloor$ 可能的取值不超过 $2\sqrt{n}$ 种。（又称数论分块）

例题1

求
$$\sum_{d=1}^n \lfloor\frac{n}{d}\rfloor$$

$n \leqslant 10^{12}$。

对于 $\lfloor \frac{n}{d} \rfloor$ 的每个取值，对应的 $d$ 的范围是一个区间。枚举 $\lfloor\frac{n}{d}\rfloor$ 的取值即可。

附代码：

#include <bits/stdc++.h>

using std::cin;
using std::cout;
using ll = long long;

int main() {
    ll n;
    cin >> n;

    ll ans = 0;
    for (ll i = 1; i <= n; ++i) { // i为d的左端点，j为d的右端点
        ll t = n / i, j = n / t;
        ans += (j - i + 1) * t;
        i = j;
    }

    cout << ans << '\n';

    return 0;
}

调和数

调和数定义为 $H_n = \sum_{k=1}^n \frac{1}{k}$。
关于调和数有如下结论：
$$H_n = \ln n + \gamma + o(1)$$

这可以推出一个常见的时间复杂度：
$$\sum_{d=1}^n \lfloor \frac{n}{d} \rfloor = \Theta (n\log n)$$

素数

如果一个数 $p$ 的约数只有 $1$ 和 $p$ 自身，则称 $p$ 为素数。

算数基本定理

任意一个正整数 $n$ 都可以表示成素数的乘积的形式：
$$n = p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_s^{\alpha_s}$$
其中$p_1, \cdots, p_s$ 是不同素数。且不计次序的情况下，这一表达是唯一的。

求素数

求不超过 $n$ 的所有素数可以用 $O(n)$ 的 $Euler$ 筛法。
其思想是枚举每个数的最小素因子。

素数计数函数

令素数计数函数 $\pi(n)$ 表示不超过 $n$ 的素数个数。我们有如下的素数定理：
$$\pi(n) \sim \frac{n}{\ln n}$$

推论：

• $n$ 附近的素数密度近似是 $\frac{1}{\ln n}$
• 第 $n$ 个素数 $p_n \sim n\log n$

素数计数

显然可以利用 $Euler$ 筛算出 $n$ 以内的所有素数，进而得到 $\pi(n)$。
存在更快的做法。
用一种类似积性函数求和的筛法可以达到 $O(\frac{n^{\frac{3}{4}}}{\log n})$ 的复杂度。
先进的做法似乎可以达到 $O(\frac{n^{\frac{2}{3}}}{\log n})$。

数论函数

定义域为正整数、值域是复数的子集的函数称为数论函数。
但竞赛中研究的数论函数的值一般也是整数。

积性函数

• 设 $f$ 是数论函数，若对任意互质的正整数 $a, b$，都有 $f(ab) = f(a)f(b)$，则称 $f$ 是积性函数。

• 若对任意的正整数 $a, b$，都有 $f(ab) = f(a)f(b)$，则称 $f$ 是完全积性的。

• 若 $f$ 是积性函数，且 $n = p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_s^{\alpha_s}$ 是 $n$ 的标准分解， 则有

$$f(n) = f(p_1^{\alpha_1})f(p_2^{\alpha_2}) \cdots f(p_s^{\alpha_s})$$

因此研究积性函数 $f$ 可以转化为研究 $f(p^\alpha)$，即 $f$ 在素数和素数的幂上的取值。

积性函数求值

• 设 $f$ 是积性函数，为求 $f(n)$ 可以先对 $n$ 分解素因子，然后计算所有的 $f(p^{\alpha})$ 乘起来。
• 如果要对 $1$ 到 $n$ 之间的所有数求出 $f$，注意到 $Euler$ 筛法的过程中可以求出每个数的最小素因子和最小素因子的幂次，利用此就能在线性时间内计算出所需的 $f$ 的值。

单位函数

单位函数 $\varepsilon(n)$ 定义为：

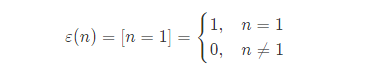
其中 [condition] 表示 condition 为真时取值为 $1$，否则为 $0$ 的函数。

单位函数是完全积性函数。

除数函数

除数函数 $\sigma_k(n)$ 用来表示 $n$ 的因子的 $k$ 次方之和：
$$\sigma_k\left( n \right) = \sum\limits_{\left. d \right|n} {{d^k}}$$

约数个数 $\sigma_0 (n)$ 常记为 $d(n)$，约数和 $\sigma_1 (n)$ 常记为 $\sigma(n)$。

除数函数都是积性涵数。

欧拉函数

$Euler$ 函数 $\varphi(n)$ 表示不超过 $n$ 且与 $n$ 互素的正整数的个数。

由 $n$ 的标准分解并结合容斥原理，我们可以得到 $n$ 的显式表达式 ：
$$\varphi \left( n \right) = n \cdot \prod\limits_{i = 1}^n {\left( {1 - \frac{1}{{{p_i}}}} \right)}$$
其中 $n = p_1^{{\alpha _1}}p_2^{{\alpha _2}} \cdots p_s^{{\alpha _s}}$ 是 $n$ 的标准分解。

由此易见 $Euler$ 函数是积性函数。

Euler 函数的性质

对于任意 $n$，$Euler$ 函数有如下性质：
$$n = \sum\limits_{\left. d \right|n} {\varphi \left( d \right)}$$

要证明这个等式，我们将 $1$ 到 $n$ 中的所有整数按与 $n$ 的最大公约数分类。
若 $gcd(n, i) = d$，那么 $gcd(\frac{n}{d}, \frac{i}{d}) = 1$。而又 $\frac{i}{d}$ 是不超过 $\frac{n}{d}$ 的整数，故这样的 $i$ 有 $\varphi(\frac{n}{d})$ 个。

考虑所有 $d \mid n$，我们也就考虑到了所有 $1$ 到 $n$ 之间的 $n$ 个整数，因此有
$$n=\sum\limits_{\left. d \right|n} {\varphi \left( {\frac{n}{d}} \right)} = \sum\limits_{\left. d \right|n} {\varphi \left( d \right)}$$

Dirichlet 卷积

设 $f, g$ 是数论函数，考虑数论函数 $h$ 满足
$$h\left( n \right) = \sum\limits_{\left. d \right|n} {f\left( d \right)g\left( {\frac{n}{d}} \right)}$$
则称 $h$ 为 $f$ 和 $g$ 的 $Dirichlet$ 卷积，记做 $h = f * g$。

Dirichlet 卷积的性质

• 单位函数 $\varepsilon$ 是 $Dirichlet$ 卷积的单位元，即对于任意函数 $f$，有 $\varepsilon * f = f * \varepsilon = f$。
  $Dirichlet$ 卷积满足交换律和结合律。
• 如果 $f, g$ 都是积性函数，那么 $f * g$ 也是积性函数。

许多关系都可以用狄利克雷卷积来表示。
下面用 $1$ 来表示取值为 $1$ 的常函数，定义幂函数 $I{d_k}\left( n \right) = {n^k},Id = I{d_1}$。

除数函数的定义可以写为：${\sigma _k} = 1*I{d_k}$

欧拉函数的性质可以写为：$Id = \varphi *1$

计算Dirichlet卷积

设 $f, g$ 是数论函数，计算 $f$ 和 $g$ 的 $Dirichlet$ 卷积在 $n$ 处的值需要枚举 $n$ 的所有约数。

如果要计算 $f$ 和 $g$ 的 $Dirichlet$ 卷积的前 $n$ 项，可以枚举 $1$ 到 $n$ 中每个数的倍数，根据调和数的相关结论，这样做的复杂度是 $O(n\log n)$。

Mobius 函数

$\color{blue}{Mobius}$ 函数 $\color{red}{\mu(n)}$ 定义为：
$$\mu(n) = \begin{cases} 1, & n = 1; \\\ (-1)^s, & n = p_1p_2 \cdots p_s; \\\ 0, & otherwise. \end{cases}$$

其中 $p_1, p_2, \cdots, p_s$ 是不同素数.
可以看出，$\mu(n)$ 恰在 $n$ 无平方因子时非零.
易见 $\color{red}{\mu}$ 是积性函数.

Mobius 函数的性质

$\color{blue}{Mobius}$ 函数具有如下最重要的性质：

$$\displaystyle \sum_{d \mid n} \mu(d) = \varepsilon(n)$$

使用 $\color{blue}{Dirichlet}$ 卷积来表示，即
$$\mu * 1 = \varepsilon$$

证明：

$n = 1$ 时显然成立。
若 $n > 1$，设 $n$ 有 $s$ 个不同的素因子，由于 $\mu(d) \neq 0$ 当且仅当 $d$ 无平方因子，故 $d$ 中每个素因子的指数只能为 $0$ 或 $1$。故有

$$\displaystyle \sum_{d \mid n} \mu(d) = \sum_{k = 0}^s (-1)^k \binom{s}{k} = (1 - 1)^s = 0$$

这就证明了 结论。

Mobius 变换

设 $f$ 是数论函数，定义函数 $g$ 满足

$$g(n) = \sum_{d \mid n} f(d) \tag{1}$$

则称 $g$ 是 $f$ 的 $\color{blue}{Mobius}$ 变换，$f$ 是 $g$ 的 $\color{blue}{Mobius}$ 逆变换。
用 $\color{purple}{Dirichlet}$ 卷积表示即为 $g = f * 1$。

Mobius 反演

$\color{blue}{Mobius}$ 反演定理指出，$(1)$ 的充要条件为：

$$f(n) = \sum_{d \mid n} g(n) \mu(\frac{n}{d}) \tag{2}$$

证明可以使用 $\color{purple}{\rm Dirichlet}$ 卷积：

$$g = f * 1 \Leftrightarrow f = f * \varepsilon = f * 1 * \mu = g * \mu$$

应用

利用 $\color{purple}{\rm Dirichlet}$ 卷积可以解决一系列求和问题。常见做法是使用一个 $\color{purple}{\rm Dirichlet}$ 卷积替换求和式中的一部分，然后调换求和顺序，最终降低时间复杂度。

经常利用的卷积有 $\mu * 1 = \varepsilon$ 和 $Id = \varphi * 1$。

无平方因子数

求 $n$ 以内无平方因子数的个数。亦即，求

$$\sum_{k = 1}^n \mu^2(k)$$

我们考虑一个素数 $p$，那么 $p^2$ 的倍数都有平方因子，个数是 $\lfloor \frac{n}{p^2} \rfloor$，应该从答案中去掉。
但是这样多去掉了一些数。比如对于不同的素数 $p_1, p_2, p_1^2p_2^2$ 的倍数就被去掉了两次，个数是 $\lfloor \frac{n}{p_1^2 p_2^2} \rfloor$，应该加回来。
显然这是容斥原理。

如果 $d$ 是 $s$ 个不同素数的乘积，那么其对答案的贡献是 $(-1)^s \lfloor \frac{n}{d^2} \rfloor$。
如果 $d$ 不是不同素数的乘积，即 $d$ 有平方因子，那么 $d$ 对答案没有贡献。
容斥的系数恰好是 $\color{blue}{\rm Mobius}$ 函数。

因此答案就是

$$\sum_{k=1}^n \mu^2(k) = \sum_{d = 1}^{\sqrt{n}} \mu(d) \lfloor \frac{n}{d^2} \rfloor$$

事实上，$\color{blue}{\rm Mobius}$ 反演本身就可以看成是对整除关系的容斥。
莫比乌斯反演是在有序偏序集上的容斥，容斥是莫比乌斯反演在有序偏序集上的实例。

数论函数求和

杜教筛

有一种利用 $\color{purple}{\rm Dirichlet}$ 卷积来构造递推式，从而对一些数论函数进行求和的方法。
民间称呼$\color{green}{杜教筛}$。
我们用两个例子来了解一下这个方法。

Euler 函数的前缀和

令

$$\phi(n) = \sum_{i = 1}^n \varphi(i)$$

我们考虑如何高速的求出 $\phi(n)$。

考虑到 $\rm Id = \varphi * 1$，我们有：

$$\begin{aligned} \frac{1}{2}n(n + 1) &= \sum_{k = 1}^n k = \sum_{k = 1}^n \sum_{d \mid k} \varphi(\frac{k}{d}) \\\ &= \sum_{d = 1}^n \sum_{1 \leqslant k \leqslant n \atop d \mid k} \varphi(\frac{k}{d}) \\\ &= \sum_{d = 1}^n \sum_{k = 1}^{\lfloor \frac{n}{d} \rfloor} \varphi(k) = \sum_{d = 1}^n \phi(\lfloor \frac{n}{d} \rfloor) \end{aligned}$$

我们可以得到：

$$\phi(n) = \frac{1}{2}n(n + 1) - \sum_{d = 2}^n \phi(\lfloor \frac{n}{d} \rfloor)$$

因此，如果对于 $2 \leqslant d \leqslant n$ 已经计算出了 $\phi(\lfloor \frac{n}{d} \rfloor)$，即特殊点处的函数值，由于特殊点不超过 $2\sqrt{n}$ 个，利用之前见过的分段的方法，我们可以在 $O(\sqrt{n})$ 的时间内计算出 $\phi(n)$。
而计算 $\phi(\lfloor \frac{n}{d} \rfloor)$ 是子问题，可以递归解决。
递归过程中会不会需要计算更多的函数值？
由特殊点的性质，可以发现所有要计算的就是所有特殊点处的函数值。
使用记忆化搜索，这样每个函数值只会被计算一遍。

时间复杂度分析

算法的时间复杂度就是计算所有特殊点处的函数值的时间复杂度。
回忆特殊点的结构，时间复杂度 $T(n)$ 可以估计为

$$T(n) = \sum_{i = 1}^{\sqrt{n}}O(\sqrt{i}) + \sum_{i = 1}^{\sqrt{n}}O\left(\sqrt{\lfloor \frac{n}{i} \rfloor}\right)$$

显然式中第一项渐进意义上小于第二项。

而对于式中第二项我们可以利用积分估计：

$$\sum_{i = 1}^{\sqrt{n}}O\left(\sqrt{\lfloor \frac{n}{i} \rfloor}\right) = O\left(\int_1^{\sqrt{n}} \sqrt{\frac{n}{x}}{\rm d} x\right) = O(n^{\frac{1}{2}} \cdot n^{\frac{1}{4}}) = O(n^{\frac{3}{4}})$$

于是算法的时间复杂度为 $O(n^{\frac{3}{4}})$。

注意到我们还可以使用 $\rm Euler$ 筛求出 $\varphi$ 的值，进而求出前缀和。

假设我们使用 $\rm Euler$ 筛预先求出了 $\varphi$ 的前 $S$ 项，那么递归部分的时间复杂度变为：

$$\sum_{i = 1}^{\frac{n}{S}} O\left(\left\lfloor \frac{n}{i} \right\rfloor\right) = O\left(\int_1^{\frac{n}{S}} \sqrt{\frac{n}{x}} {\rm d} x \right) = O\left(n^{\frac{1}{2}} \cdot \sqrt{\frac{n}{S}}\right) = O\left(\frac{n}{S^{\frac{1}{2}}}\right)$$

结合 $\rm Euler$ 筛的时间复杂度 $O(S)$，总的时间复杂度为 $O(S + \frac{n}{S^{\frac{1}{2}}})$。

如果取 $S = n^{\frac{2}{3}}$，那么总的时间复杂度为 $O(n^{\frac{2}{3}})$。

#include <cstdio>

typedef long long ll;

const ll XN = 1000000000, XR = 1000031;

bool ip[XR];
int p[XR / 10], c = 0;
ll phi[XR], sphi0[XR];

ll sphi[XN / XR + 100];

ll n = 1000000000;

// 预处理2/3 
void sieve() {
    ip[0] = ip[1] = 1;
    phi[1] = 1;
    for (int i = 2; i < XR; ++i) {
        if (!ip[i]) p[c++] = i, phi[i] = i - 1;
        for (int j = 0; j < c and i * p[j] < XR; ++j) {
            ip[i * p[j]] = 1;
            if (i % p[j]) phi[i * p[j]] = phi[i] * (p[j] - 1);
            else {
                phi[i * p[j]] = phi[i] * p[j];
                break;
            }
        }
    }
    for (int i = 1; i < XR; ++i) sphi0[i] = sphi0[i - 1] + phi[i];
}

ll calc(ll k) {
    if (k < XR) return sphi0[k];
    else {
        auto &z = sphi[n / k];
        if (!z) {
            z = k * (k + 1) / 2;
            for (ll i = 2; i <= k; ++i) {
                ll t = k / i, j = k / t;
                z -= (j - i + 1) * calc(t);
                i = j;
            }
        }
        return z;
    } 
}

int main() {
    sieve();
    printf("%lld\n", calc(n));
    return 0;
}

Mobius 函数的前缀和

令

$$M\left( n \right) = \sum\limits_{k = 1}^n {\mu \left( k \right)}$$

计算的过程与 $\varphi$ 是类似的。不过这次需要使用 $\mu * 1 = \varepsilon$。

$$\begin{aligned} 1 &= \sum_{k = 1}^n \varepsilon(k) = \sum_{k = 1}^n \sum_{d \mid k} \mu(\frac{k}{d}) \\\ &= \sum_{d = 1}^n \sum_{1 \leqslant k \leqslant n \atop d \mid k} \mu(\frac{k}{d}) = \sum_{d = 1}^n \sum_{k = 1}^{\lfloor \frac{n}{d} \rfloor} \mu(k) = \sum_{d = 1}^n M(\lfloor \frac{n}{d} \rfloor) \end{aligned}$$

于是可以得到

$$M(n) = 1 - \sum_{d = 2}^n M\left(\left\lfloor\frac{n}{d}\right\rfloor\right)$$

用同样的方法递推即可。

一般化

在求 $\varphi$ 和 $\mu$ 的前缀和的过程中，我们都利用了一个 $\color{purple}{\rm Dirichlet}$ 卷积。

这就让我们考虑数论函数 $f, g$ 的前缀和与它们的 $\color{purple}{\rm Dirichlet}$ 卷积 $f*g$ 的前缀和之间的关系。

用 $F$ 表示 $f$ 的前缀和，我们有

$$\begin{aligned} \sum_{k = 1}^n (f * g)(k) &= \sum_{k = 1}^n\sum_{d \mid k} f(\frac{k}{d})g(d) \\\ &= \sum_{d = 1}^n\sum_{1 \leqslant k \leqslant n \atop d \mid k} g(d)f(\frac{k}{d}) = \sum_{d = 1}^n g(d)\sum_{k = 1}^{\lfloor \frac{n}{d} \rfloor}f(k) \\\ &= \sum_{d = 1}^n g(d)F(\lfloor \frac{n}{d} \rfloor) \end{aligned}$$

在上两例中，$f*g$ 和 $g$ 的前缀和都可以 $O(1)$ 得出，因此 $f$ 可以用杜教筛计算。
其实并不需要如此强的性质。

可以看到，在杜教筛的过程中，我们实际上求出了所有特殊点处的前缀和。
注意到 $g$ 的前缀和是对使得 $\lfloor \frac{n}{d} \rfloor$ 相同 $d$ 分段的时候用到的，因此只需要用到 $g$ 在段落端点处的前缀和。
可以发现，段落的端点恰好是所有的特殊点。

因此，$f, g$ 以及 $f*g$ 这三个函数中，只要有两个可以用不弱于杜教筛的方法求值，就可以杜教筛第三个。

约数个数求和

求

$$\sum_{k = 1}^n \sigma_0 (k)$$

杜教筛？

$$\sum_{k = 1}^n \sigma_0 (k) = \sum_{k = 1}^n \sum_{d \mid k} 1 = \sum_{d = 1}^n \lfloor \frac{n}{d} \rfloor$$

一些练习题：

1. Longge 的问题
2. 仪仗队
3. 幽灵乐团 / 莫比乌斯反演基础练习题
4. Crash的数字表格 / JZPTAB
5. 数表
6. 旧试题
7. 古代猪文
8. 能量采集
9. 完全平方数
10. ZAP-Queries
11. YY的GCD
12. 约数个数和
13. Problem b
14. 循环之美