$\Huge\color{orchid}{点击此处获取更多干货}$

组合数在考研中的重要性主要体现在概率论中“离散型随机变量”部分，以及数据结构中出栈序列可能涉及的“卡特兰数”，这两类问题在各算法类网站上都能见到，因此本帖将用两节，详细分析用程序求组合数的常用方法。

首先，回顾一下高中数学，组合数的公式如下：
$$C_{n}^{m} = \frac{A_{n}^{m}}{A_{m}^{m}}=\frac{n!}{m!*(n-m)!}=\frac{\prod_{i=1}^{m}(n+1-i) }{\prod_{i=1}^{m} i}（其中n,m是整数，n\ge m）$$

那么，组合数非常显而易见的一个求法就是硬算：

template <class _Ty>
_Ty combine(int n, int m) {
    _Ty ans = _Ty(1);
    while (m > 0) {   //循环过程中可以同时处理分子分母
        ans = ans * (n + 1 - m) / m;
        m--;
    }
    return ans;
}

模板函数$\text{combine}$中，模板参数$\text{_Ty}$可视情况选择各种整数类型（$\text{int,long long甚至size_t)}$，如果还不够的话可以用高精度运算方法实现$\text{BigInteger}$类（点击最上面的粉色字可以回顾高精度运算）

在不用$\text{BigInteger}$的情况下如果涉及取模，为了防止溢出，每一次乘法或除法之后都需要对一个数$P$取模（$P$大概率是质数），那么在除以$m$的时候，就需要求$m$在模$P$意义下的乘法逆元。在$P$为质数的情况下，直接用“乘以$m^{P-2}$”替代“除以$m$”即可，在$P$较大的情况下，幂运算可以用快速幂算法。（以下所有方法，全部都用$\text{size_t}$来替代模板参数$\text{_Ty}$）

size_t quickPower(size_t base, size_t power, size_t mod) {
    size_t ans = 1;
    while (power > 0) {
        if (power & 1) ans = (ans * base) % mod;
        base = (base * base) % mod;
        power >>= 1;
    }
    return ans;
}

size_t combine(size_t n, size_t m, size_t p) {
    size_t ans = 1;
    while (m > 0) {
        ans = (ans * (n + 1 - m)) % p;    //防溢出，每次运算后都要取模
        ans = (ans * quickPower(m, p - 2, p)) % p;
        m--;
    }
    return ans;
}

如果直接从阶乘式入手，除了硬算之外，还可以将阶乘转化为少数几个质数的幂运算，这里需要借助算术基本定理，即任何一个大于1的正整数都可以分解成若干质因数的乘积，因此$n$的阶乘就相当于$2\sim n$中每个数的质因数相乘所得的结果，其中每个质因数$p$出现的次数为$2\sim n$中每个数产生的$p$的数量，可以用无穷级数$\sum_{i=1}^{+\infty } \lfloor \frac{n}{p^i} \rfloor$来表示。到这里可能有人会有疑问：为什么不是$\sum_{i=1}^{+\infty } i*\lfloor \frac{n}{p^i} \rfloor$呢？下面以$16!$中$2$的出现次数为例来解释。

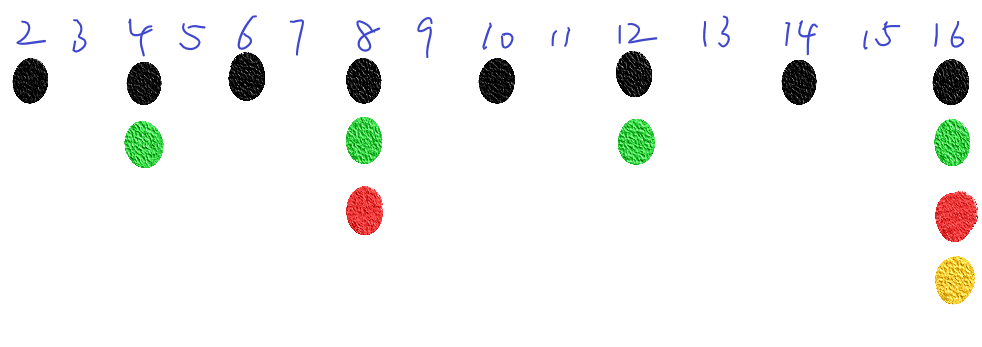
$2\sim 16$之间所有的整数包含因数$2$的个数，显然为$15$，其中包含$1$个$2$的有$\{2,6,10,14\}$，包含$2$个$2$的有$\{4,12\}$，包含$3$个$2$的只有$8$，而包含$4$个$2$的只有$16$，累加起来即为$1*4+2*2+1*3+1*4=15$，可以完美的对应上级数$\sum_{i=1}^{+\infty } i*\lfloor \frac{n}{p^i} \rfloor$，其中的每个$i$都代表“刚好”包含$i$个因数$p$的整数个数。而另一个级数$\sum_{i=1}^{+\infty } \lfloor \frac{n}{p^i} \rfloor$中，每个$i$则与“至少”包含$i$个因数$p$相互对应。至少包含$i$个因数$p$就代表着一个数是$p^i$的倍数，比如$2\sim 16$之间，$2$的倍数有$8$个，$4$的倍数有$4$个，$8$的倍数有$2$个，$16$的倍数有$1$个另外如果一个数至少含有$k$个因数$p$，那么它一定会至少含有$1,2,…,k-1$个因数$p$。以上图中的$16$为例，它在被$i=4$计算到时，在$i=1,2,3$时一定都会被计算到一次，所以每一轮只需要计算一次。用“至少”的思路去计算，每一轮的目标都是均匀分布，累加的数量呈现$\frac{1}{p}$递减趋势，而用“恰好”的思路去计算，那么每轮的目标分布相对散乱，累加起来比较复杂。

上述的思路基于的是级数$\sum_{i=1}^{+\infty } \lfloor \frac{n}{p^i} \rfloor$，它不仅可以视作分母依次乘$p$，还可以视作分子依次除$p$，为防止溢出，此处采用分子依次除$p$的方式：

size_t countPrimeFactor(size_t n, size_t p) {
    size_t cnt = 0;
    while (n > 0) {
        cnt += n / p;   //整数除法自动向下取整
        n /= p;
    }
    return cnt;
}

解决了质因数统计的问题之后，还有一个需要注意的地方，那就是组合数$C_n^m$计算的阶乘式中，最大的项为$n!$，因此只有不大于$n$的质数才会对结果产生影响。所以在统计之前，还需要做的一件事就是筛选出不大于$n$的质数，这里可以使用欧拉筛（$\text{EulerSieve}$）。
从阶乘入手，分解质因数的方法，完整函数代码如下：

size_t combine(size_t n, size_t m, size_t p) {
    size_t ans = 1;
    Sieve* sieve = new EulerSieve;
    int len = (*sieve)(n);                      //n一定大于m和n-m，只要筛一次就行
    for (int i = 0; i < len; i++) {
        size_t x = sieve->primes[i];            //待统计的质因数
        size_t cnt = countPrimeFactor(n, x)     //出现在分母上的m!和(n-m)!需要对应相减
            - countPrimeFactor(m, x)
            - countPrimeFactor(n - m, x);
        ans = (ans * quickPower(x, cnt, p)) % p;//继续使用逆元法中的快速幂
    }
    delete sieve;
    return ans;
}

除了从公式直接入手以外，组合数还有两个重要性质，这两个性质同样可以用于组合数的求解，详情请见下节