字典树
有时候我们需要维护每个字符串的存在情况和出现次数,而字符串之间的比较的操作耗时是与长度相关的,用二分查找的话
可能会造成大量时间浪费。
我们可以为字符串设计一种专用的树形数据结构——字典树(trie)。
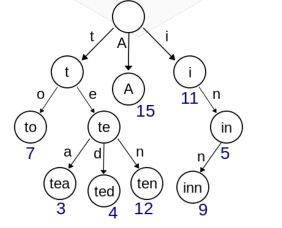
上图是一个保存了8个键的字典树结构:
“A”, “to”, “tea”, “ted”, “ten”,
“i”, “in”, “inn”,
代码实现
字典序中的每个结点需要保存对应字符串的出现次数,以及若干个指向儿子的指针。儿子指针的数量取决于字符集的大小。
struct trie {
int cnt;
trie *son[128];
};
建立根节点,表示空串。
trie *root = new trie();
插入一个字符串s的时候,扫描字符串的同时沿着树中的链向下走。
如果下一步要走到的结点还不存在,就新建结点。
void insert(char *s) {
trie *p = root;
while (*s != '\0') {
if (p->son[*s] == NULL)
p->son[*s] = new trie();
p = p->son[*s];
s++;
}
p->cnt++;
}
查询一个字符串的时候也是同样的,沿着树上路径一步步走即可。
如果走到了 NULL,则说明正在查询的字符串不存在。
int search(char *s) {
trie *p = root;
while (p != NULL && *s != '\0')
p = p->son[*s], s++;
if (p != NULL)
return p->cnt;
return 0;
}
字典树还有以下应用:
- 给字符串排序(遍历字典树)
- 快速地求两个字符串的最长公共前缀(树上最近公共祖先)
- 基于字典树构建 AC 自动机
板子
// 字符Trie
class Trie {
private:
vector<Trie*> children;
bool isEnd;
Trie* searchPrefix(string prefix) {
Trie* node = this;
for (char ch : prefix) {
ch -= 'a';
if (node->children[ch] == nullptr) {
return nullptr;
}
node = node->children[ch];
}
return node;
}
public:
Trie() : children(26), isEnd(false) {}
void insert(string word) {
Trie* node = this;
for (char ch : word) {
ch -= 'a';
if (node->children[ch] == nullptr) {
node->children[ch] = new Trie();
}
node = node->children[ch];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this->searchPrefix(word);
return node != nullptr and node->isEnd;
}
bool startsWith(string prefix) {
return this->searchPrefix(prefix) != nullptr;
}
};
// 01 Trie
const int K = 60;
struct Trie {
vector<int> l, r, c;
Trie(): l(1, -1), r(1, -1), c(1, 0) {}
int newNode() {
int i = l.size();
l.push_back(-1);
r.push_back(-1);
c.push_back(0);
return i;
}
int getNext(int i, int a, bool read=true) {
if (a == 0) {
if (l[i] == -1 and !read) {
int ni = newNode();
l[i] = ni;
}
return l[i];
}
else {
if (r[i] == -1 and !read) {
int ni = newNode();
r[i] = ni;
}
return r[i];
}
}
void add(ll x) {
int i = 0;
c[0]++;
for (ll b = 1ll<<K; b; b >>= 1) {
int a = (x&b) ? 1 : 0;
i = getNext(i, a, false);
c[i]++;
}
}
int count(ll x) { // count <= x
int i = 0, res = 0;
for (ll b = 1ll<<K; b; b >>= 1) {
int a = (x&b) ? 1 : 0;
if (a == 1) {
if (l[i] != -1) res += c[l[i]];
}
i = getNext(i, a);
if (i == -1) return res;
}
res += c[i];
return res;
}
ll getKth(int k) {
if (k <= 0 or c[0] < k) return -1;
int i = 0;
ll res = 0;
for (ll b = 1ll<<K; b; b >>= 1) {
if (l[i] != -1 and c[l[i]] >= k) {
i = l[i];
}
else {
k -= c[l[i]];
i = r[i];
res |= b;
}
}
return res;
}
};

