因为我也是一名菜鸡，刚刚初学没几天。
所以可能会出现表达错误，理解错误等一系列的问题。。希望各位大佬轻轻喷
同时欢迎在评论区指出有错误的地方~谢谢各位

dijkstra的主要思想：在每次寻找路径时，寻找当前节点与当前节点直接连接的节点之间最短的路径

这样可以保证每两个点之间的路径是最小的，以此来达到从源点到终点的距离是最小的

也正因为如此，所以dijkstra不能寻找存在负权边的情况——会有曲线救国的情况发生

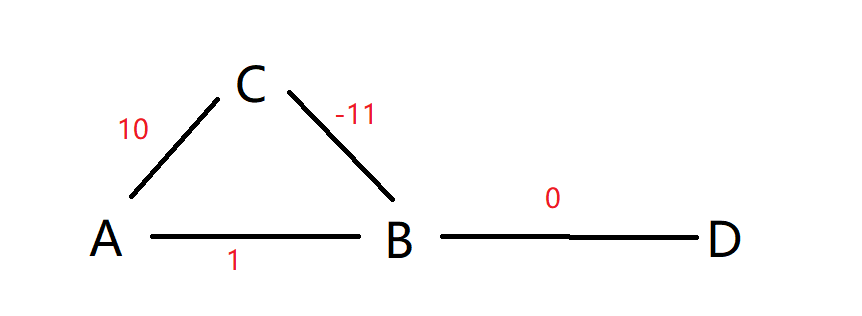
看这张图
不用 dijkstra算法，以咱们人的角度来看 最短路是 A C B D 最后结果为-1
使用dijkstra算法 结果是 A B D 最后结果为1
明显dijkstra是有问题的，问题在哪？——节点B上

咱们来看一下dijkstra的运行流程
这里的 1 2 3 4 分别对应A B C D

为了看的直观 我把节点改为字母

4 4
1 2 1
2 4 0
1 3 10
3 2 -11
节点A，距离0出队
节点A，已经加入集合st
节点C，距离10入队
节点B，距离1入队
节点B，距离1出队
节点B，已经加入集合st
节点D，距离1入队
节点D，距离1出队
节点D，已经加入集合st
节点C，距离10出队
节点C，已经加入集合st
节点B，距离-1入队
节点B，距离-1出队
1

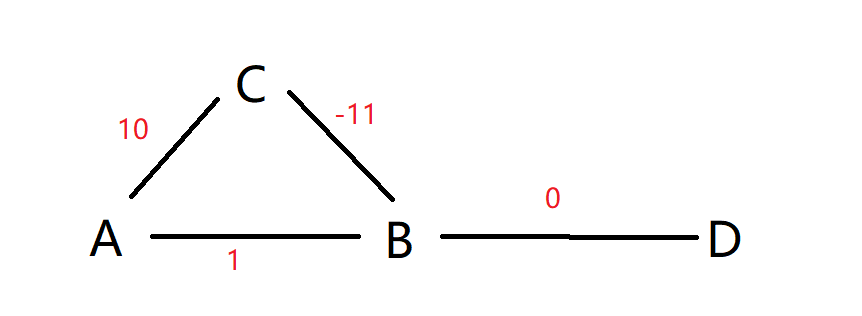
A 节点有两个分支 节点B 和C。在这两个分支节点中，节点B的距离是最短，所以在优先队列中，B节点先出来，同时B节点进入集合S中，此时从源点A到节点B的距离是1（问题就在这里）

然后咱们来看节点C，从A到C的距离是10，C到B的距离是-11.
这样 A->C->B最终到达B点的距离是-1，比之前从A到B的距离要小，此时节点B,距离源点A的距离为-1已经入队。(也就是上面运行结果的最后两行)
但是这里会有一个问题，在B出队时，会检测B是否在集合s中，这里走经过C这条路，到B的距离确实比之前要小，但是B已经进入过集合s中了，碰到判断语句会直接continue。
if (st[poi]) continue; st[poi] = true;
然后到B的距离就无法更新成-1.
所以最终答案 只能为1

最后贴上代码
(就是稀疏图使用的代码，加了几个print语句来展示每个状态的情况)

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 2e5 + 10;
int e[N], ne[N], h[N], idx, w[N],d[N];
int n, m;
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx++;
}

int dijkstra()
{
    memset(d, 0x3f, sizeof d);
    d[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({ 0,1 });

    while (heap.size())
    {
        PII t = heap.top();
        heap.pop();

        int poi = t.second, dist = t.first;
        printf("节点%d，距离%d出队\n", poi,dist);
        if (st[poi]) continue;
        st[poi] = true;
        printf("节点%d,已经加入集合st\n", poi);
        for (int i = h[poi]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (d[j] > dist + w[i])
            {
                d[j] = dist + w[i];
                heap.push({ d[j],j });
                printf("节点%d，距离%d入队\n", j,d[j]);
            }
        }
    }
    if (d[n] == 0x3f3f3f3f) return -1;
    return d[n];
}


int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;

    for (int i = 0; i < m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    printf("%d", dijkstra());
}