概述
现在有一个问题就是有北京—>成都选什么路径使时间花费最少?或者同时求北京---->海南,天津—>石家庄?当然我给你全国的路线,我们一般是枚举选最少的!现在我们来看一下怎么样用高效的算法去解决!
解决最短路径问题有几个优秀的算法:
1.dijkstra算法,最经典的单源最短路径算法
2.bellman-ford算法,允许负权边的单源最短路径算法
3.spfa,其实是bellman-ford+队列优化,其实和bfs的关系更密一点
4.floyd算法,经典的多源最短路径算法
我们来看一下yxc老师的知识结构图:
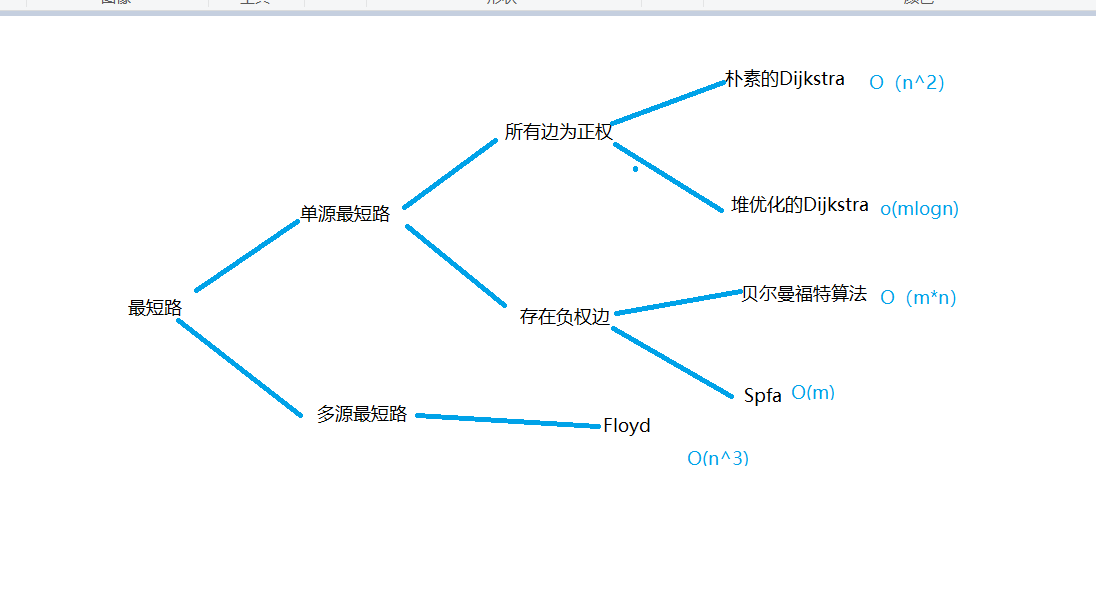
下面我们来开始一个一个认识:
Dijkstra
Dijkstra 算法,用于对有权图进行搜索,找出图中两点的最短距离,既不是DFS搜索,也不是BFS搜索。
把Dijkstra 算法应用于无权图,或者所有边的权都相等的图,Dijkstra 算法等同于BFS搜索。
首先我们来看一下它能干什么:
能解决源点到任意一个点的距离(就是有北京到全国各地的最短时间路程规划)
算法的思路:
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了)第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
简单来说就是:
1. 先定义dist[1]=0,dist[i]=INF;
2. for 1~n i判断不在S中,且距离最近的点,把他加入s中
3. 然后开始更新一下它到其他点的距离
如果觉得麻烦就看一个动态图:
其实一句话来说就是,对于全国路线网,你要确定北京为起点,然后根据路线图来现在最优路线!
我们来举一个例子:
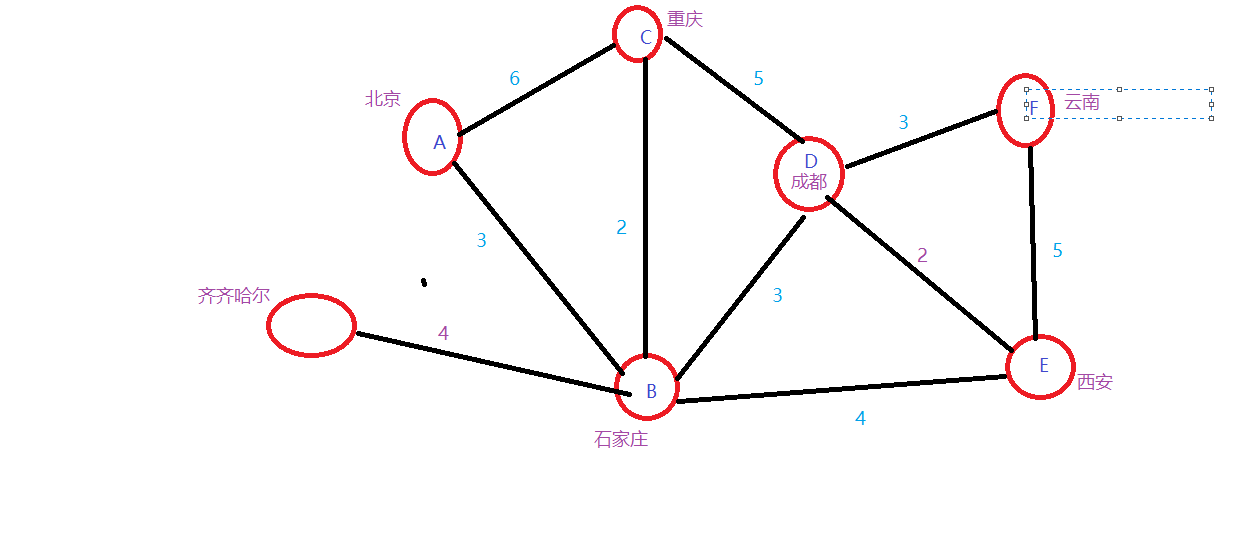
1.创建一个dist[]数组用于存储距离,先将他们初始化为INT_MAX,一个给g图数组!然后开始从A开始搜索:
为了方便为定义灰色将要处理,黑色已经处理!
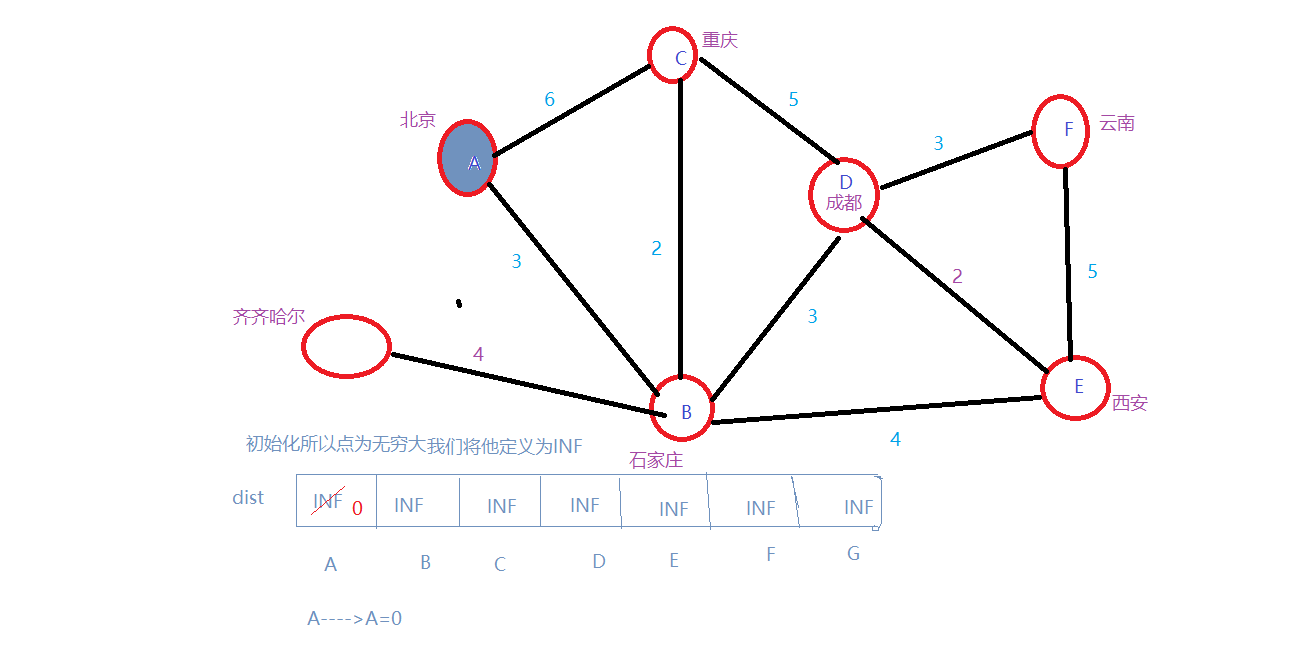
2.A–>A=0,现在有A的最短路径A–A=0,A–>B=3
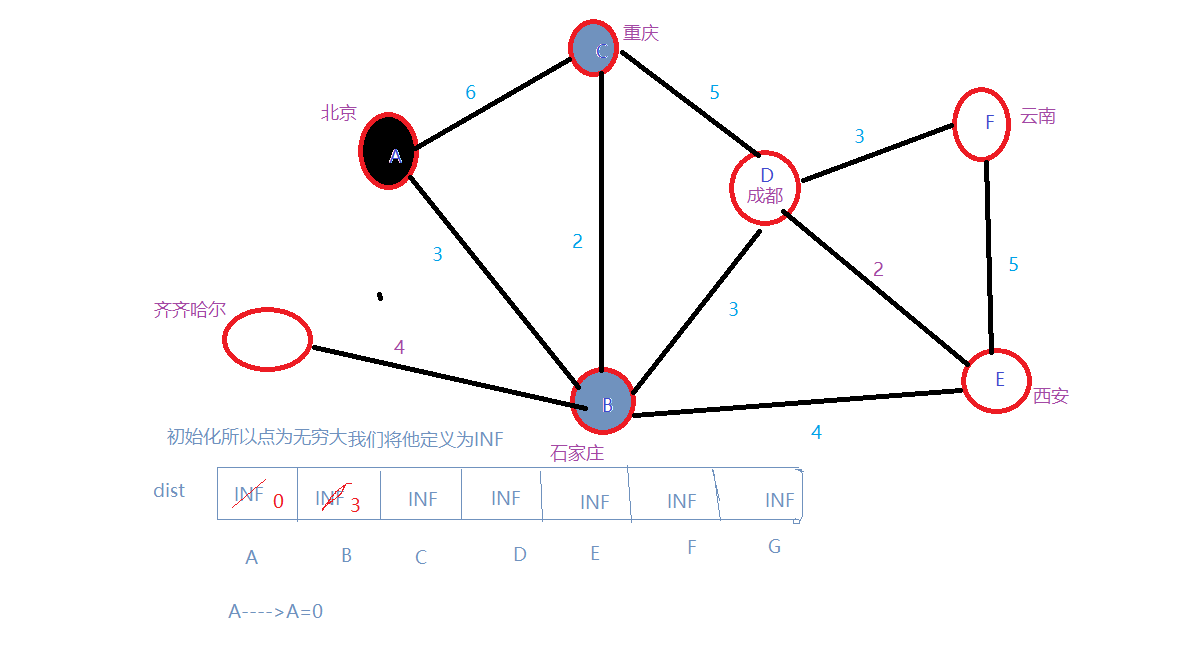
3.然后选入C,此时有最短路A–>A=0,B=3,C=5;
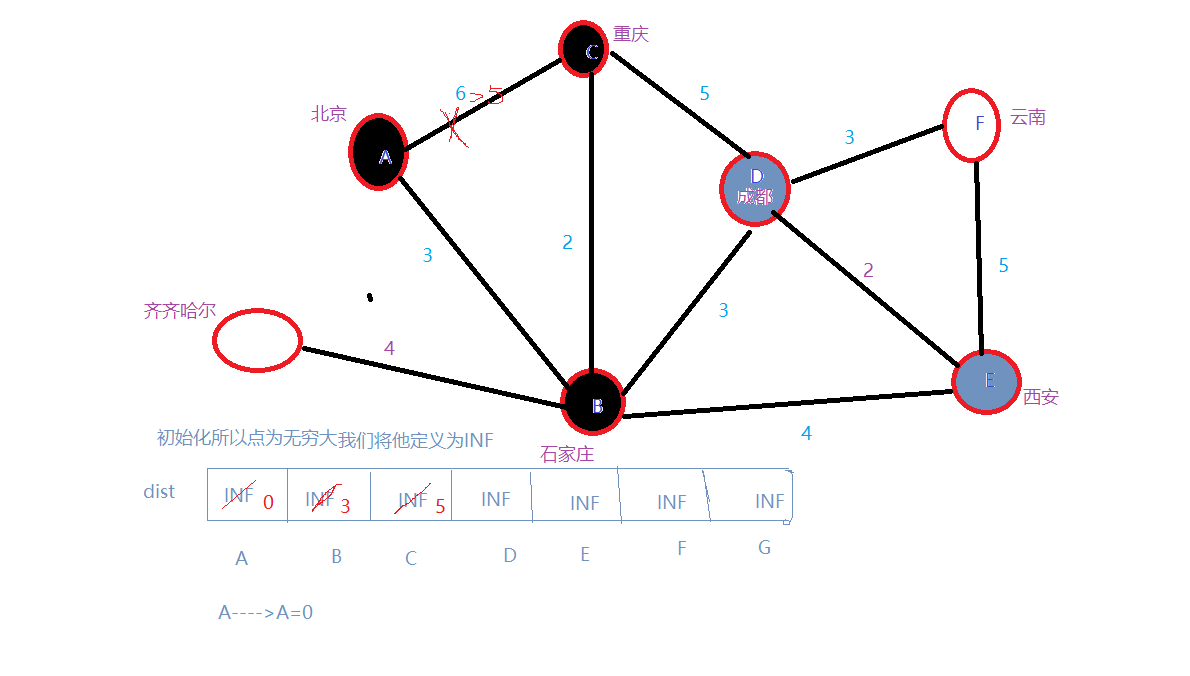
4.选入D,进行权重比较就有了,A–>B–>D=6最短
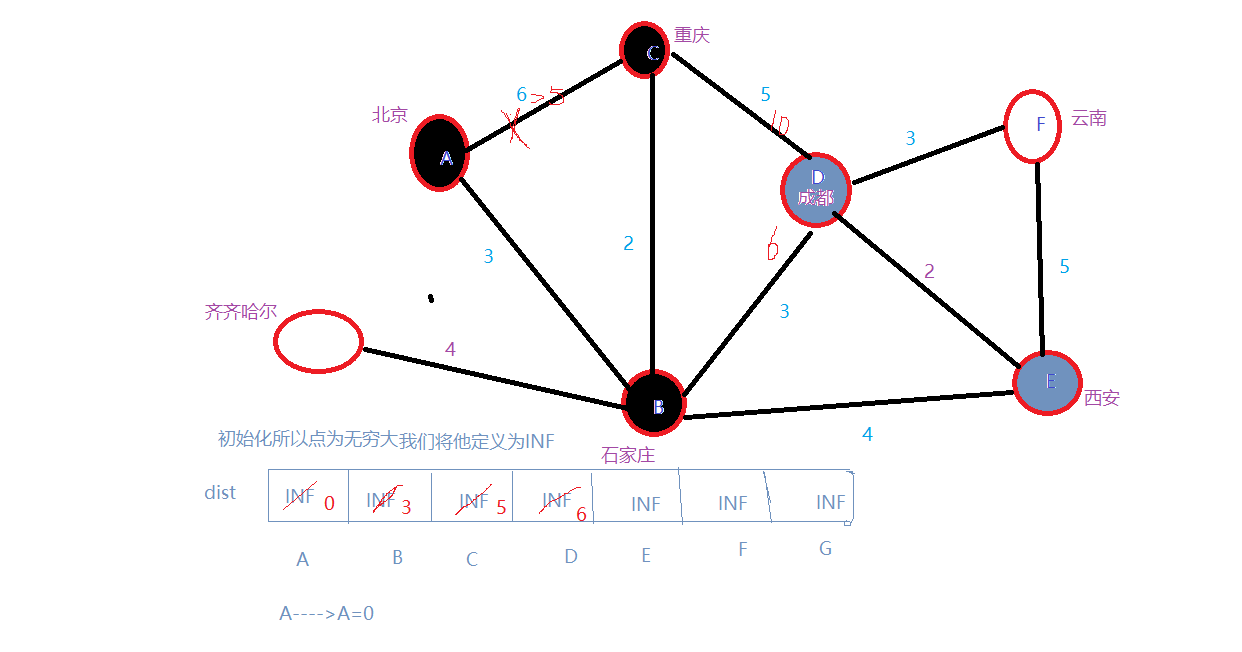
5.选入E,A–>c–>E=7最短
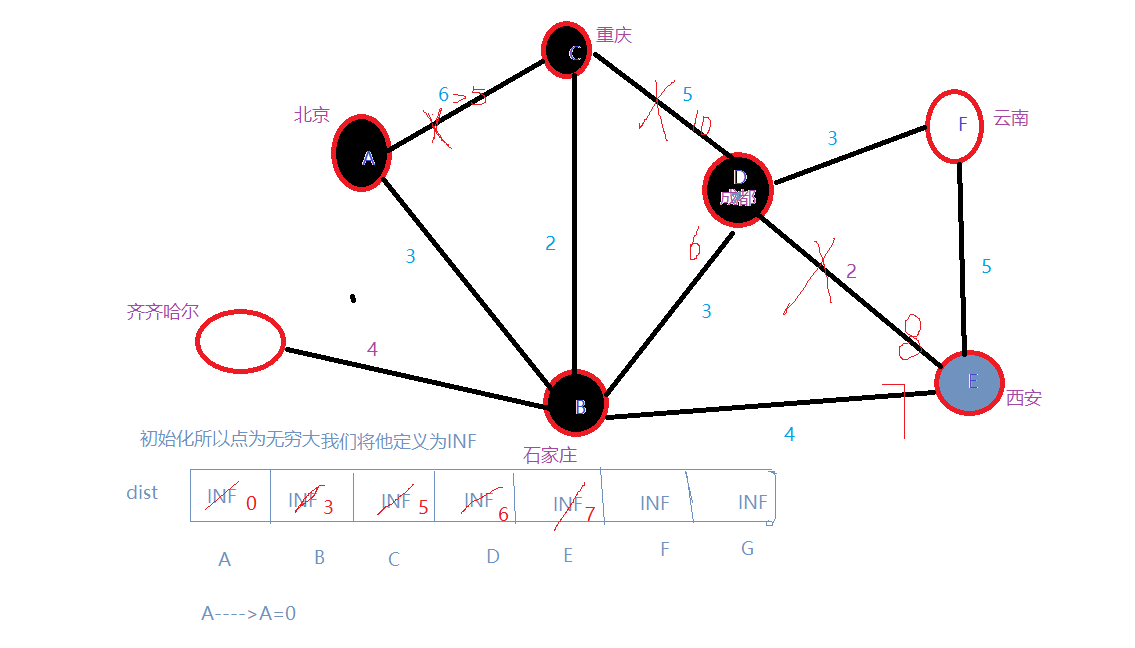
6.选入F,A->b->D–>F=9最短
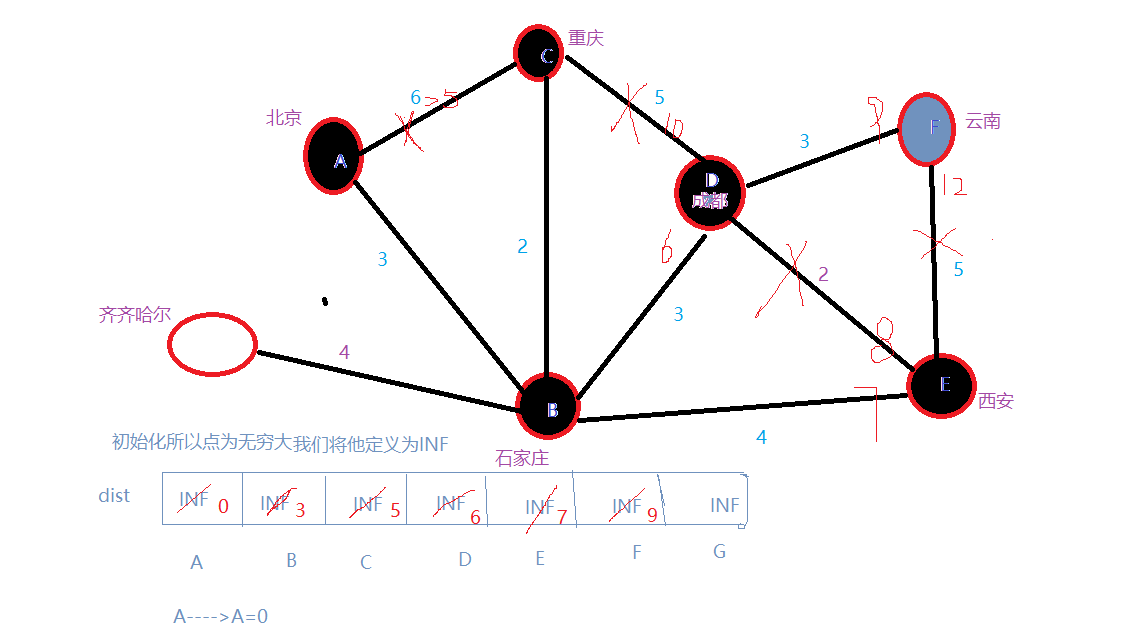
7.选入齐齐哈尔,但是没有相应的路径,所以A–>齐齐哈尔=INF
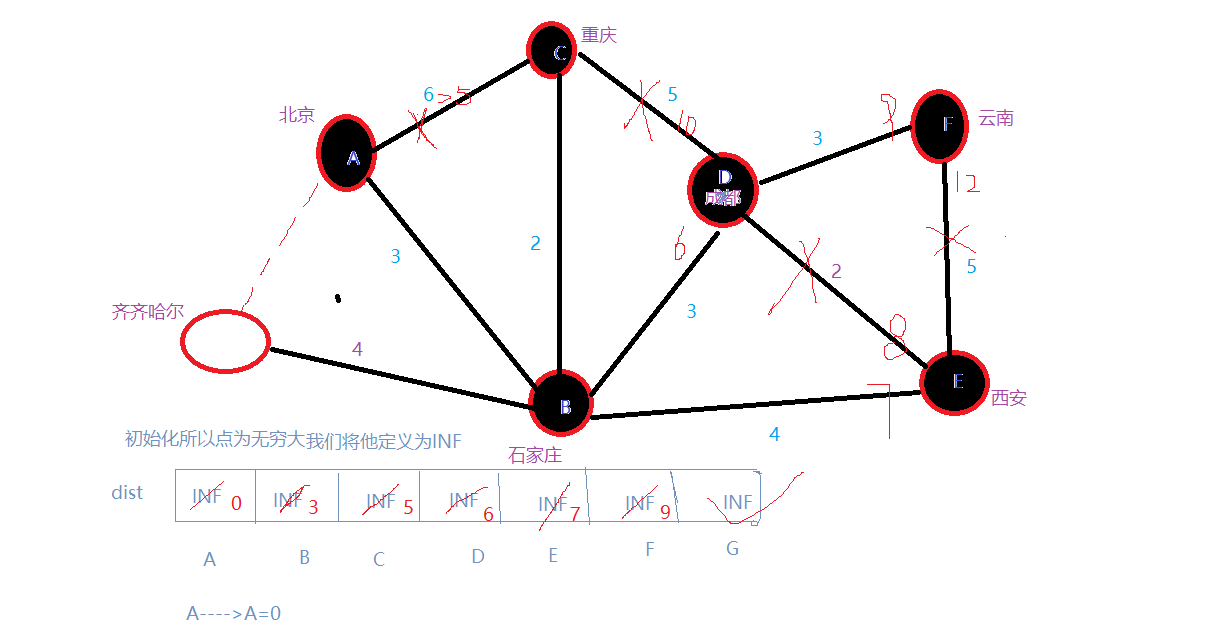
8.由于图中的点已经全部松弛,所以结束!
如果你对得到最短路径有疑问!我来解释一段:就以选入B来说,选入B,那么图里面就要去除这个点,我们发现A–>B—>B=5,A–>B–>D=6,A–>B–>E=7,A–>B–>其他点为INF,所以最短路径就是A–B–C=5;其他点也是这样类似计算!
实例中我们可以发现,Dijkstra 算法是一个排序过程,就上面的例子来说,是根据A到图中其余点的最短路径长度进行排序,路径越短越先被找到,路径越长越靠后才能被找到,要找A到F的最短路径,我们依次找到了
(A,B)A –> B 的最短路径 3
(A,C)A –> B –> C 的最短路径 5
(A,D)A –> B –> D 的最短路径 6
(A,E)A –> B –> E 的最短路径 7
(A,F)A –> B –> D –> F 的最短路径 9
(A,G)A-______-G=INF;
好了算法具体我们已经理解了:
我们来看一个例题:
习题
习题链接
分析:
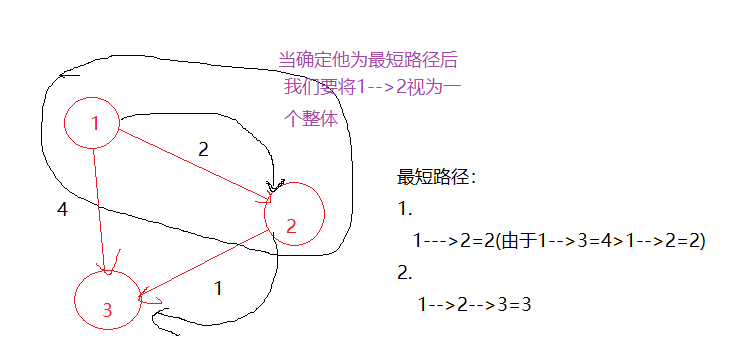
代码:
int dijkstrac(){
memset(dist,0x3f,sizeof dist);
//初始化
dist[1]=0;
//设置A-->A=0开始距离
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++)
//寻找
if(!st[j]&&(t==-1||dist[j]<dist[t]))
t=j;
st[t]=true;
//最优路径
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
if(dist[n]==0x3f3f3f3f)return -1;
return dist[n];
}
真正想理解的快就自己画一个图,按照代码一步一步走!
代码一眼看过去你根本不知道那是干嘛,甚至有可能你还不清楚参数的含义!好了,看来模板之后,你可能会发现他居然是O(n^2)的算法,她有没有可能优化呢?
我们知道我们是寻找最小的数,而且寻找会要删除该点,然后向后移动,我们可以想到用最小优先队列实现,当然我可以用书写队列(太过于复杂不建议运用)!而且时间复杂度是O(nlogn)n代表边数,m是点数,他一般用于稀疏图,而朴素的Dijkstra用于稠密图!
我们还是看代码理解吧:
int dijkstra(){
memset(dist,0x3f,sizeof dist);
//初始化
dist[1]=0;
//起点选定
priority_queue<PII,vector<PII>,greater<PII> >heap;
//定义一个小根堆
heap.push({0,1});
while(heap.size()){
auto t=heap.top();
heap.pop();
int ver=t.second,distance=t.first;
if(st[ver])continue;
//开始循环查找
for(int i=h[ver];i!=-1;i=ne[i]){
int j=e[i];
//如果距离大了,选择最小路径
if(dist[j]>distance+w[i]){
dist[j]=distance+w[i];
heap.push({dist[j],j});
}
}
}
if(dist[n]==0x3f3f3f3f)return -1;
return dist[n];
}
bellman-ford
我们知道Dijkstrac有不能有负权的边缺陷,而贝尔曼福特算法就可以解决它!当然还不止他一个算法可以处理负权问题!相比Dijkstrac,它的边的权值可以为负数、实现简单,而还可以限定边数,缺点是时间复杂度过高,高达O(n*m)。但算法可以进行若干种优化,提高了效率。
下面我们来看一下这个算法:
可用于解决以下问题:
从A出发是否存在到达各个节点的路径(有计算出值当然就可以到达);
从A出发到达各个节点最短路径(时间最少、或者路径最少等)
图中是否存在负环路(权重之和为负数)
其思路为:
1.初始化时将起点s到各个顶点v的距离dist(s->v)赋值为INF,dist(s->s)赋值为0
2.后续进行最多n-1次遍历操作,对所有的边进行松弛操作,假设:
所谓的松弛,以边ab为例,若dist(a)代表起点s到达a点所需要花费的总数,dist(b)代表起点s到达b点所需要花费的总数,weight(ab)代表边ab的权重,
若存在:三角不等式:
(dist(a) +weight(ab)) < dist(b)则说明存在到b的更短的路径,s->...->a->b,更新b点的总花费为(dist(a) +weight(ab)),父节点为a
3.遍历都结束后,若再进行一次遍历,还能得到s到某些节点更短的路径的话,则说明存在负环路
思路上与狄克斯特拉算法(Dijkstra algorithm)最大的不同是每次都是从源点s重新出发进行”松弛”更新操作,而Dijkstra则是从源点出发向外扩逐个处理相邻的节点,不会去重复处理节点,这边也可以看出Dijkstra效率相对更高点。
我们举一个例子:
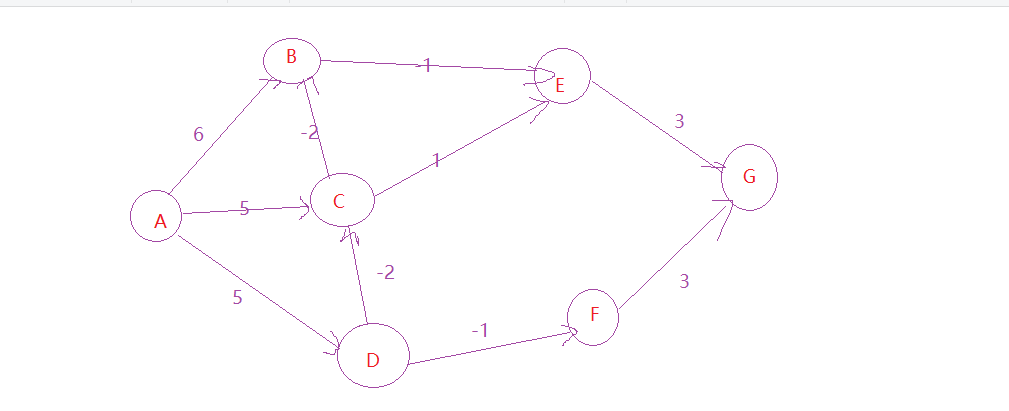
求A到任意一点的距离:
该图共有节点7个,最多需要进行7-1=6次的对所有边的松弛操作
1.进行第一次遍历松弛操作,可以得到:
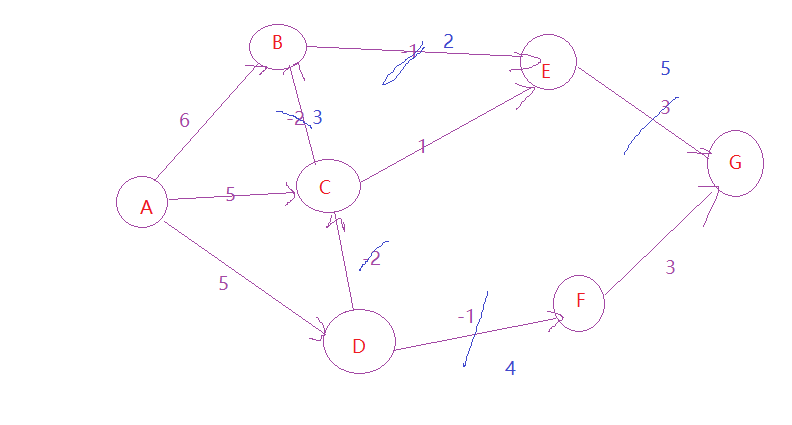
2.进行第二次遍历松弛操作,得到:
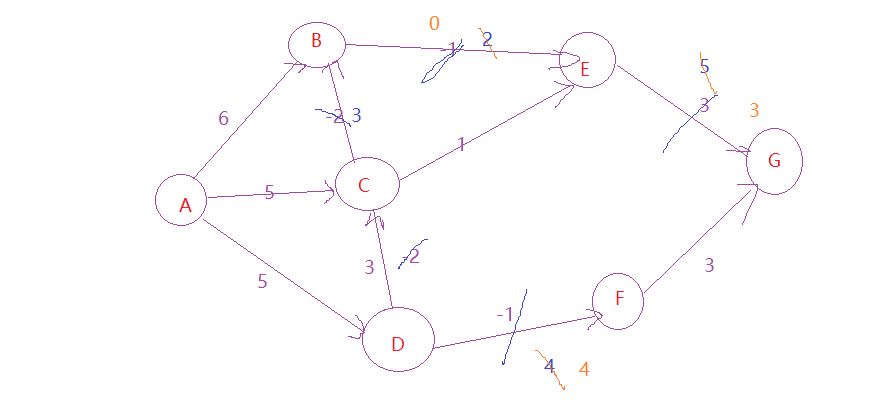
3.再松弛:
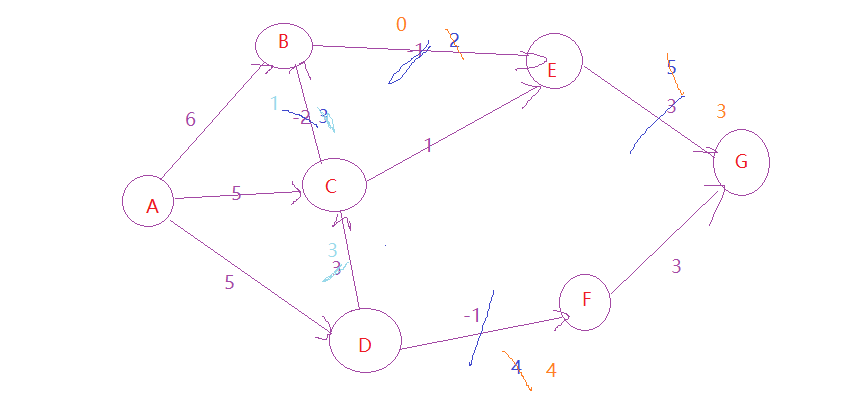
4.此时上表边上A到各个节点的最短路径,可以通过倒序的方式得出路线,只是读入时可能会影响最优路径的顺序
比如上述,AB:6 ,AC:5,AD:5,CB:-2,DC:-2,BE:-1,CE:1,DF:-1,EG:3,FG:3 代码需要遍历3次才可以确认结果(最后一次用于确认结果不再更新);
AB:6,AC:5,AD:5,DC:-2,CB:-2,BE:-1,CE:1,DF:-1,EG:3,FG:3 代码需要遍历2次就可以确认结果;
AB:6,AC:5,AD:5,BE:-1,CE:1,DF:-1,DC:-2,CB:-2,EG:3,FG:3 代码需要遍历4次就可以确认结果;
有时候图的关系是用户输入的,对于顺序并不好强制一定是最佳的!
例题
题意:
就是让我们求从1号点到n号点的最多经过k条边的最短距离!
代码:
struct Edge{
int a,b,c;
}edges[M];
int bellman_ford(){
//初始化
memset(dist,0x3f,sizeof dist);
//定义起点
dist[1]=0;
for(int i=0;i<k;i++){
//把dist复制到backup经行遍历松弛,不会产生串联
memcpy(backup,dist, sizeof dist);
for(int j=0;j<m;j++){
int a=edges[j].a,b=edges[j].b,c=edges[j].c;
//(dist(a) +weight(ab)) < dist(b)则说明存在到b的更短的路径,取最小值
dist[b]=min(dist[b],backup[a]+c);
}
}
if(dist[n]>0x3f3f3f3f/2)return -1;
return dist[n];
}
1.BFS主要适用于无权重向图重搜索出源点到终点的步骤最少的路径,当方向图存在权重时,不再适用
2.Dijkstra主要用于有权重的方向图中搜索出最短路径,但不适合于有负权重的情况.对于环图,个人感觉和BFS一样,标志好已处理的节点避免进入死循环,可以支持
3.Bellman–Ford主要用于存在负权重的方向图中(没有负权重也可以用,但是效率比Dijkstra低很多),搜索出源点到各个节点的最短路径
4.Bellman–Ford可以判断出图是否存在负环路,但存在负环路的情况下不支持计算出各个节点的最短路径。只需要在结束(节点数目-1)次遍历后,再执行一次遍历,若还可以更新数据则说明存在负环路,当人为限制了遍历次数后,对于负环路也可以计算出,但似乎没有什么实际意义
Spfa
前面两个算法,已经可以出单源到任意一个点的距离,而对于负环的判断和时间复杂度Bellman–Ford并没有那么完美:
下面我们看一下用Bellman–Ford队列优化的spfa算法:
算法的思路:
我们用数组dis记录每个结点的最短路径估计值,用邻接表或邻接矩阵来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止,所以他的时间复杂度就是O(m),最坏O(n*m)!
我们要知道带有负环的图是没有最短路径的,所以我们在执行算法的时候,要判断图是否带有负环,方法有两种:
1.开始算法前,调用拓扑排序进行判断(一般不采用,浪费时间)
2.如果某个点进入队列的次数超过N次则存在负环(N为图的顶点数)
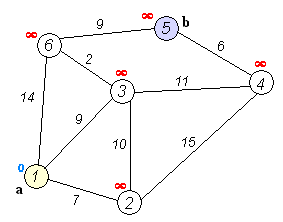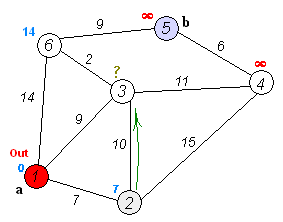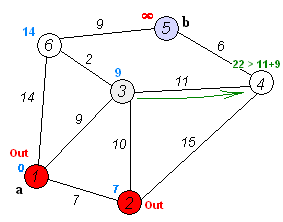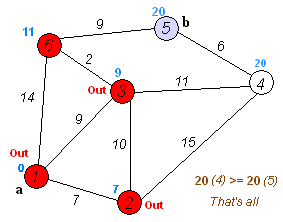
举一个例子:
v首先我们先初始化数组dis如下图所示:(除了起点赋值为0外,其他顶点的对应的dis的值都赋予无穷大,这样有利于后续的松弛)
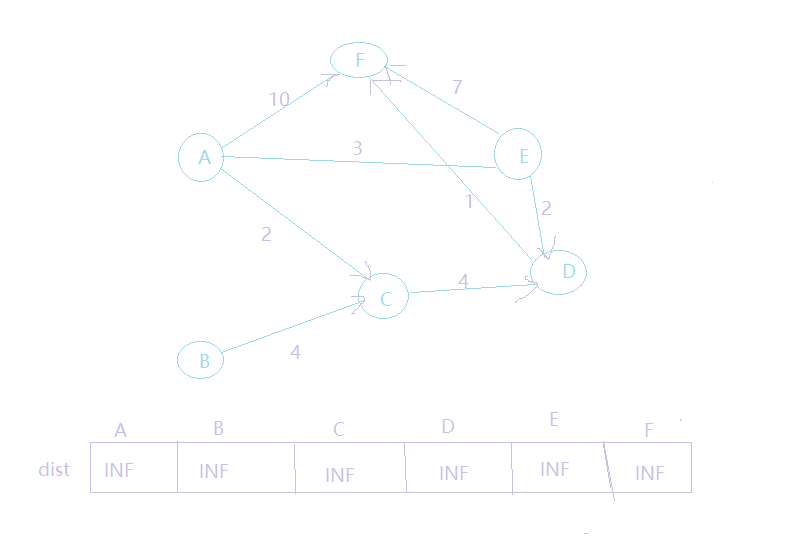
此时,我们还要把a推入队列:{a}现在进入循环,直到队列为空才退出循环。
1.首先,队首元素出队列,即是a出队列,然后,对以a为弧尾的边对应的弧头顶点进行松弛操作,可以发现a到c,e,f三个顶点的最短路径变短了,更新dis数组的值,得到如下结果:
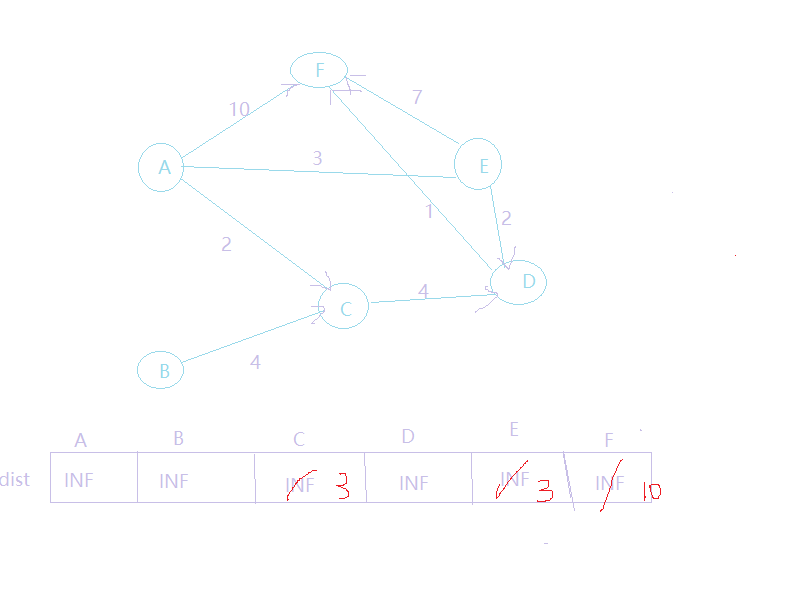
2.我们发现c,e,f都被松弛了,而且不在队列中,所以要他们都加入到队列中:{c,e,f}此时,队首元素为c,c出队列,然后,对以c为弧尾的边对应的弧头顶点进行松弛操作,可以发现a到d的边,经过c松弛变短了,所以更新dis数组,得到如下结果:
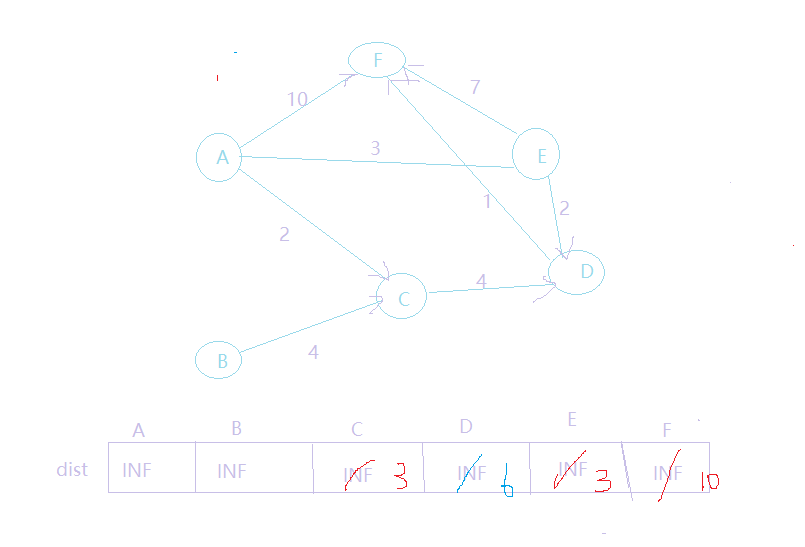
3.此时只有d对应的值被更新了,而且d不在队列中,则把它加入到队列中:{e,f,d}
此时,队首元素为e,e出队列,然后,对以e为弧尾的边对应的弧头顶点进行松弛操作,发现a到d和f的最短路径,经过e的松弛都变短了,更新dis的数组,得到如下结果
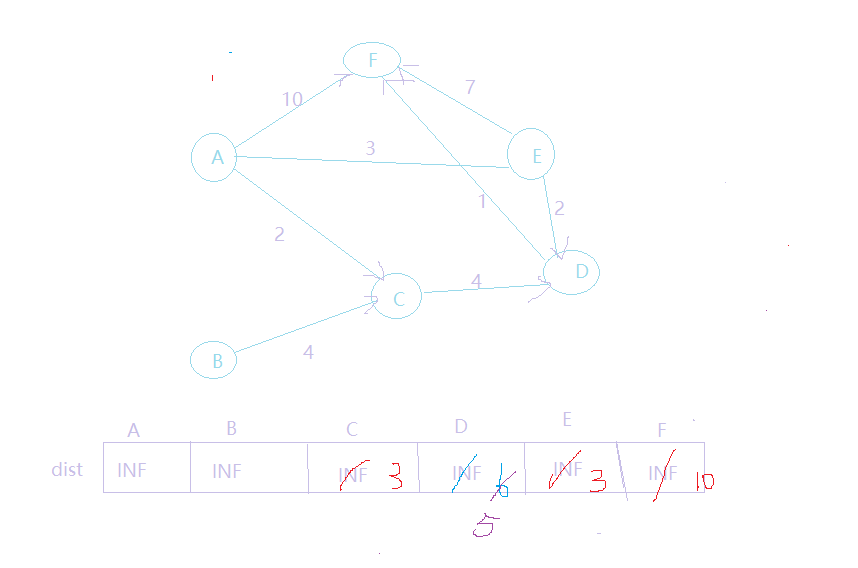
4.我们发现d、f对应的值都被更新了,但是他们都在队列中了,所以不用对队列做任何操作。队列值为:{f,d}
队首元素为f,f出队列,然后,对以f为弧尾的边对应的弧头顶点进行松弛操作,发现f出度为0,所以不变,下面对d处理: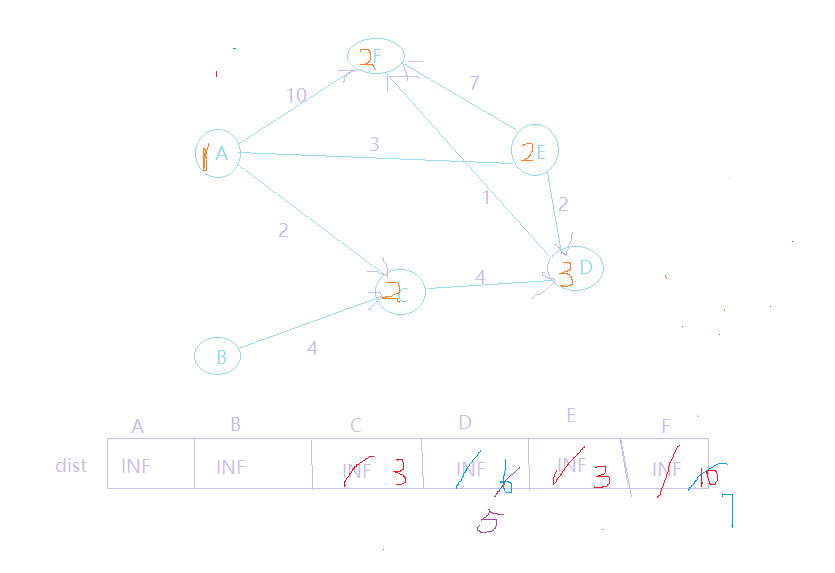
队列元素为,循环停止!得到答案:
习题
由于思路与BFS差不了多少所以直接看代码:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int,int >PII;
const int N=100010;
int h[N],e[N],ne[N],w[N],dist[N],n,m,idx;
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin>>n>>m;
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
int t=spfa();
if(t==0x3f3f3f3f)cout<<"impossible"<<endl;
else cout<<t<<endl;
return 0;
}
Floyd
由于他是一个经典的DP问题,所以我们后面DP部分会详细介绍:
当你想寻找理解我给你一些思路:
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设dist(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查dist(i,k) + dist(k,j) < dist(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置dist(i,j) = dist(i,k) + dist(k,j),这样一来,当我们遍历完所有节点k,dist(i,j)中记录的便是i到j的最短路径的距离。
模板:
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
当然我们由模板就以看出时间复杂度为O(n^3);
模板描述:
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v的距离k 比己知的路径更短。如果是更新它。
习题
这个问题主要看DP状态方程!
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=10010,INF=1e9;
int n,m,k;
int d[N][N];
void floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j)d[i][j]=0;
else d[i][j]=INF;
}
}
while(m--){
int a,b,w;
cin>>a>>b>>w;
d[a][b]=min(d[a][b],w);
}
floyd();
while(k--){
int a,b;
cin>>a>>b;
if(d[a][b]>=INF/2)cout<<"impossible"<<endl;
else cout<<d[a][b]<<endl;
}
return 0;
}
小结
对于图论里面最短路算法,无负权基本上用堆优化Dijkstra,效率是比较乐观的,而且他还有优先队列优化!对于bellman-ford,像是Dijkstra到Spfa的一个过渡!
Spfa算法的基本思路与贝尔曼-福特算法相同,即每个节点都被用作用于松弛其相邻节点的备选节点,spfa算法的提升在于它并不盲目尝试所有节点,而是维护一个备选节点队列,并且仅有节点被松弛后才会放入队列中。整个流程不断重复直至没有节点可以被松弛。当然这里我最喜欢Floyd,就时间复杂度不尽如人意!
对于最短路算法的看法就是这些了,当然由于图论的一些思想不好接受,慢慢理解,谢谢你能把它阅读完!希望你有所收获!
yxc老师的模板 链接
朴素dijkstra算法 —— 模板题 AcWing 849. Dijkstra求最短路 I
时间复杂是 O(n2+m)O(n2+m), nn 表示点数,mm 表示边数
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
堆优化版dijkstra —— 模板题 AcWing 850. Dijkstra求最短路 II
时间复杂度 O(mlogn)O(mlogn), nn 表示点数,mm 表示边数
typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
Bellman-Ford算法 —— 模板题 AcWing 853. 有边数限制的最短路
时间复杂度 O(nm)O(nm), nn 表示点数,mm 表示边数
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在负权回路。
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
spfa 算法(队列优化的Bellman-Ford算法) —— 模板题 AcWing 851. spfa求最短路
时间复杂度 平均情况下 O(m)O(m),最坏情况下
O(nm)O(nm), nn 表示点数,mm 表示边数
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
spfa判断图中是否存在负环 —— 模板题 AcWing 852. spfa判断负环
时间复杂度是 O(nm)O(nm), nn 表示点数,mm 表示边数
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N], cnt[N]; // dist[x]存储1号点到x的最短距离,cnt[x]存储1到x的最短路中经过的点数
bool st[N]; // 存储每个点是否在队列中
// 如果存在负环,则返回true,否则返回false。
bool spfa()
{
// 不需要初始化dist数组
// 原理:如果某条最短路径上有n个点(除了自己),那么加上自己之后一共有n+1个点,由抽屉原理一定有两个点相同,所以存在环。
queue<int> q;
for (int i = 1; i <= n; i ++ )
{
q.push(i);
st[i] = true;
}
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true; // 如果从1号点到x的最短路中包含至少n个点(不包括自己),则说明存在环
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
floyd算法 —— 模板题 AcWing 854. Floyd求最短路
时间复杂度是 O(n3)O(n3), nn 表示点数
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
作者:yxc
链接:https://www.acwing.com/blog/content/405/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。


求问BFS求最短路会遇到什么问题
%%%%%%%%%%%%%%%%
%%
朋友 写的很棒,dijkstra的堆优化那里,在if(st[ver])continue; 之后的某个地方是不是要设置 st[ver] =true;
这个不需要!hhh
写得很好,必须赞一个!
我感觉我分析的堆优化dikjstra时间复杂度是o(n+mlog(m)),n代表边数,m是点数,有一点问题!hhh
一共有 n 条边的话,那么下面的代码最多就会执行 n 次:
if (dist[j] > distance + w[i]) { dist[j] = distance + w[i]; heap.push({dist[j], j}); }因此最多会向堆中插入 n 次,所以时间复杂度是 O(nlogn)~
理解了,我考虑的太多了,hh
如果 n 表示边数,m 表示点数的话,dijkstra算法的时间复杂度是可以优化到 O(n+mlogm) 的,不过要是用菲波那切堆hh,但这个数据结构只具有理论价值,虽然理论时间复杂度低,但常数巨大,不适用哈哈
恍然大悟,以前就一直认为它用小根堆可以优化到O(n+mlogm)hh,搞混了。
给大佬提个小建议,像这种比较好的分享帖,是不是可以采取一些激励措施,比如每周评选最好的几个分享帖给一些小奖励。还有很多同学的题解或者分享只有代码没有解释甚至注释都没有,等以后用户量大了之后是否可以添加一些审核。
收到!以后可以评选一些每周之星之类的,给一些头衔
请问堆优化版本的Dijkstra算法是使用小顶堆优化内层第一个循环,邻接表来优化内层第二个松弛循环吗?
对滴
很棒啊!
感觉写的太繁琐了,下一次再发一个精简的!晚上,加油,秦同学!
今天晚上y总有课,我明天晚上。hh
明天晚上我好像要开始夏令营了!!!不过应该可以看你直播!
加油哦!