论执着与稳重的好处----DFS/BFS

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

论执着与稳重的好处----DFS/BFS

作者：

wuog , 2019-08-11 01:46:34 , 所有人可见 , 阅读 4368

87

134

DFS与BFS

定义一个小小的目标：

1.DFS?
2.BFS?
3.DFS与BFS的运用（指代码实现）！

首先我们来简单看一下这两个算法：

稳重的BFS：
一般情况下我们是用队列来实现，先进先出，使用队列保存未被检测的结点。结点按照宽度优先的次序被访问和进出队列。思路大概是这样：

  1.先初始化队列q；
  2.从起点开始访问，并且改变他的状态为已经访问；
  3.如果他的队列非空，取出首个元素，将它弹出！
  4.如果u==目标状态，然后对所以与u邻近的点进入队列；
  5.标记它已经被访问！

他的遍历思想是：遍历树的层次！
举一个例子：就像你掉了东西，你的寻找范围就是从你对身边周围一直扩散！

DFS的固执：
一直往深处走，直到找到解或者走不下去为止，使用栈保存未被检测的结点，结点按照深度优先的次序被访问并依次被压入栈中，并以相反的次序出栈进行新的检测。思路：

dfs(int u)
{
    if(找到了||走不下去了)
    {
        return；

    }
    开始下一个情况（dfs(u+1)）;

}

再细分一下：

dfs()//参数用来表示状态  
{  
    if(到达终点状态)  
    {  
        ...//根据题意添加  
        return;  
    }  
    if(越界或者是不合法状态)  
        return;  
    if(特殊状态)//剪枝
        return ;
    for(扩展方式)  
    {  
        if(扩展方式所达到状态合法)  
        {  
            修改操作;//根据题意来添加  
            标记；  
            dfs（）；  
            (还原标记)；  
            //是否还原标记根据题意  
            //如果加上（还原标记）就是 回溯法  
        }  

    }  
}

他的搜索思路是：
就像你去学习一个混合运算，你要必须学习加法思想，然后减法，再是乘除（不要当杠精，好好理解，哈哈哈）！

BFS

我们现在了解了一些基本的知识点，我们来看一下他们具体是怎么样去具体运作与实现！

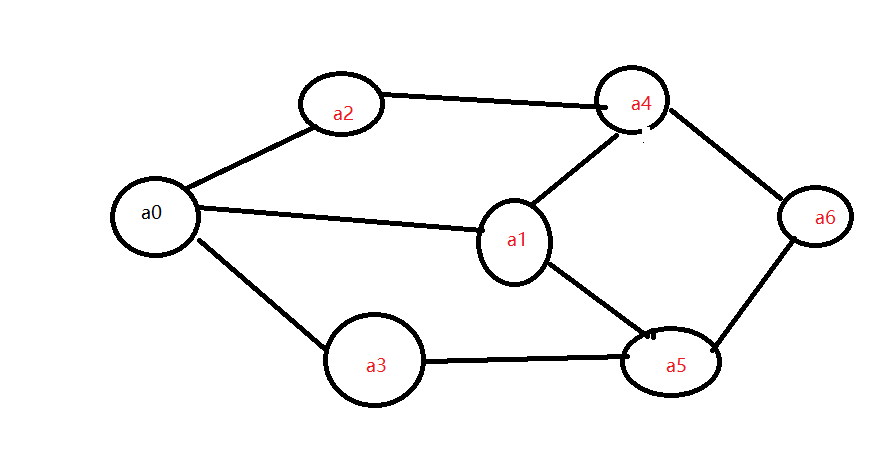
捕获.PNG
广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。如图所示，要想遍历从a0到a6的每一个顶点，我们可以设a0为第一层，a1、a2、a3为第二层，a4、a5为第三层，a6为第四层，再逐个遍历每一层的每个顶点。
具体过程如下：
1.准备工作：创建一个bool str[]数组，用来记录已被访问过的顶点；创建一个队列，用来存放每一层的顶点；初始化图g。
2.从图中的a0开始访问，将的st[a0]数组的值设置为true，同时将a0入队。
3.只要队列不空，则重复如下操作：
(1)队头顶点u出队。
(2)依次检查u的所有邻接顶点w，若st[w]的值为false，则访问w，并将st[w]置为true，同时将w入队。

文字理解过于复杂我们看一下图：

1.初始状态：

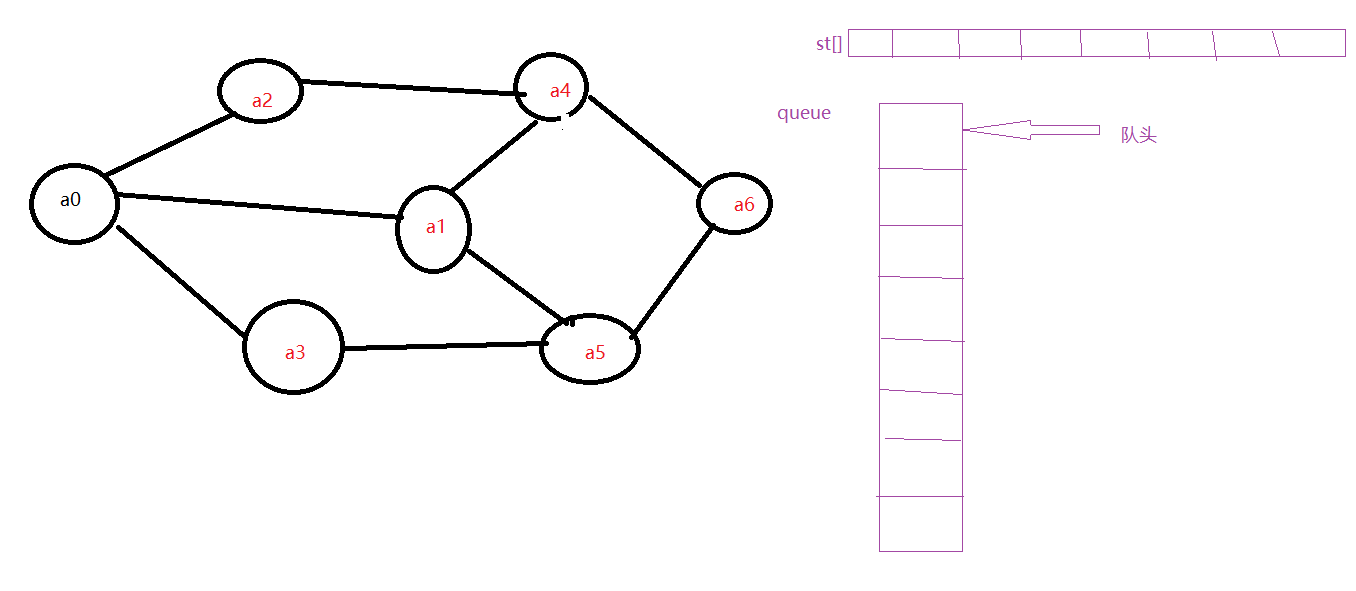
2.开始访问顶点a0，并改变st[0]的值为T，同时将a0入队。：

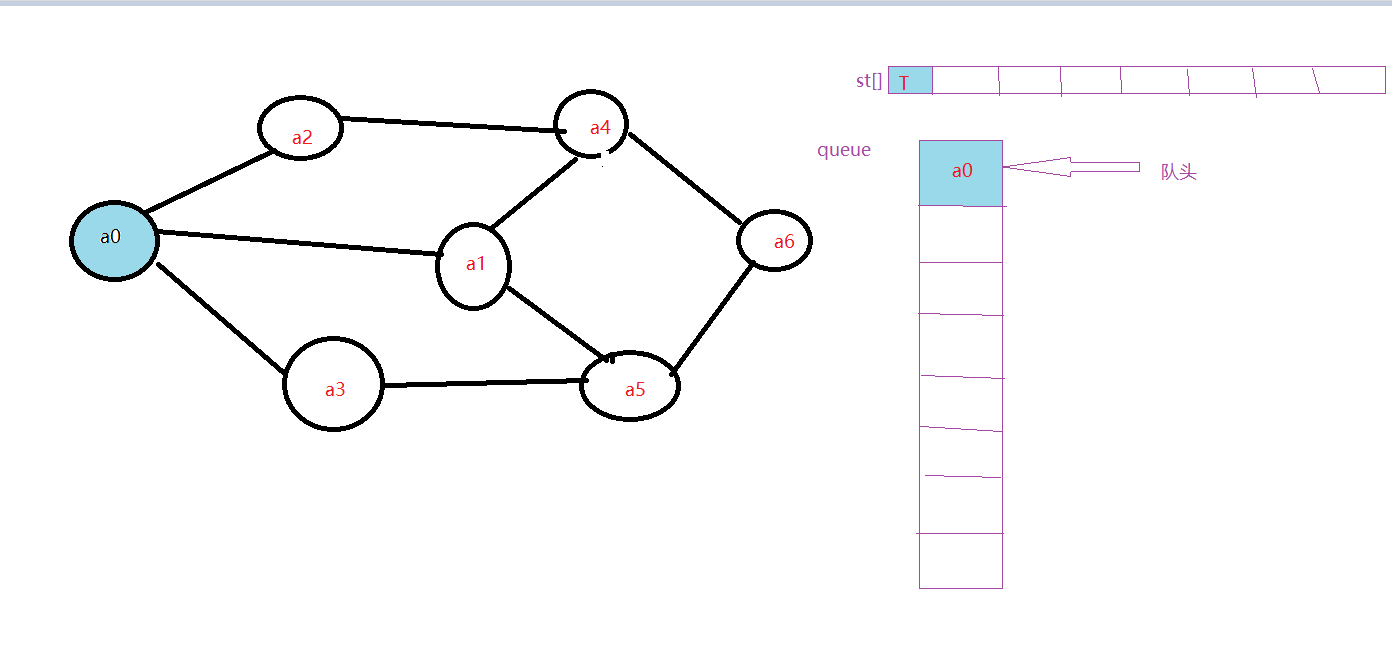
3.将a0出队，开始访问第二层，访问a0的邻接点a1。判断st[1]，因为st[1]的值为F，访问a1

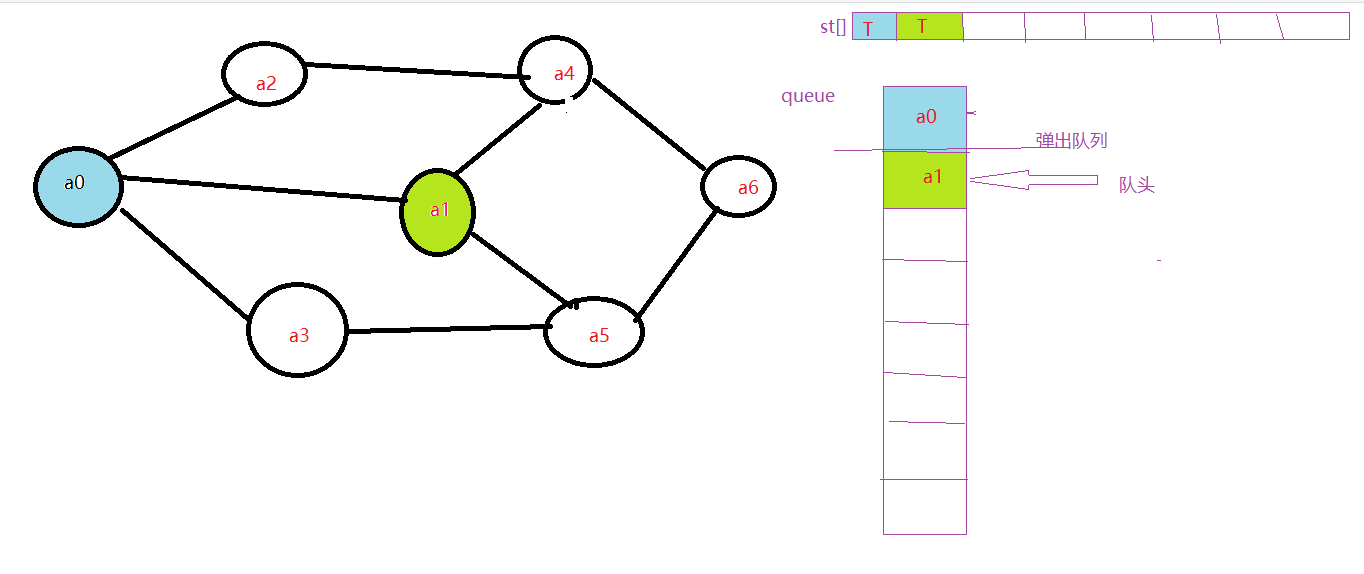
4.访问a0的第二个邻近元素a2,因为st[2]为F,访问a2

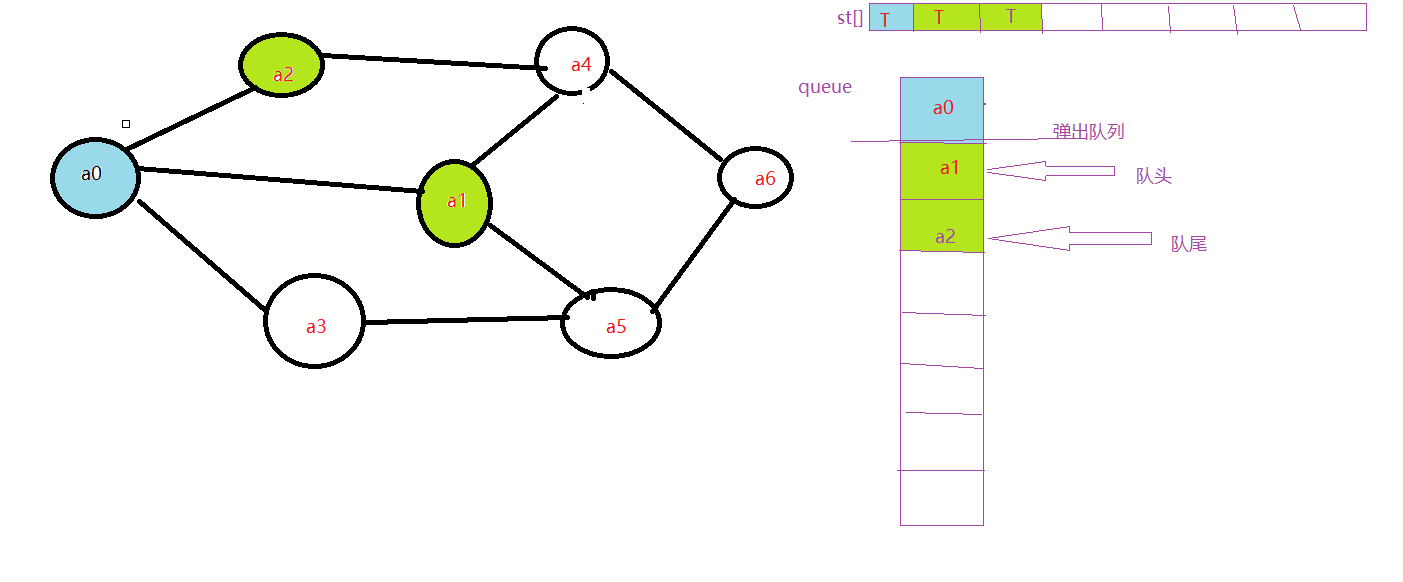
5.开始访问第三个元素，因为st[3]为F,所以可以访问a3

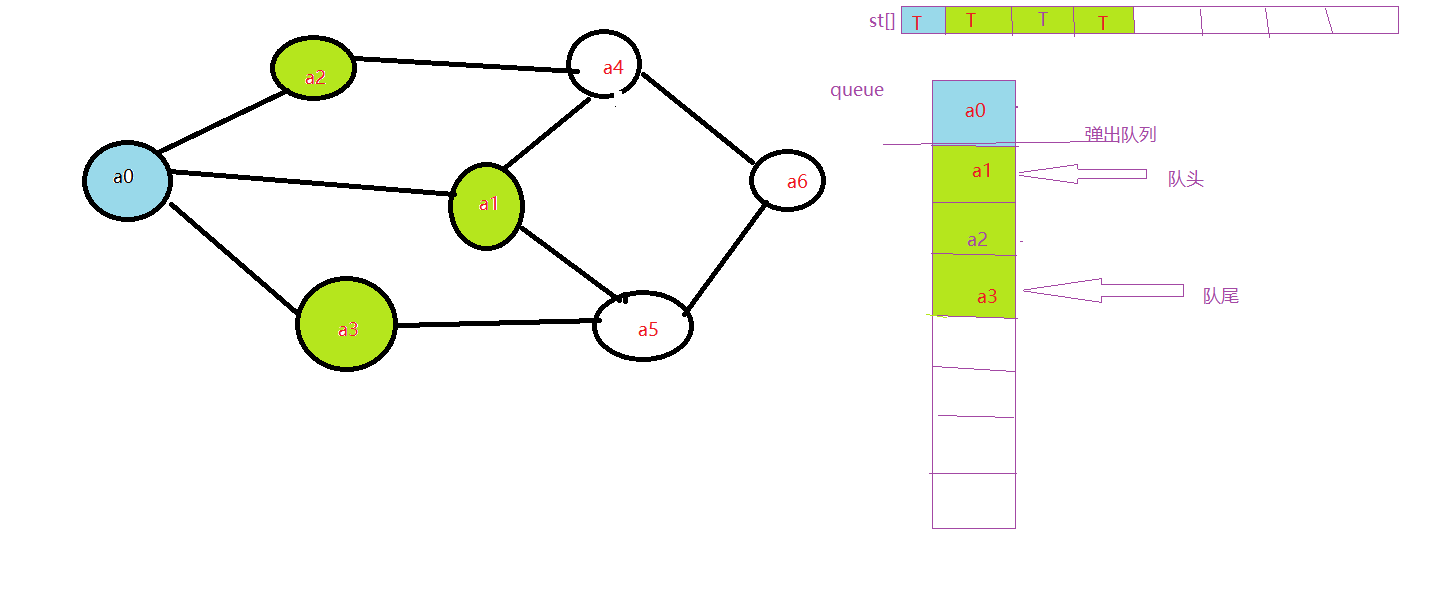
6.a0的全部邻接点均已被访问完毕。将队头元素a1出队，开始访问a1的所有邻接点。开始访问a1邻接点a0，判断st[0]，因为其值为T，不进行访问。继续访问a1邻接点a4，判断st[4]，因为其值为F，访问a4

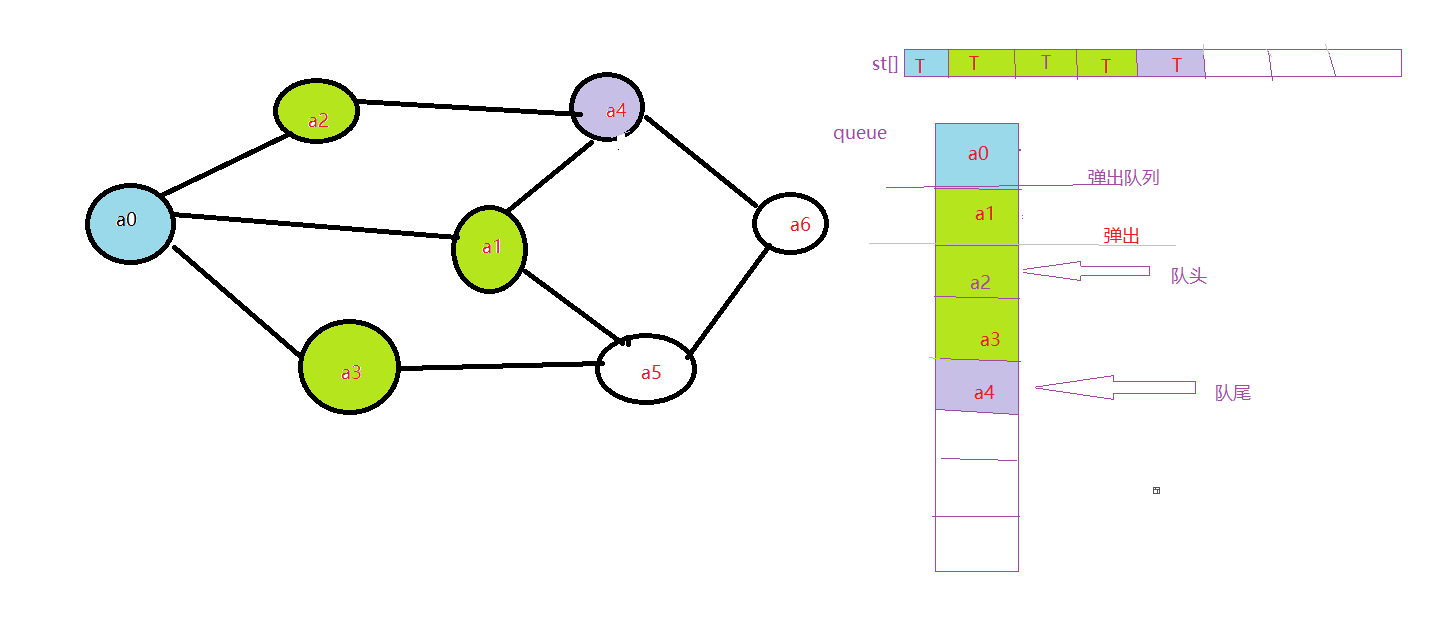
7.开始访a5,因为st[5]为F,访问a5

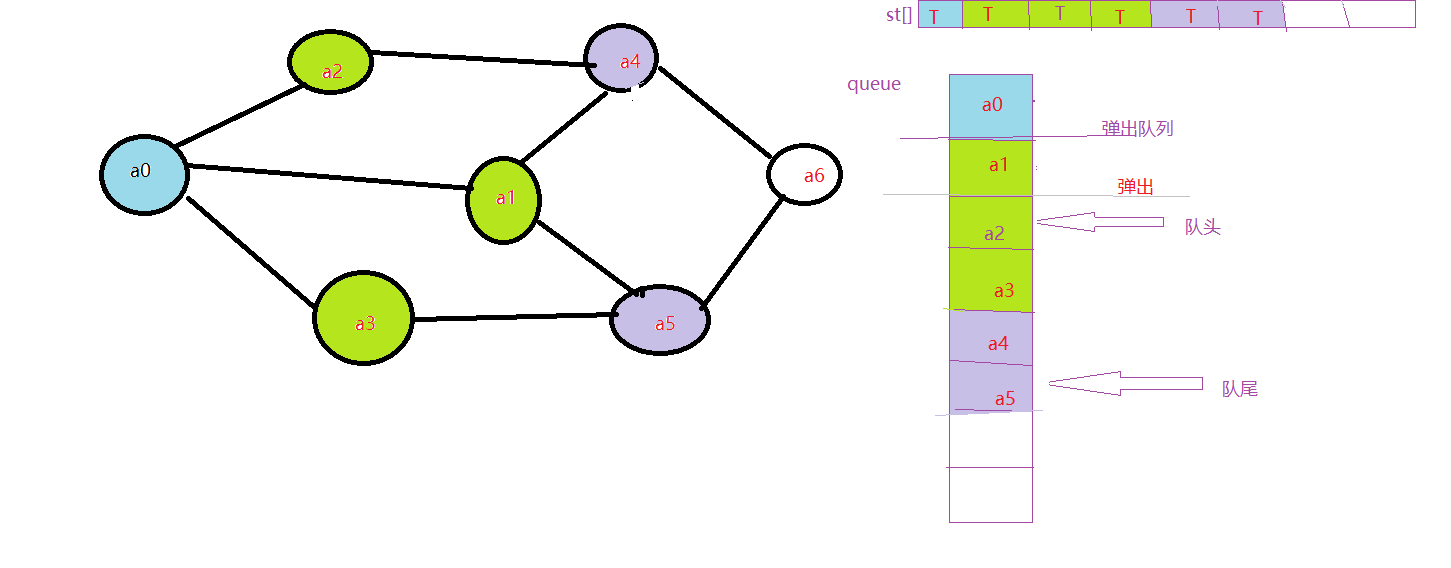
8.由于a4的邻近值a1,a2都变为了T，所以就不再访问，直接弹出队列：

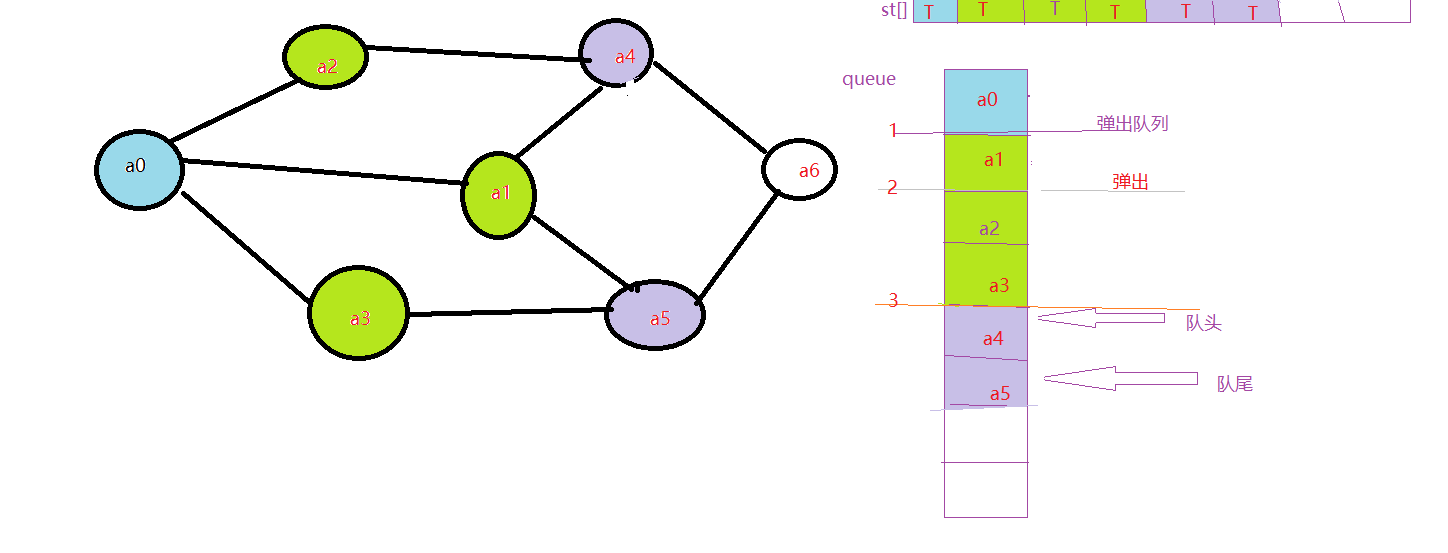
9.开始访问a4的邻近元素，因为a1,a2的状态为T,a6的st[6]为F,所以访问a6,a4弹出队列

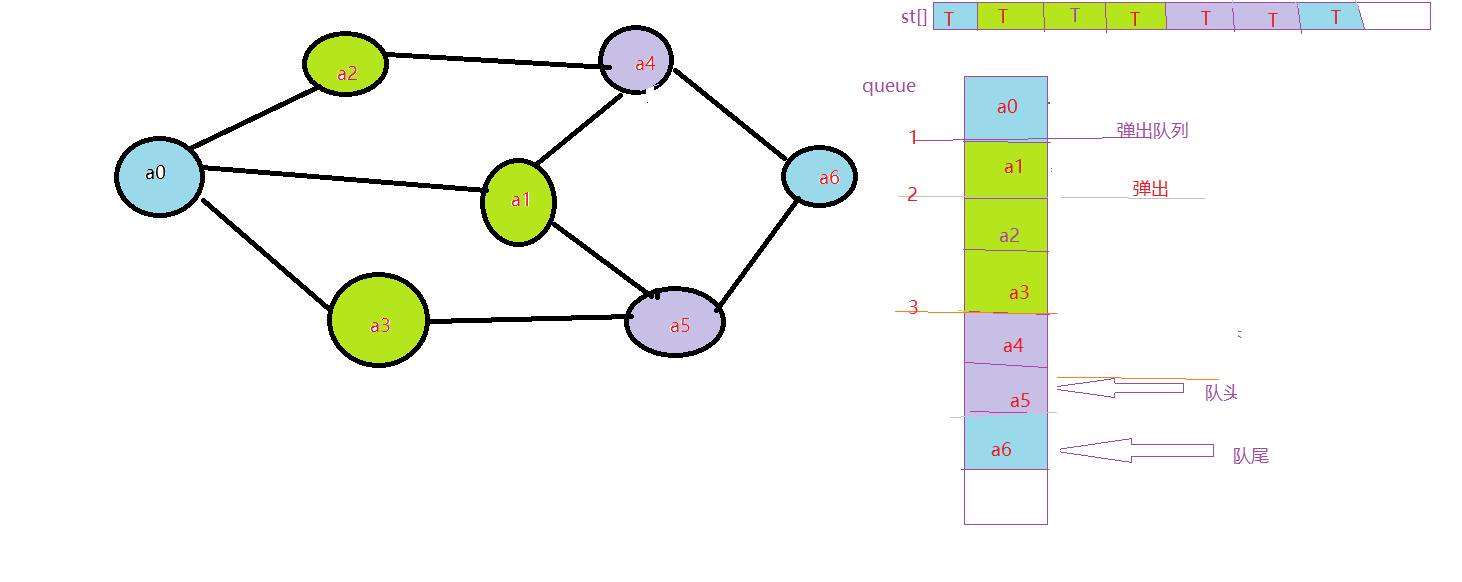
10.由于a5邻近值都为T，所以直接弹出！

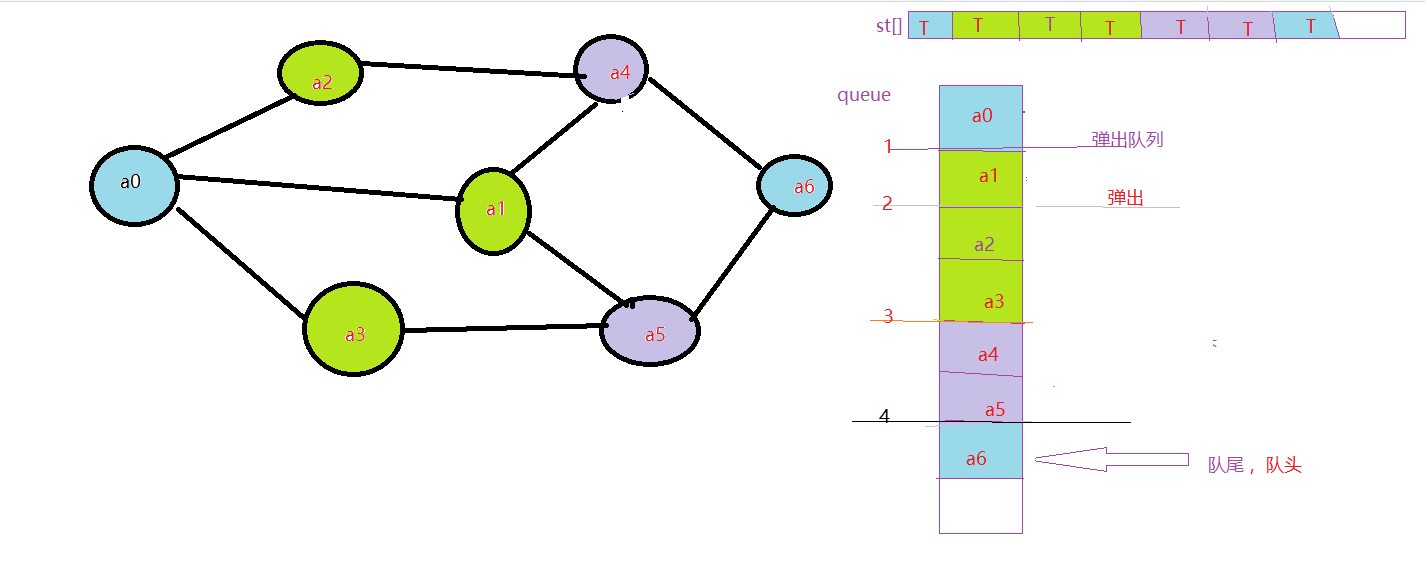
11.然后访问a6,但是由于邻近元素全无T,所以弹出a6

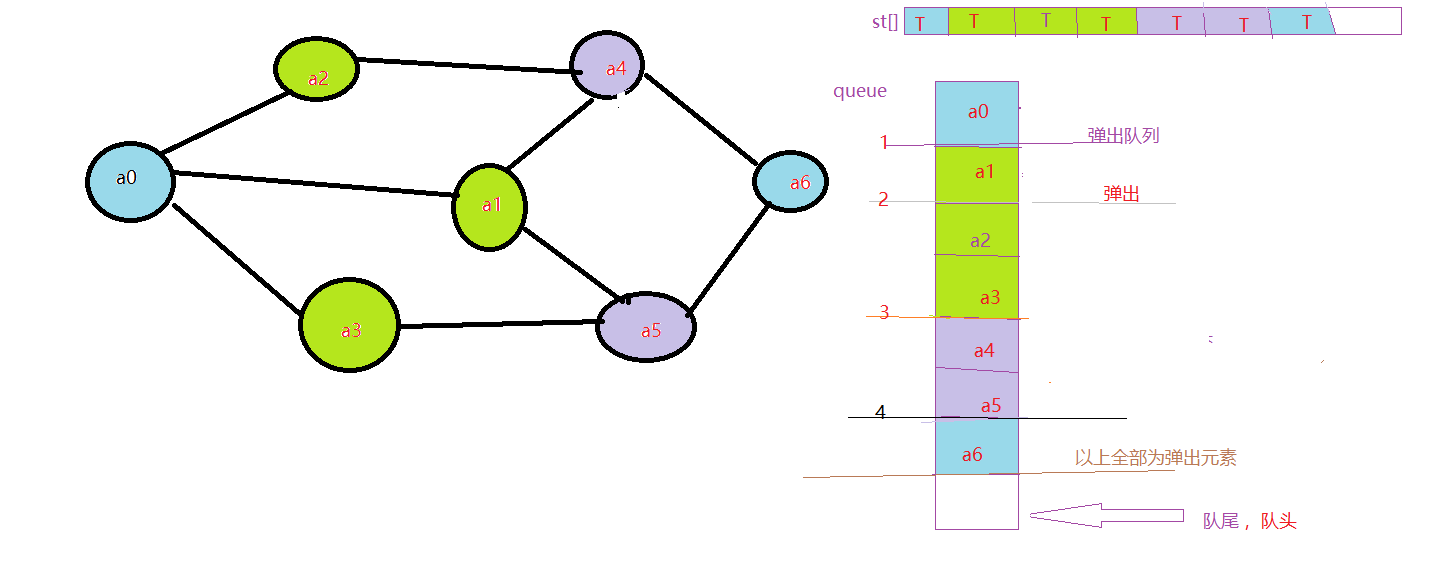
好了这就是BFS,搜索的全过程，你可以试着去分析代码：
我们来看一下代码去实现：

queue<int> q;
st[0] = true; // 表示1号点已经被遍历过
q.push(0);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!s[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

习题

习题链接
题意：
就是bfs最拿手的问题————最优解：
模拟队列代码：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int ,int > PLL;
const int N=110;
int n,m;
int g[N][N],d[N][N];
PLL q[N*N];
int bfs()
{
    int hh=0,tt=0;

    q[0]={0,0};//先初始化
    memset(d,-1,sizeof d);//状态值
    d[0][0]=0;//开始访问
   int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};//邻近元素坐标变换

   while(hh<=tt){

       auto t=q[hh++];//开始搜索
       for(int i=0;i<4;i++)
       {
       int x=t.first+dx[i],y=t.second+dy[i];//邻近元素的访问
       if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1)//未访问
       {
           d[x][y]=d[t.first][t.second]+1;//改变状态
           q[++tt]={x,y};//推入邻近未访问元素
       }

       }
   }
   return d[n-1][m-1];
}
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++)
      for(int j=0;j<m;j++)
          cin>>g[i][j];

    cout<<bfs()<<endl;

    return 0;


}

我们在看一个图：

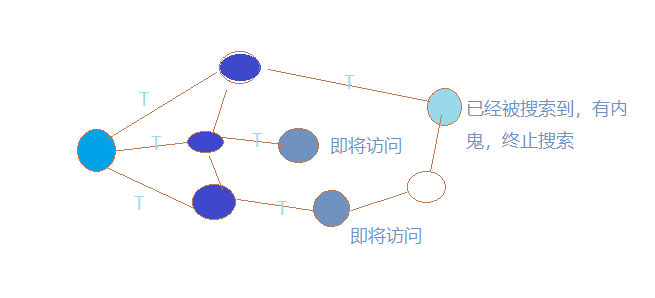
DFS

有了BFS的基础我们更加简单去理解DFS:

准备工作：创建一个bool st[]数组，用于记录所有被访问过的顶点。

1.从图中a0出发，访问a0。

2.找出a0的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。

3.返回前一个访问过的仍有未被访问邻接点的顶点，继续访问该顶点的下一个未被访问领接点。

4.重复2,3步骤，直至所有顶点均被访问，搜索结束。

下面我们将以图的形式展示：

为了不必要的文字叙述：
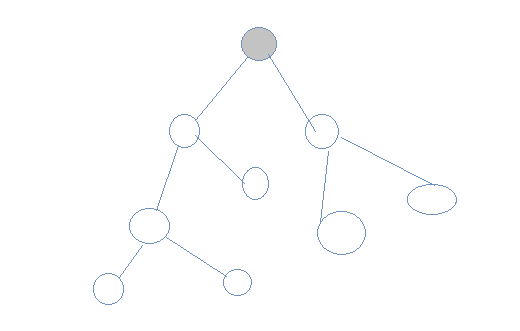
我们规定白色表示未被访问，灰色表示即将访问，红色色表示已访问：
1.开始访问

2.向下，改变st状态

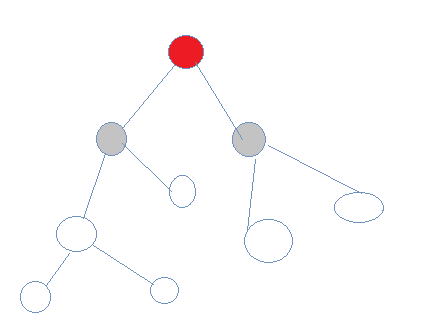
3.向下，改变st状态

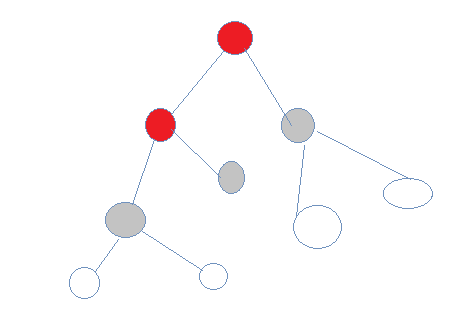
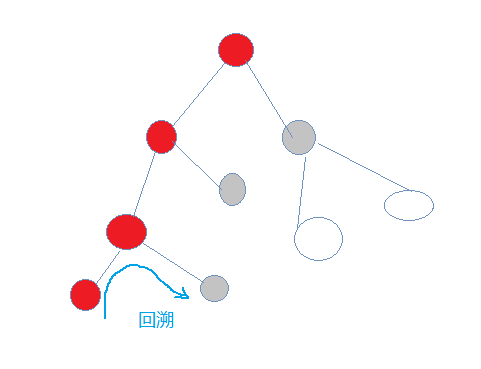
4.向下，改变st状态

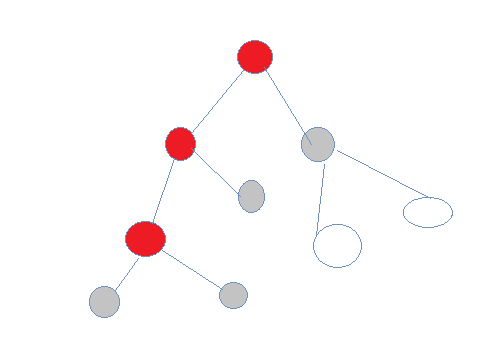
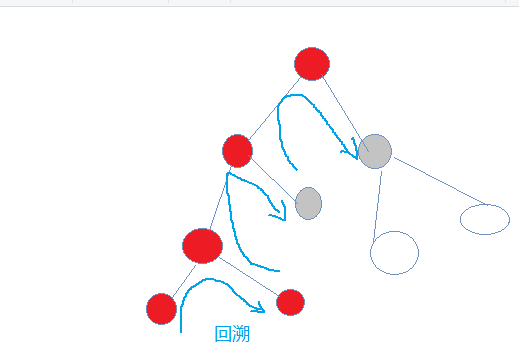
5.有for循环和st状态解决这个回溯问题

6.

7.由于内容具有极大的相似性，所以后面过程类似！！

习题

习题链接
代码：

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])//循环与st完成了回溯
    {
        int j = e[i];
        if (!st[j]) 
        dfs(j);//向下
    }
}

题意：
就是DFS再加上了一些限定条件和搜索目标：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=200010;

int ne[N],e[N],idx,h[N];
bool  st[N];
int n,ans=N;

void add(int a,int b){
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}

int dfs(int u){
    st[u]=true;

    int sum=0,size=0;

    for(int i=h[u];i!=-1;i=ne[i]){

        int j=e[i];

        if(st[j])continue;

        int s=dfs(j);
        size=max(size,s);
        sum+=s;

    }
    size=max(size,n-sum-1);
    ans=min(ans,size);
    return sum+1;
}


int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    cin>>n;

    memset(h,-1,sizeof h);
    int t=n-1;
    while(t--){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);

    }
    dfs(1);
    cout<<ans<<endl;
    return 0;

}

小结

当然但看DFS与BFS的理解，是非常简单的，但是一些关于他们的题，都是在他们的基础上进行拓展到！就例如迷宫问题，他就是一个BFS入门，但是它就在你理解的基础上，把st的状态值不全是false,这就说明有一些路是直接可以pop的，先到达就停止！当然你认为这个比较简单，但是我如果给每一条边加上权重，算最优解！我们又该如何思考？宽搜（BFS）与深搜（DFS）,一个侧重全面。一个侧重与效率!由于算法的存储，后续我写一下图的基本概念方便理解！（如：有无环，有无向，连通）好了，这个就是DFS/BFS的知识点！希望你有所所获，感谢你的阅读！

如果你想有所提高，这是法宝 0x20
~~题解会有的~~

yxc的模板链接

树与图的遍历
时间复杂度 O(n+m)O(n+m), nn 表示点数，mm 表示边数
(1) 深度优先遍历 —— 模板题 AcWing 846. 树的重心

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}
(2) 宽度优先遍历 —— 模板题 AcWing 847. 图中点的层次

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!s[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

作者：yxc
链接：https://www.acwing.com/blog/content/405/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。