鄙人不才,此中鄙陋甚多,望海涵!!!
首先简单分析一下题目:给出至多4个每个面都有颜色的正方体,我们可以任意翻转这些正方体且不消耗代价,但有的时候并不是翻转就能让这4个正方体完全一样(same指每个正方体的面颜色相同),我们还可以通过消耗代价的涂色来解决问题(重新涂色一个面消耗一代价),问最终最少消耗多少代价可以实现same!
/-------------------------------------------------------------------------------------------------------------------------------------------------/
看到这个题目我们的第一想法肯定是能旋转解决的肯定不会通过重涂来解决!当然这样的想法肯定没错,接下来我们就要想怎么让他实现旋转呢?
一·规定正方行摆放!
一共四个正方体,并不多,从某种意义上讲我们可以试试暴力枚举所有旋转的情况,接下来的关键就是何不重不漏不乱(注:不乱是非必要条件,但一乱很难做对)的枚举每一种情况,这里刘佬的做法非常精妙,我们将正方体的摆放分为2步!
1.首先是确定顶部的那个面是几(这里以及下面我们的面都定位0,1,2,3,4,5号面)
2.再确定前面的面的编号这样一共可以分为6(顶部那个面的情况)*4(前面的面情况)=24种情况!
二·得到所有旋转的情况!!!(极其重要的一步)
题目给出我们的6个颜色都是对应着的标准正方体的颜色!
即:前 右 顶 底 左 后(附图)
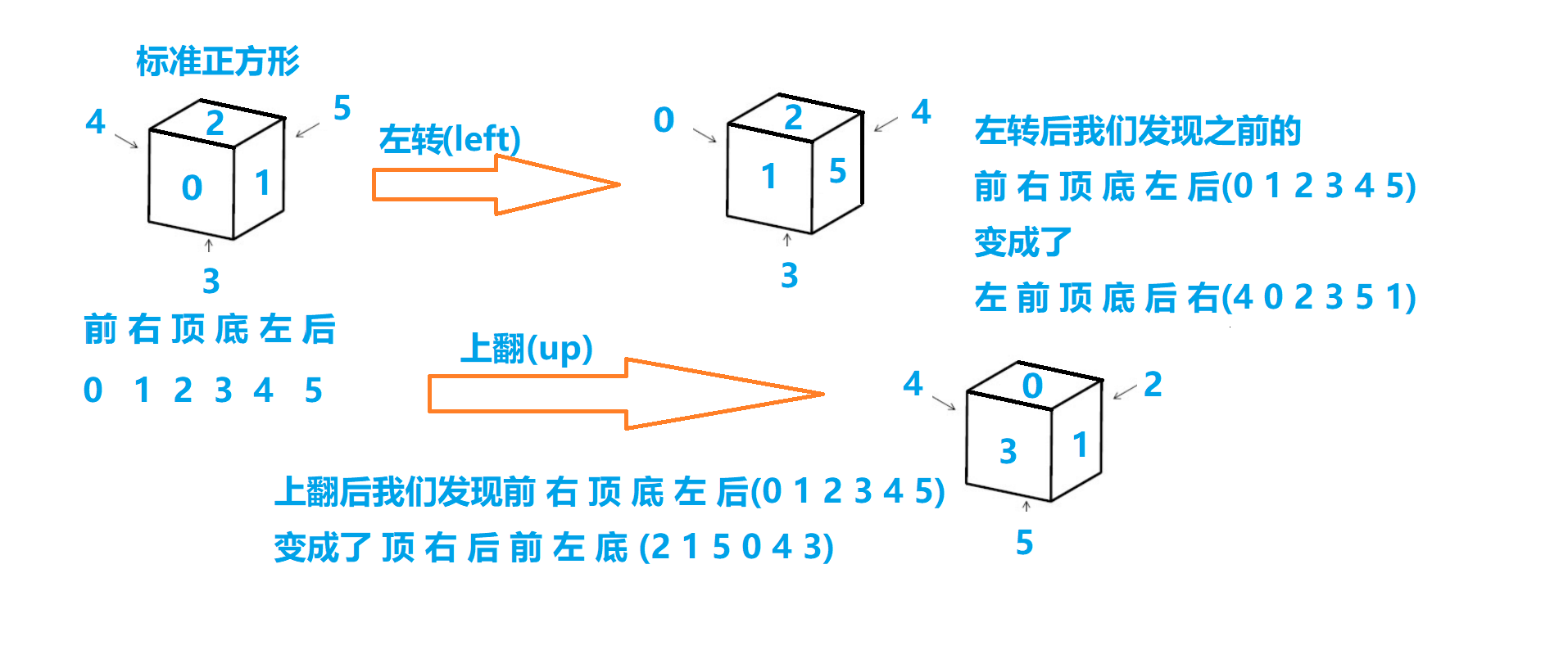
我们再想对于给定正方体我们可以用哪几个精简的操作就能实现所有的情况枚举:有了前面我们正方体摆放的规定,我们应该不难理解分为2步的操作,即左转和上转(附图),所有的操作都可以由这2步组合而成:下面附上从标准变为其他状态的6种操作组合:
* 0在顶面:上翻1,左0~3
* 1在顶面:左1,上1,左0~3
* 2在顶面:左0~3
* 3在顶面:上2,左0~3
* 4在顶面:左3,上1,左0~3
* 5在顶面:左2,上1,左0~3
因此我们只要实现左操作和上操作即可!
附上图解析与数表代码!
数表代码
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
int lef[6]={4,0,2,3,5,1};
int up[6]={2,1,5,0,4,3};
//将p进行t旋转
//这里的指针实现了引用的功能直接对原地址下的p进行修改(即实现转)
void rot(int* t,int* p)
{
int q[6];//q为临时数组,用于存储之前的0,1,2,3,4,5这6个面对应所在的面
memcpy(q,p,sizeof q);
for(int i=0;i<6;i++) p[i]=t[q[i]];
}
void enum_order()
{
int p0[6]={0,1,2,3,4,5};
printf("int dice[24][6] = {\n");
for(int i=0;i<6;i++)
{
int p[6];
memcpy(p,p0,sizeof p0);
//枚举6种情况
//0在顶面:上翻1,左0~3
if(i==0) rot(up,p);
//1在顶面:左1,上1,左0~3
else if(i==1) {rot(lef,p); rot(up,p);}
//2在顶面:左0~3
//3在顶面:上2,左0~3
else if(i==3) {rot(up,p); rot(up,p);}
//4在顶面:左3,上1,左0~3
else if(i==4) {rot(lef,p);rot(lef,p);rot(lef,p); rot(up,p);}
//5在顶面:左2,上1,左0~3
else if(i==5) {rot(lef,p);;rot(lef,p); rot(up,p);}
//枚举所有情况下的左0~3
for(int j=0;j<4;j++)
{
printf("{%d, %d, %d, %d, %d, %d}, \n",p[0],p[1],p[2],p[3],p[4],p[5]);
rot(lef,p);
}
}
printf("};\n");
}
int main()
{
enum_order();
return 0;
}
三.找到一种合适的枚举方法来处理好旋转与重涂的结合!
这里我们让第一个正方体作为标准不动,枚举其余正方体的旋转来不断更新重涂的次数,以达到尽可能的少!(O(24^3)程序可行)下附上代码,我个人认为刘佬处理此题输入的方式太精美了,建议反复阅读!
最终代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=4;
int n,dice[N][6],ans;//dice用来存储颜色编号,后续再详细介绍
int r[N],color[N][6];//r表示每一个正方体的旋转方式
vector<string> names;//color表示每个正方体每个面对应的颜色
int ID(string name)//每一个ID对应着每一种颜色
{
int n=names.size();
for(int i=0;i<n;i++)
if(names[i]==name) return i;
names.push_back(name);
return n;
}
int dice24[24][6] = {{2, 1, 5, 0, 4, 3}, {2, 0, 1, 4, 5, 3},
{2, 4, 0, 5, 1, 3}, {2, 5, 4, 1, 0, 3}, {4, 2, 5, 0, 3, 1},
{5, 2, 1, 4, 3, 0}, {1, 2, 0, 5, 3, 4}, {0, 2, 4, 1, 3, 5},
{0, 1, 2, 3, 4, 5}, {4, 0, 2, 3, 5, 1}, {5, 4, 2, 3, 1, 0},
{1, 5, 2, 3, 0, 4}, {5, 1, 3, 2, 4, 0}, {1, 0, 3, 2, 5, 4},
{0, 4, 3, 2, 1, 5}, {4, 5, 3, 2, 0, 1}, {1, 3, 5, 0, 2, 4},
{0, 3, 1, 4, 2, 5}, {4, 3, 0, 5, 2, 1}, {5, 3, 4, 1, 2, 0},
{3, 4, 5, 0, 1, 2}, {3, 5, 1, 4, 0, 2}, {3, 1, 0, 5, 4, 2},
{3, 0, 4, 1, 5, 2}, };
void check()
{
for(int i=0;i<n;i++)
for(int j=0;j<6;j++)
//让每个旋转后的面对应旋转前的颜色
color[i][dice24[r[i]][j]]=dice[i][j];
//上面这句话包含的一个隐藏信息,虽说我们强调第一个不旋转,但实际比
//较时第一个的初态却是已经是经过一次向上翻转后的状态,我们所谓的不
//旋转只是说不去枚举他旋转的情况罢了!不增加时间复杂度
int tot=0;
for(int i=0;i<6;i++)//枚举6个面
{
int cnt[N*6];//记录当前的面在每个正方体中的颜色出现次数
memset(cnt,0,sizeof cnt);
int maxv=0;//记录最大重复颜色
for(int j=0;j<n;j++) maxv=max(maxv,++cnt[color[j][i]]);
tot+=n-maxv;
}
ans=min(ans,tot);
}
void dfs(int u)
{
if(u==n)
{
check();
return;
}
for(int i=0;i<24;i++)
{
r[u]=i;
dfs(u+1);
}
}
int main()
{
while(cin>>n,n)
{
names.clear();
for(int i=0;i<n;i++)
for(int j=0;j<6;j++)
{
char name[30];
scanf("%s",name);
dice[i][j]=ID(name);
}
ans=n*6;//上界
r[0]=0;//第一个不旋转
dfs(1);
printf("%d\n",ans);
}
return 0;
}


蒟蒻