1. 01 背包问题

0/1 背包问题是实际当中经常遇到的一类经典 NP－hard 组合优化问题之一

2. 动态规划

动态规划方法建立在最优原则的基础上， 可以很好地解决许多用贪心方法无法解决的 问题。和贪心方法一样， 在动态规划中， 可将一个问题的解决方案视为一系列决策的结果。 不同的是， 在贪心方法中， 每采用一次贪心准则便做出一个不可撤回的决策， 而在动态 规划中， 还要考察每个最优决策序列中是否包含一个最优子序列。即要求：无论过程的初 始状态和初始决策是什么，其余的决策必须相对于初始决策所产生的状态构成一个最优决策序列

3. 背包问题

3.1 背包问题的提出

​ 给定 n 种物品和 1 个背包。物品 i 的重量是 wi，其价值为 vi，背包的容量为 C。问应如 何装入背包中的物品，使得装入背包中物品的总价值最大？ 在选择装入背包的物品时，对每种物品 i 只有两种选择，即装入背包、不装入背包。不 能将物品 i 装入背包多次，也不能只装入部分的物品 i。该问题称为 0/1 背包问题。

3.2 问题的符号化

3.3 问题解决

闫式dp分析法 :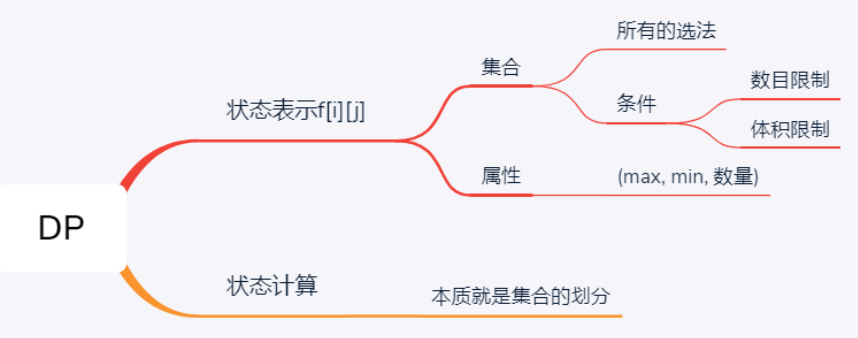

背包问题dp分析

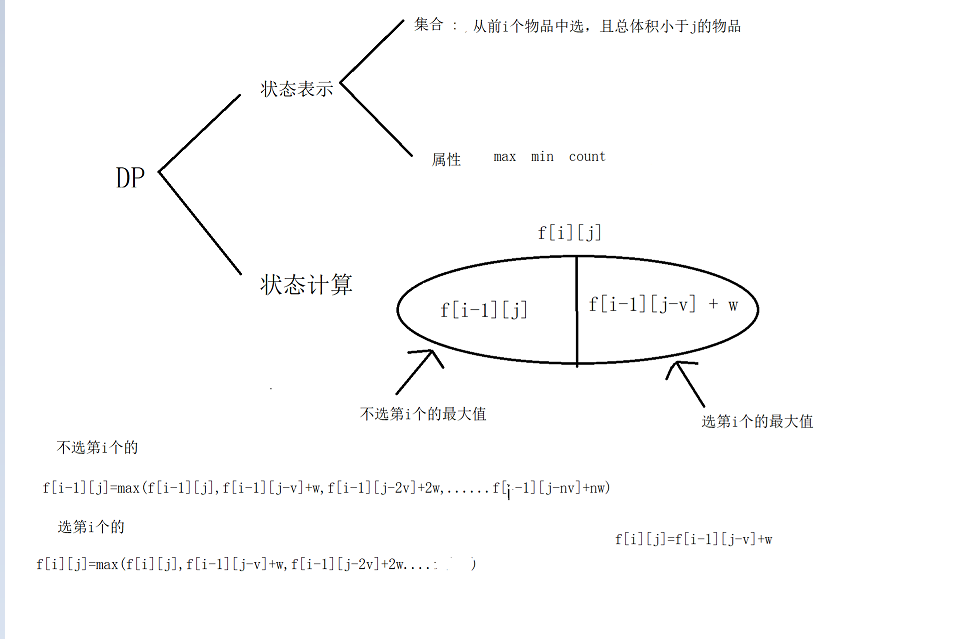
3.4 代码

3.4.1 代码1

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int f[N][N]; //状态转移方程
int v[N] , w[N];
int n ,m; // n 代表物品个数，m代表背包体积

int main() {
    cin >> n >> m;

    for (int i = 1 ; i <= n ; i ++ ) cin >> w[i] >> v[i];
    for (int i = 1 ; i <= n ;  i++ ) { //i从1开始因为下面会用到i - 1 ，避免数组下标越界
        for (int j = 1 ; j <= m ; j ++ ) {
            f[i][j] = f[i - 1][j]; //初始f[i][j] = f[i - 1][j]; //上一个状态的最大值
            if (j >= w[i]) f[i][j] = max(f[i][j] , f[i - 1][j - w[i]] + v[i]);
        }
    }
    cout << f[n][m] << endl;
}

3.4.2 滚动数组优化

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int f[N]; //状态转移方程
int v[N] , w[N];
int n ,m; // n 代表物品个数，m代表背包体积

int main() {
    cin >> n >> m;

    for (int i = 1 ; i <= n ; i ++ ) cin >> w[i] >> v[i];
    for (int i = 1 ; i <= n ;  i++ ) { //i从1开始因为下面会用到i - 1 ，避免数组下标越界
        for (int j = m ; j >= w[i] ; j -- ) {
           f[j] = max(f[j] , f[j - w[i]] + v[i]);
        }
    }
    cout << f[m] << endl;
}

关于滚动数组优化为什么要逆序的原因 : 
for (int i = 1 ; i <= n ;  i++ ) { //i从1开始因为下面会用到i - 1 ，避免数组下标越界
        for (int j = m ; j >= w[i] ; j -- ) {
           f[j] = max(f[j] , f[j - w[i]] + v[i]);
        }
    }

1 . f数组的后半部分，f[j~m]处于'第i个阶段'，也就是已经考虑过放入第i个物品的情况.
2 . 前半部分 f[0~j-1]处于'第i-1个阶段',也就是还没有第i个物品更新
    接下来j不断减小，意味着我们总是用'第i-1个阶段'的状态向'第i个阶段'的状态进行转移,符合线性DP的原则，进而保证了第i个物品只会被放入背包一次



如果采用正序的话 : 
然而，如果使用正序循环，假设f[j]被f[j-vi]+wi更新，接下来j增大到j+vi时，f[j+vi]又可能被f[j]+wi更新。此时,两个都处于'第i个阶段'的状态之间发生了转移，违背了线性dp的原则，相当于第i个物品被使用了两次
    f[j-vi] = f[j-2vi]+wi;//不选第i个
    f[j]=f[j-vi]+wi=f[j-2vi]+2wi;//选第i个

    f[j] = f[j-vi]+wi;
    f[j+vi]=f[j]+wi;
    f[j]和f[j-vi]+wi比更新了一次 ， 然后j增大到j+vi时 f[j]再次使用了一次

上述陈述摘自算法竞赛进阶指南