引言

现代计算机基于冯诺依曼模型，机器内部采用二进制编码。采用二进制编码的好处是，物理器件的设计变得简单，只要通过高低电平就能够表示0和1两个状态，0与1正好表示逻辑真值，逻辑门电路也可以容易实现。在网络传输中，由于存在噪声等干扰，01二进制具有最大的离散化，因此坑噪声能力强。

计算机内部只有整数、浮点数和位串三种数据，而在计算机用户来看，计算机可以处理数值、图像、声音、视频等复杂数据与信息。数据的层次如下图所示：

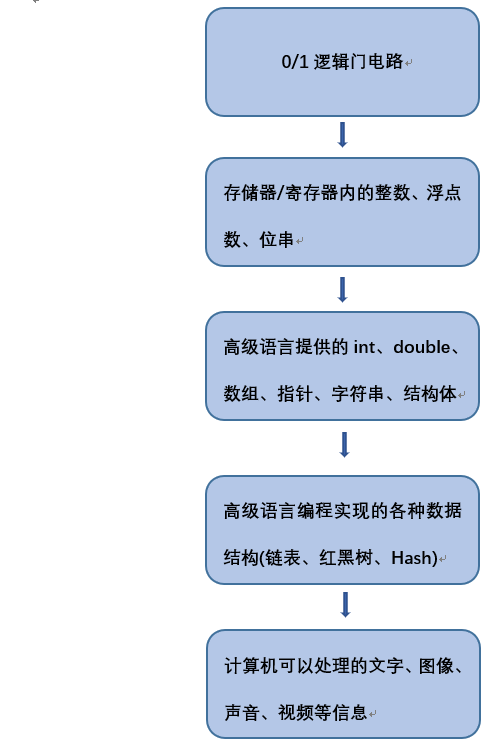
进制

数学中一般采用十进制表示数字，例如：123.45代表的值为$1\times10^3 + 2\times 10^2 + 3\times 10^1 + 4\times 10^{-1} + 5\times 10^{-2}$。不同位上有不同的权重，从右到左每次提高10倍。这里面10称为基数，$10^i$称为第$i$位上的权。

类似的，计算机采用的二进制，例如：$(1101.01)_2 $表示的数值为：$1\times 2^4 + 1\times 2^3 + 0\times 2^2 + 1\times 2^1 + 0\times 2^{-1} + 1\times 2^{-2} =13.25$。

一般地可以定义R进制数，采用R个基本符号，采用逢R进1的运算规则。

计算机系统的常用进制：

• 二进制，基本符号为0、1，在C语言中用0b开头
• 八进制，基本符号为0、1、2、3、....7，C语言中以$o$开头
• 十六进制，基本符号为0、1、…、9、A、B、C、…、F，以0x开头

二进制与十进制之间的转换

二进制转换为十进制比较简单，只要按权展开计算即可。

十进制转化为二进制，采用带余除法，不断用基数除商，最后将余数倒置即可。例如：将13转化为二进制数的过程如下：

• 13除2，商6余1
• 6除2，商3余0
• 3除2，商1余1
• 1除2，商0余1

余数依次是1、0、1、1，因此二进制表示为1101。

如果用代码计算，可以如下：

void decimal_to_binary(int x) {
    printf("十进制表示为: %d\n", x);
    int t[32];
    for (int i = 0; i < 32; i++)
        t[i] = x >> i & 1;
    printf("二进制表示为: ");
    for (int i = 31, flag = 0; i >= 0; i--) {
        if (t[i]) flag = 1;
        if (flag) printf("%d", t[i]);
    }
}

带小数的转换

二进制转换为十进制依旧按权展开，十进制转为二进制，可以将整数部分和小数部分分开计算，最后拼接在一起。小数部分采用乘基取整，每次乘基数，保留小数部分。例如将$(0.6875)$转换为二进制：

• $0.6875\times 2 = 1.375$，整数部分为1
• $0.375\times 2 = 0.75$，整数部分为0
• $0.75\times 2 = 1.5$，整数部分为1
• $0.5\times 2 = 1$， 整数部分为1

最终的结果为:$(0.1011)_2 $

二进制、八进制、十六进制之间的转换

由于二进制表示的数字位数太长不便于阅读，因此也常常用八进制和十六进制表示数字。以二进制和十六进制之间转换为例，其余完全类似。二进制转换为十六进制每4为转为一个十六进制数字，如果不足4位用0填充，十六进制转为二进制，每位转换位对应的4位二进制数。例如：$(1011 0011)_2$转为十六进制为$(B3)_{16}$ ，因为1011表示十进制11，而11的十六进制表示为B，0011的十进制表示和十六进制都是3。

小数点固定的数成为定点数，计算机中用定点数表示整数。小数点位置可以改变的成为浮点数，计算机采用浮点数表示实数。

原码、补码、反码、移码

整数包含负数，因此在原码表示中，需要一个单独的位表示符号，如果该位为1则表示一个负数，反之为正数。这种用符号用0/1表示的方式称为符号数字化。

数值数据在机器内部编码后的表示称为机器数，机器数对应的数值称为真值。

相同的数值数据可以采用不同的编码方式，不同的编码方式有其各自的优点与不足。就实际而言，整数采用补码表示，而实数采用的浮点数表示中，包含了原码、移码。

原码表示

用最高位来表示符号位，剩余位表示数值。例如$(1010)$符号位是1，表示负数，010表示2，因此真值为-3。

从原码表示的定义中可以看出，其对应关系比较直观，鲤鱼程序员阅读和理解。

但是，采用补码表示的0有两个，$-0$和$+0$，这样能够表示的状态数就少了，但更重要的是，原码的加减运算复杂。需要对运算的两个数的绝对值进行判断，然后才能够确定结果的符号，这样电路的设计复杂，难于实现。

补码表示

如果将减法看成是加上一个负数，那么加减运算就可以简化为同一种运算，而补码可以实现该统一。计算机的补码表示也称为2-补码，与之对应的是变形补码，也叫做模4补码。

计算机内部所有的运算都是在寄存器上进行的，而由于寄存器的物理限制，只能存储有限固定的位数。如果运算结果超过了能够表示的范围就发生了溢出。当发生溢出时，保留低位，将高位舍弃。例如在十进制中，如果只有两位，$68+54 = 122 = 22$，高位丢弃后变为22，所以可以看成对所有的运算结果模100。同理如果寄存器的位数位n，运算结果是一个模$2^n$的运算系统。在这个系统中，如果超出了表示范围，实际表示的数是经过$2^n$平移到可表示范围内代表的数。

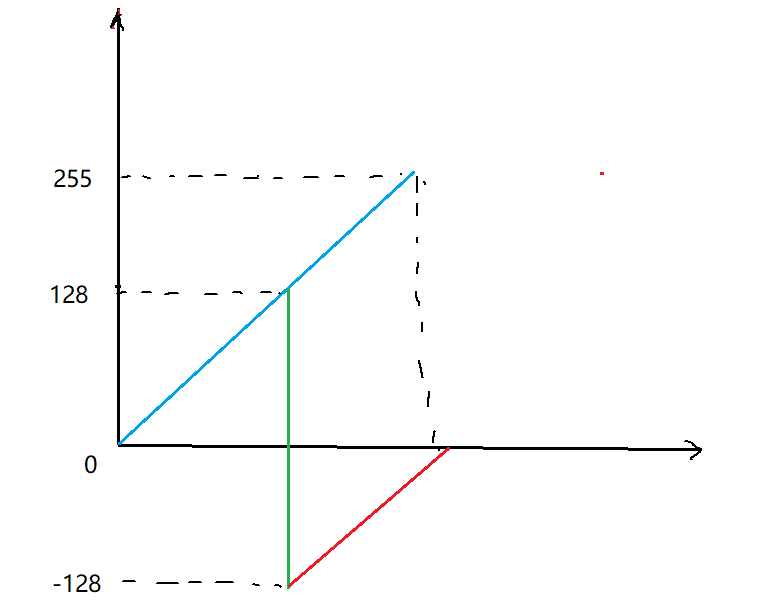
上图表示补码的范围，以8位补码为例。
如果采用无符号表示整数，8位可以表示范围是$(00000000)$到$(11111111)$，也就是十进制的0到255。这8位二进制数最多能够表示255个状态。如果超过255，就要重新计数，例如$258 = 256 + 2$，因此溢出后实际表示的数为2。所有相互之间相差256的数在模256意义下都是同一个数(数学中的同余)，所有同余系构成了一个等价类。

补码表示中，从128开始对数据进行模运算，将其统一减去256，这样做以后。补码可以表示范围从$[0,255]$变为$[-128,127]$。

这样，任意的整数都可以平移到补码表示的范围中，例如：-150不在补码范围中，因此对其加256，对应真值为106；996不在$[-128,127]$的范围中，平移4个256 = 1024， $996 -1024 = -28$。所以996用8位补码表示后，其真值是-28。

反码表示

将各位取反得到的就是反码表示，补码可以通过反码+1得到。反码可以看成求补码的一个中间步骤，在计算机中补码很少能直接用到，有时会在数据校验中出现。

移码表示

浮点数的阶一般用移码表示，一个浮点数的指数部分可正可负，为了同一用整数编码，将代表其加上一个正常数，称为偏置常数。即：$E_{移} = E + 偏置常数$，具体见浮点数的表示

整数的表示

无符号整数

如果一个二进制表示中，所有位都是数值位，这样的编码表示的数就是无符号数。对于一个n位的无符号数$a_{n-1}…a_2a_1a_0$表示的数为：$a_{n-1}\times 2^{n-1} + a_{n-2}\times 2^{n-2}+\cdots + a_1 \times 2^1 +a_0 \times 2^0$。

带符号整数

带符号数在计算机内部用补码表示，一个n位补码数$a_{n-1}…a_2a_1a_0$表示的数值为：$-a_{n-1}\times 2^{n-1} + a_{n-2}\times 2^{n-2}+\cdots + a_1 \times 2^1 +a_0 \times 2^0$，最高位的权重是负值$-2^{n-1}$。或者还可以写成：$-2^{n}+a_{n-1}\times 2^{n-1} + a_{n-2}\times 2^{n-2}+\cdots + a_1 \times 2^1 +a_0 \times 2^0$，如果最高位是1，则其表示的数值需要减去$2^n$，这正是补码是一个模$2^n$运算系统的体现。

补码表示有以下几个特点：

• 如果最高位是0，则表示一个正数

• 如果最高位是1，则表示一个负数

• 最小的负数比最大的正数绝对值大1，例如8位补码整数，最小值-128，最大值127
• -(MIN) = MIN，对一个数取负后，不一定是正数，当取最小负数时就不满足了
• 如果一个编码中最高位是1，那么在前面加上若干的1数值不变，在C中常用的memset函数里，如果将每个字节赋值为$-1$，一个字节的编码为$11111111$，而int有4个字节，一共32个1，这样表示的数值还是$-1$。

在C语言中规定，带符号整数和无符号整数之间运算，会先将带符号整数转为无符号数，然后进行运算。

浮点数的表示

在计算机发展早期并不能很好的处理小数运算，因为小数是连续的，而计算机只能处理有限离散值。

浮点数的存储以及加减乘除运算是一个比较复杂的问题，很多小的处理器在硬件指令方面甚至不支持浮点运算，其他的则需要一个独立的协处理器来处理这种运算，只有最复杂的处理器才会在硬件指令集中支持浮点运算。省略浮点运算，可以将处理器的复杂度减半，如果硬件不支持浮点运算，那么只能通过软件来实现，代价就是需要容忍不良的性能。

作为处理器行业的老大，Intel 早就意识到了这个问题，并打算一统浮点数的世界。Intel 在研发 8087 浮点数协处理器时，聘请到加州大学伯克利分校的 William Kahan 教授（最优秀的数值分析专家之一）以及他的两个伙伴，来为 8087 协处理器设计浮点数格式，他们的工作完成地如此出色，设计的浮点数格式具有足够的合理性和先进性，被 IEEE 组织采用为浮点数的业界标准，并于 1985 年正式发布，这就是 IEEE 754 标准，它等同于国际标准 ISO/IEC/IEEE 60559。

现在的计算机都支持IEEE754标准，在IEE754标准中，浮点数被划分为了三类：

• 规格化浮点数
• 非规格和浮点数
• 特殊值

下面以32为浮点数表示为例，64位或者更高位的原理完全类似，只是每个段的位数不同。

在32位的编码中，分成了3段，如下图所示：

对于一个实数$X$，可以表示成如下形式：
$$ X = (-1)^s \times M \times R ^{E} $$
$S$的0/1表示$X$的符号，0为正，1为负。

$E$是一个二进制定点数，称为$X$的阶或指数，$R$是基数，取2。

$M$称为尾数，可以表示数的有效位。

浮点数的表示类似于科学计数法，例如983745.72用科学法表示为：$9.8374572\times 10^5$，都用$x.yz…、\times 10^{n}$这样形式表示，小数点左边固定1位，用$10^{n}$的指数部分将小数点进行移动，使其变为标准形式。浮点数的基数为2，同时整数部分为1。

阶码是一个8位无符号移码，偏置常数为127。因此阶的范围是$[0,255] - 127 = [-127, 128]$。

尾数部分共23位，表示转换为标准形式后，小数点右边的数值。

规格化浮点数

规格化浮点数是浮点数的主要部分，我们通常在代码中使用的小数也是这一部分。按照上面的定义，以一个例子来看：

一个浮点数在机器内部的二进制数为$0 - 10000011 - 001 1101 0000 0000 0000 0000$，中间用杠将各个部分隔开。

符号位$S$为0，因此这是一个正数，阶码$E$为$10000011$，对应的整数是131，由于阶码是用移码来表示的，需要减去偏置得到真实值，$131-127 = 4$，因此指数为4。最后看尾数部分$001 1101 0000 0000 0000 0000$，由于小数点移动了4位，因此小数部分表示为$(1.0011101)_2$，最终表示的数为：$-1^{0} \times 1.0011101\times 2^4 = 10011.101 = 19.625$。

反过来，求19.625的机器数表示，由于是正数，因此符号位是0，19.625用二进制表示为$10011.101$，将小数点进行平移是的整数部分只有1，变为$1.0011101\times 2 ^4$，因此阶码为$4 + 127 = 131 = 10000011$，尾数部分为$0011101$将其补满到23位$001 1101 0000 0000 0000 0000$，所以对应的二进制表示为：$0 - 10000011 - 001 1101 0000 0000 0000 0000$。

非规格和浮点数

如果阶码全为0，则显然表示一个很小的数，实际运算中，为了减小运算误差需要定义更小的浮点数，这就是非规格化浮点数，用来表示在0附近的小数。当阶码全为0时，指数不再表示$0-127 = 2^{-127}$，这样的数了，这时指数部分为$-126$，而尾数的整数部分为0，只有小数部分。

按照定义，规格和浮点数最小可以表示的范围是：$1.000…00\times 2^{-126} - 1.111…11\times 2 ^{-126}$。

而非规格化浮点数的范围是：$0.00…01\times 2^{-126} = 0.111…11\times 2^{-126}$。

采用非规格化的设计后，最小数可以降低$2^{23} = 8,388,608$倍，同时非规格化数和规格化数之间是连续过渡的。

特殊值

如果阶码和尾数全为0，这时表示数值0，符号位可以表示对应的负0和正0。

如果阶码全为1，尾数全为0，这样的表示无穷大，符号位决定正负无穷。

如果阶码全1，尾数不全为0，表示NaN(Not a Number)即不是一个数的数，通常由非不定运算得到，如无穷之间的运算，分母为0，根号里面数为负。

IEE754标准下，可以表示普通小数、接近0的极小数、0、无穷大、非数，这样几乎所有数学运算都可以进行处理了。

32位的浮点数也被称为单精度浮点数，64位的称为双精度浮点数，C语言中用float和double表示。

浮点数的解释通过下面表格展示：

单精度浮点数

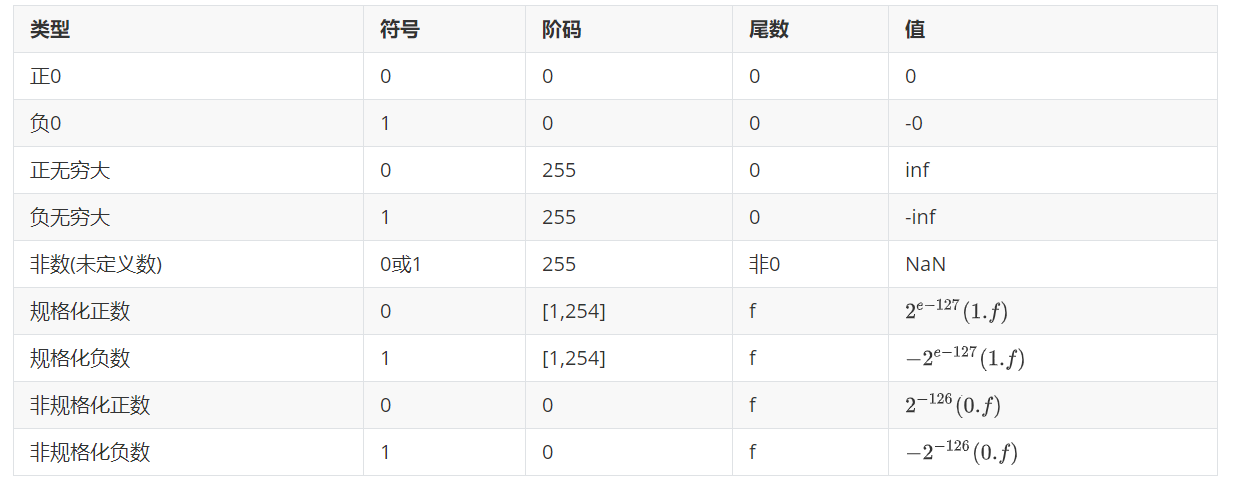
对于双精度浮点数，阶码为11位，尾数52位。双精度浮点数的有效位数有15位左右，在计算中如果long long 还会溢出，则在中间计算可以先用double来存储，最后转换为long long ,这样做的前提是有效位数不能超过16位。

浮点数可以表示的范围如下图所示：

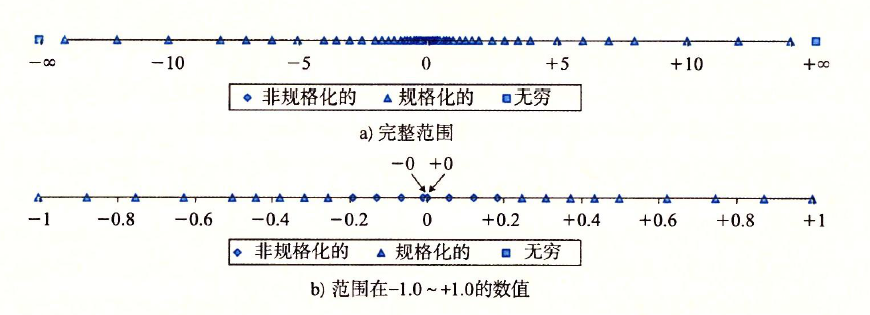
越靠近原点越密集，远离远点则稀疏。

其他数据的表示

十进制表示

虽然计算机内部采用二进制表示，但是在外部是用十进制表示的。十进制数在计算机有多种表示方式：

• ASCII码，将十进制数看成是字符串0-9对应30H-39H，这种表示运算不方便
• BCD码，也称8421码，用4位表示一个十进制数。
• 无权BCD码，没有确定的全，用的最多的是余3码和格雷码

字符的表示

字符由字母、数字、符号组成，字符的集合称为字符集。在对字符进行编码时，每个字符对应一个二进制序列，所有的对应构成了一张表，称为码表。字符主要用于外部设备和计算机之间交换信息，一旦确定了字符集和编码方法后，计算机内部的二进制代码和外部设备和显示设备的字符就可以建立一一对应的关系了。

最早的字符集称为ASCII码，只含有128个字符，无法表示中文等汉字。

像中文这种字符，在计算机用宽字符存储，包含宽字符的字符集有UTF-8等。

在数据进行二进制编码后，得到若干字节的数据。按照字节排放方式的不同可以分成大端和小端。

大端方式：数据的最高有效字节放在小地址单元中。

小端方式：数据的最高有效字节放在大地址单元中。

数据的运算

这部分和数字电路联系较大，有兴趣的同学可以参考相应书籍，这里只做简要介绍。

按位运算

计算机提供与或非等位运算，可以对特定位模式进行提取、置0、置1、清0等操作，这样的位模称为掩码，位运算的更多用法可以参考算法书籍。

逻辑运算

只有True和False两种真值，如果表示非0数，则逻辑真，反之为假。

左移和右移运算

当进行左移时，高位丢弃，低位补0。

右移分为逻辑右移和算数右移，右移时，丢弃低位，逻辑右移高位补0，算数右移高位补符号位。

正数在计算机内部用补码表示，因此可以统一加减运算，都是通过整数加减运算器实现。在运算中运算器的某些位表示运算的状态，例如：零标志(ZF)表示运算结果是否位为0、溢出标志(OF)表示运算过程是否发生了溢出、符号标志(SF)表示运算结果的正负、进/借位标志（CF）表示运算中是否产生了进位/借位。

当运算结果超过了n位寄存器的表示范围，这时发生了溢出。如果像无穷大方向溢出称为正溢出，反之为负溢出。不管是正负溢出，都可以通过平移$2^n$的若干倍到可表示范围内。

对于乘法运算，计算机内部首先用一个2n位保留中间结果，然后截取低n位。乘法可以通过无符号乘法器实现。

由于乘法进行运算时需要10个左右的时钟周期，远大于加减和位移运算。编译器做乘法时会对指令进行优化，例如一个数乘20会转化为$20= 16 + 4$，就可以用加法和位移实现$(x << 4) + (x << 2)$。

对于除法运算，实现更加复杂，并且不能通过流水线的方式实现，一次除法运算大致需要30个或更多的时钟周期。

浮点数的加减运算

浮点数的加减有对阶、尾数加减、尾数规格化、尾数舍入等几步。两个规格化浮点数$x,y$的表示为$x=M_x2^{E_x}$，$M_y2^{E_y}$,不失一般性设$E_x \le E_y$，那么：
$$ x + y = (M_x \times 2^{E_x - E_y} +M_y)\times 2^{E_y} \\ x - y = (M_x \times 2^{E_x - E_y} -M_y)\times 2^{E_y} $$
对阶，对阶的目的是尾数可以进行加减。对阶的原则是：小阶向大阶看起，阶小的数尾数右移，右移的位数等于两个阶的差。

位数加减，对对阶后的尾数进行加减，需要还原隐藏位(1)，对阶过程尾数右移时保留附加位也要参与运算

尾数规格化，在尾数进行加减后可能出现以下情况：
$$ 1.bbb…b+1.bbb..b = +/- 1b.bbb…b\\ 1.bb…b - 1.bb…b = 0.00..0001bbbb $$
对于第一种情况，需要进行右规，同时阶码+1。

对于第二种情况，需要进行左规，阶码逐次减，小数点左移，直至整数部分为1。

尾数的舍入

在进行右规时，低位先不进行舍弃，参与中间运算，最后将运算结果舍入。

浮点数的乘除运算

在运算前需要进行判0处理、规格化操作、溢出判断，确定参与运算的操作数是正常的规格化浮点数。乘除运算与加减运算相比少了对阶的步骤。
$$ x\times y = (M_x \times M_y)\times 2^{E_x +E_y} \\ x / y = (M_x/M_y) \times 2^{E_x - E_y} $$
计算机的浮点数运算复杂，浮点数有规格化非规格化特殊值。利用这些特殊表示，程序可以实现$+\infty +(-\infty)$,$\infty / \infty$，$1/0$等运算。由于浮点数运算中存在对阶、舍入等操作，因而可能导致“大数吃小数”的问题，浮点数运算不能满足加法结合律和乘法交换律。