数据结构之二叉树作业

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

数据结构之二叉树作业

作者：

zmy , 2020-11-15 11:08:52 , 所有人可见 , 阅读 843

6

4

总结一下有关二叉树的部分操作以备不时之需，嘿嘿
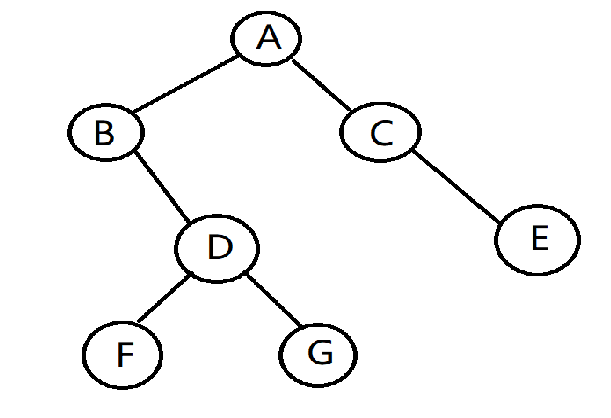
老师布置的一道实验题，题目内容直接搬过来用用
屏幕截图 2020-11-12 215622.png

想要完成上述操作，基本上可根据以下步骤来写

1、造轮子：写出栈结构（用于非递归遍历），队列（用于层次遍历），二叉树的节点结构

1.1 栈结构
首先要知道的是，栈的特点是后进先出，LIFO(Last In First Out)
栈的基本操作：（方便起见，在此借用STL的stack来展示这些操作,$stack<$Typename$> st$）
（1）返回栈顶元素 $st.top()$;
（2）入栈 $st.push(x)$;
（3）出栈 $st.pop()$;
（4）判断栈是否为空栈$st.empty()$;(栈空返回真，否则返回假)

/*栈结构*/
struct Stack {
    bitree* base;
    int top;//栈顶
    int bot;//栈底
    int max_size;
};

1.2 队列结构
队列的特点是先进先出，FIFO(First In First Out)
队列的基本操作：（$queue<$Typename$> q$）
（1）返回队头元素 $q.front()$;
（2）入队$q.push(x)$;
（3）出队$q.pop()$;
（4）判断队列是否为空$q.empty()$;

/*队列结构*/
struct Queue {
    bitree* base;
    int front;
    int tail;
    int max_size;
};

1.3 二叉树的结点结构
（1）数据域
（2）左孩子指针
（3）右孩子指针

/*二叉树结点结构*/
typedef struct Node {
    char Data;
    struct Node* Left_child;
    struct Node* Right_child;
}*bitree, binode;

2、建树（按照二叉树的先序遍历创建二叉树）

根据先序遍历的规则（根左右），依次创建即可,递归创建比较简单，就写递归版的吧

/*递归创建*/
void CreatBiTree(bitree& bt)//按先序遍历创建二叉链表
{
    //根据输入的字符串建立二叉树bt的二叉链表，‘#’表示虚节点
    char ch;
    ch = getchar();
    if (ch == '\n') return;
    if (ch == '#') bt = NULL;
    else {
        bt = new binode;
        bt->Data = ch;
        CreatBiTree(bt->Left_child);
        CreatBiTree(bt->Right_child);
    }
}

3、先序（根、左、右），中序（左、根、右），后序（左、右、根）遍历

3.1 先序遍历
（1）访问根结点；
（2）先序遍历左子树；
（3）先序遍历右子树。

/*递归先序遍历*/
void Pre_Order_Verse(bitree bt)
{
    if (bt != NULL)
    {
        printf("%c", bt->Data);
        Pre_Order_Verse(bt->Left_child);
        Pre_Order_Verse(bt->Right_child);
    }
}

3.2 中序遍历
（1）中序遍历左子树；
（2）访问根结点；
（3）中序遍历右子树。

/*递归中序遍历*/
void Mid_Order_Verse(bitree bt)
{
    if (bt != NULL)
    {
        Mid_Order_Verse(bt->Left_child);
        printf("%c", bt->Data);
        Mid_Order_Verse(bt->Right_child);
    }
}

3.3 后序遍历
（1）后序遍历左子树；
（2）后序遍历右子树；
（3）访问根结点。

/*递归后续遍历*/
void Last_Order_Verse(bitree bt)
{
    if (bt != NULL)
    {
        Last_Order_Verse(bt->Left_child);
        Last_Order_Verse(bt->Right_child);
        printf("%c", bt->Data);
    }
}

5、非递归版遍历

注意：在这里维护的栈是允许空结点入栈的
5.1 非递归先序遍历
屏幕截图 2020-11-15 101623.png
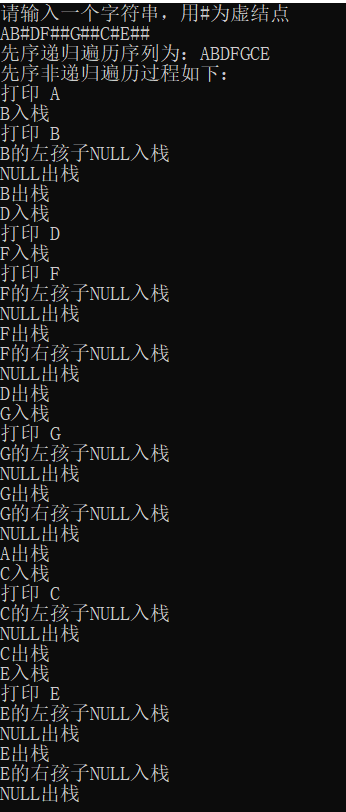
屏幕截图 2020-11-15 100224.png

/*非递归先序遍历*/
void Pre_Inorder_Verse(bitree bt)
{
    Stack st;
    bitree p;
    if (bt)
    {
        Init_Stack(st);
        Push_Stack(st, bt);
        while (!Empty_Stack(st))
        {
            while (Get_Stack_top(st, p) && p != NULL)
            {
                Push_Stack(st, p->Left_child);
            }
            Pop_Stack(st, p);
            if (!Empty_Stack(st))
            {
                Pop_Stack(st, p);
                Push_Stack(st, p->Right_child);
            }
        }
    }
}

5.2 非递归中序遍历
遍历方法和先序遍历类似，不过是按照左根右来遍历即可，代码实现也只是将访问结点的那句代码移动一下位置即可，在这里就不再细述了。

/*非递归中序遍历*/
/*非递归后序遍历*/
void Last_Inorder_Verse(bitree bt)
{
    Stack st;
    bitree p1, p2;
    if (bt)
    {
        Init_Stack(st);
        Push_Stack(st, bt);
        while (!Empty_Stack(st))
        {
            while (Get_Stack_top(st, p1) && p1 != NULL)
            {
                Push_Stack(st, p1->Left_child);
            }
            Pop_Stack(st, p1);//pop掉最左端的空结点
            if (!Empty_Stack(st))
            {
                Get_Stack_top(st, p1);
                Push_Stack(st, p1->Right_child);//将结点的右放入栈中
                if (Get_Stack_top(st, p1) && p1 == NULL)//若结点的右是空，pop掉右，打印结点，若非空，后续遍历右子树
                {
                    Pop_Stack(st, p1);
                    Pop_Stack(st, p1);
                    printf("%c", p1->Data);
                    /*上一次出栈结点是当前栈顶结点的右孩子的处理*/
                    while (!Empty_Stack(st) && Get_Stack_top(st, p2) && p2->Right_child == p1)
                    {
                        Pop_Stack(st, p1);
                        printf("%c", p1->Data);
                    }

                    if (!Empty_Stack(st))
                    {
                        Get_Stack_top(st, p1);
                        Push_Stack(st, p1->Right_child);
                    }
                }
            }
        }
    }
}

6、层次遍历（BFS的方法依次遍历即可）

这个最好写了，直接就是BFS的常规操作啊。直接不多言

/*层次遍历*/
void Level_Traversal(bitree bt)
{
    Queue q;
    Init_Queue(q);
    Push_Queue(q, bt);
    bitree p;
    while (!Empty_Queue(q))
    {
        Pop_Queue(q, p);
        if (p != NULL)
        {
            printf("%c", p->Data);
        }
        if (p->Left_child != NULL) Push_Queue(q, p->Left_child);
        if (p->Right_child != NULL) Push_Queue(q, p->Right_child);
    }
}

7、计算叶子结点的个数（左右都为空的结点）

当左右孩子都是空，该结点就是叶子，记录数量

/*遍历计算叶子结点个数*/
void LeavesCount(bitree bt,int &count)
{
    if (bt != NULL)
    {
        LeavesCount(bt->Left_child, count);
        if (bt->Left_child == NULL && bt->Right_child == NULL) count++;
        LeavesCount(bt->Right_child, count);
    }
}

放上实现作业中要求的所有代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define STACK_SIZE 50
#define QUEUE_SIZE 50
using namespace std;

/*二叉树结点结构*/
typedef struct Node {
    char Data;
    struct Node* Left_child;
    struct Node* Right_child;
}*bitree, binode;

/*栈结构*/
struct Stack {
    bitree* base;
    int top;//栈顶
    int bot;//栈底
    int max_size;
};

/*队列结构*/
struct Queue {
    bitree* base;
    int front;
    int tail;
    int max_size;
};

/*初始化队列*/
void Init_Queue(Queue& q)
{
    q.base = new bitree[QUEUE_SIZE];
    q.front = q.tail = 0;
    q.max_size = QUEUE_SIZE;
}

/*初始化栈*/
void Init_Stack(Stack& st)
{
    st.base = new bitree[STACK_SIZE];
    st.top = 0;
    st.bot = 0;
    st.max_size = STACK_SIZE;
}

/*判栈空*/
bool Empty_Stack(Stack st)
{
    if (st.top == 0) return true;
    else return false;
}

/*判队列空*/
bool Empty_Queue(Queue q)
{
    if (q.front == q.tail) return true;
    else return false;
}

/*入队操作*/
void Push_Queue(Queue& q, bitree e)
{
    if (q.tail > q.max_size)
    {
        bitree* tmp = new bitree[q.max_size + QUEUE_SIZE];
        for (int i = q.front;i < q.tail;i++)//原数据拷贝到新地址
        {
            tmp[i - q.front] = q.base[i];
        }
        int len = q.tail - q.front;
        q.base = tmp;//指针指向新地址
        q.front = 0;q.tail = len;//更改现有队头队尾指针
    }
    q.base[q.tail++] = e;
}

/*入栈操作*/
void Push_Stack(Stack& st,bitree e)
{
    if (st.top - st.bot >= st.max_size)
    {
        bitree* tmp = new bitree[st.max_size + STACK_SIZE];
        for (int i = 0;i < st.max_size;i++) tmp[i] = st.base[i];//原数据拷贝
        st.base = tmp;//指向更大的内存块
    }
    st.base[st.top++] = e;
}

/*出队操作*/
void Pop_Queue(Queue& q, bitree& e)
{
    if (q.tail == q.front)
    {
        cout << "Error Error Error!!!" << endl;
        exit(0);
    }
    else {
        e = q.base[q.front++];
    }
}

/*出栈操作*/
void Pop_Stack(Stack& st, bitree& e)
{
    if (st.top > 0) e = st.base[--st.top];
    else
    {
        cout << "Error Error !!!" << endl;
        exit(0);
    }
}

/*返回队头元素*/
bool Get_Queue_top(Queue q,bitree& e)
{
    if (Empty_Queue(q)) return false;
    else {
        e = q.base[q.front];
        return true;
    }
}

/*返回栈顶元素*/
bool Get_Stack_top(Stack st,bitree& e)
{
    if (Empty_Stack(st)) return false;
    else {
        e = st.base[st.top - 1];
        return true;
    }
}


/*递归创建*/
void CreatBiTree(bitree& bt)//按先序遍历创建二叉链表
{
    //根据输入的字符串建立二叉树bt的二叉链表，‘#’表示虚节点
    char ch;
    ch = getchar();
    if (ch == '\n') return;
    if (ch == '#') bt = NULL;
    else {
        bt = new binode;
        bt->Data = ch;
        CreatBiTree(bt->Left_child);
        CreatBiTree(bt->Right_child);
    }
}

/*递归先序遍历*/
void Pre_Order_Verse(bitree bt)
{
    if (bt != NULL)
    {
        printf("%c", bt->Data);
        Pre_Order_Verse(bt->Left_child);
        Pre_Order_Verse(bt->Right_child);
    }
}

/*递归中序遍历*/
void Mid_Order_Verse(bitree bt)
{
    if (bt != NULL)
    {
        Mid_Order_Verse(bt->Left_child);
        printf("%c", bt->Data);
        Mid_Order_Verse(bt->Right_child);
    }
}

/*递归后续遍历*/
void Last_Order_Verse(bitree bt)
{
    if (bt != NULL)
    {
        Last_Order_Verse(bt->Left_child);
        Last_Order_Verse(bt->Right_child);
        printf("%c", bt->Data);
    }
}

/*非递归先序遍历*/
void Pre_Inorder_Verse(bitree bt)
{
    Stack st;
    bitree p;
    if (bt)
    {
        Init_Stack(st);
        Push_Stack(st, bt);
        while (!Empty_Stack(st))
        {
            while (Get_Stack_top(st, p) && p != NULL)
            {
                printf("%c", p->Data);
                Push_Stack(st, p->Left_child);
            }
            Pop_Stack(st, p);
            if (!Empty_Stack(st))
            {
                Pop_Stack(st, p);
                Push_Stack(st, p->Right_child);
            }
        }
    }
}

/*非递归中序遍历*/
void Mid_Inorder_Verse(bitree bt)
{
    Stack st;
    bitree p;
    if (bt)
    {
        Init_Stack(st);
        Push_Stack(st, bt);
        while (!Empty_Stack(st))
        {
            while (Get_Stack_top(st, p) && p != NULL)
            {
                Push_Stack(st, p->Left_child);
            }
            Pop_Stack(st, p);
            if (!Empty_Stack(st))
            {
                Pop_Stack(st, p);
                printf("%c", p->Data);
                Push_Stack(st, p->Right_child);
            }
        }
    }
}

/*非递归后序遍历*/
void Last_Inorder_Verse(bitree bt)
{
    Stack st;
    bitree p1, p2;
    if (bt)
    {
        Init_Stack(st);
        Push_Stack(st, bt);
        while (!Empty_Stack(st))
        {
            while (Get_Stack_top(st, p1) && p1 != NULL)
            {
                Push_Stack(st, p1->Left_child);
            }
            Pop_Stack(st, p1);//pop掉最左端的空结点
            if (!Empty_Stack(st))
            {
                Get_Stack_top(st, p1);
                Push_Stack(st, p1->Right_child);//将结点的右放入栈中
                if (Get_Stack_top(st, p1) && p1 == NULL)//若结点的右是空，pop掉右，打印结点，若非空，后续遍历右子树
                {
                    Pop_Stack(st, p1);
                    Pop_Stack(st, p1);
                    printf("%c", p1->Data);
                    /*上一次出栈结点是当前栈顶结点的右孩子的处理*/
                    while (!Empty_Stack(st) && Get_Stack_top(st, p2) && p2->Right_child == p1)
                    {
                        Pop_Stack(st, p1);
                        printf("%c", p1->Data);
                    }

                    if (!Empty_Stack(st))
                    {
                        Get_Stack_top(st, p1);
                        Push_Stack(st, p1->Right_child);
                    }
                }
            }
        }
    }
}


/*遍历计算叶子结点个数*/
void LeavesCount(bitree bt,int &count)
{
    if (bt != NULL)
    {
        LeavesCount(bt->Left_child, count);
        if (bt->Left_child == NULL && bt->Right_child == NULL) count++;
        LeavesCount(bt->Right_child, count);
    }
}

/*层次遍历*/
void Level_Traversal(bitree bt)
{
    Queue q;
    Init_Queue(q);
    Push_Queue(q, bt);
    bitree p;
    while (!Empty_Queue(q))
    {
        Pop_Queue(q, p);
        if (p != NULL)
        {
            printf("%c", p->Data);
        }
        if (p->Left_child != NULL) Push_Queue(q, p->Left_child);
        if (p->Right_child != NULL) Push_Queue(q, p->Right_child);
    }
}

/*主函数*/
int main()
{
    bitree root;
    cout << "请输入一个字符串，用#为虚结点" << endl;
    //根据输入的字符串建立二叉树的二叉链表，#表示虚结点
    CreatBiTree(root);
    int ans = 0;
    LeavesCount(root, ans);
    cout << "该二叉树的叶子节点个数为：" << ans << endl;
    /*先序遍历*/
    cout << "先序递归遍历序列为：";
    Pre_Order_Verse(root);puts("");
    cout << "先序非递归遍历序列为：";
    Pre_Inorder_Verse(root);puts("");
    /*中序遍历*/
    cout << "中递归遍历序列为：";
    Mid_Order_Verse(root);puts("");
    cout << "中序非递归遍历序列为：";
    Mid_Inorder_Verse(root);puts("");
    /*后序遍历*/
    cout << "后序递归遍历序列为：";
    Last_Order_Verse(root);puts("");
    cout << "后序非递归遍历序列为：";
    Last_Inorder_Verse(root);puts("");
    /*层次遍历*/
    cout << "层次遍历序列为：";
    Level_Traversal(root);puts("");
    return 0;
}

0 评论

App 内打开