连通分量：在有向图中，对于分量中任意两点$u,v$，必然可以从u走到v，且从v走到u。

强连通分量scc：极大连通分量，极大连通子图。

将图中的边$(x,y)$分为四大类：

1. 树枝边：x是y的父节点
2. 前向边：x是y的祖先节点
3. 后向边：y是x的祖先节点，红色边
4. 横插边：只能往左横插，如果往右横插，在后续遍历肯定会遍历到，因此属于树枝边，绿色边

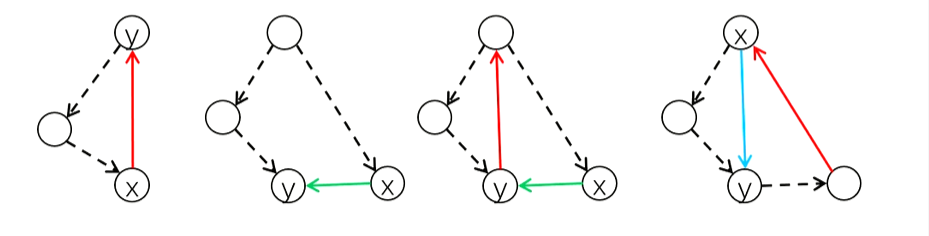
可以发现树枝边和前向边在寻找强连通分量是没有太大用处的，因为本身搜索树本身就

存在这样的路径，而后向边和就很有用。$（x,y）$这样的后向边和$(y,x)$这样的边可

以构成一个环。

横插边在有些情况有用，有些情况没用。

引入时间戳$dfn$

按dfs顺序给每个点一个编号。

对于每个点定义两个时间戳：

$dfn[u]$:遍历到u的时间戳

$low[u]$:从u开始走，所能走到的最小时间戳是什么。

u是其所在强连通分量的最高点，等价于$dfn[u]==low[u]$

时间复杂度：$O(n+m)$

#include<bits/stdc++.h>
#define rep(x,y,z)  for(int x=(y);x<=z;x++)
#define fep(x,y,z)  for(int x=(y);x>=z;x--)
#define db double
#define ll long long
#define pii pair<int,int>
using namespace std;
const int N=1e5+10,M=N<<1,INF=0x3f3f3f3f,MOD=1000000007;
int h[N],e[M],ne[M],idx;
int n,m;
int stk[N],ins[N],c[N],top,cnt;
int dfn[N],low[N],tot;
vector<int>scc[N];

void add(int a,int b)
{
    e[++idx]=b,ne[idx]=h[a],h[a]=idx;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    stk[++top]=u;ins[u]=1;
    for(int i=h[u];i;i=ne[i])
    {
        int ver=e[i];
        if(!dfn[ver])
        {
            tarjan(ver);
            //离开时更新low
            low[u]=min(low[u],low[ver]);
        }
        else if(ins[ver])   low[u]=min(low[u],dfn[ver]);    
    }
    if(dfn[u]==low[u])
    {
        ++cnt;int y;
        do{
            y=stk[top--],ins[y]=0;
            c[y]=cnt,scc[cnt].push_back(y);
        }while(u!=y);
    }
}

void solve()
{
    cin>>n>>m;
    rep(i,1,m)
    {
        int a,b;cin>>a>>b;
        add(a,b);       
    }
    for(int i=1;i<=n;++i)
        if(!dfn[i]) tarjan(i);
    int ans=0;
    for(int i=1;i<=cnt;++i)
    {
        if(scc[i].size()==1)    ans++;  
    }   
    cout<<ans<<'\n';
    return;
}   

int main()
{
//    freopen("1.in","r",stdin);
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    solve();
    return 0;
}