什么是AC自动机

AC自动机故名思意，就是可以自动AC代码的机器。

开个玩笑，AC自动机其实是一个状态转移，该机器可以根据输入自动改变内部状态，并输出最终状态。
AC自动机的状态转移可以看成是一个拓扑图，一个简单的状态转移如下图所示：

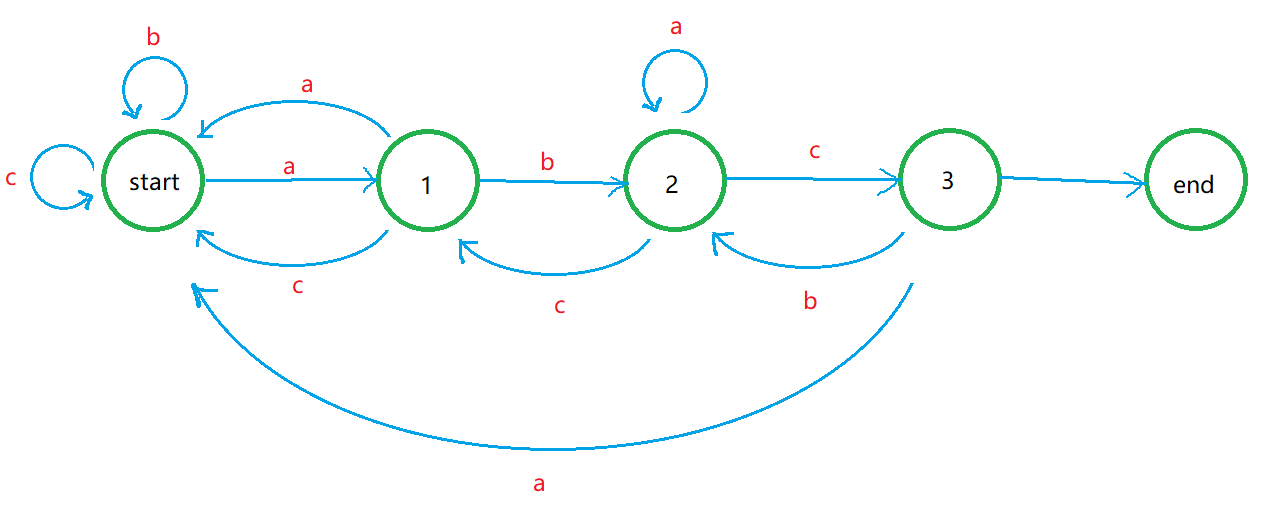
start表示起始状态，end表示出口状态，其余1、2、3都表示机器可以到达的状态。

例如输入为cacabac，状态转移如下：

• 起始状态为start，第一个字符为c，因此第一步停在原地start
• 第二个字符为a，这回可以前进了，到达状态1
• 第三个字符为c，跳回状态0(start)
• 第四个字符为a，转移到1
• 第五个字符为b，转移到2
• 第六个字符为c，转移到2
• 第七个字符为c，转移到3，并自动到达出口end

特别地，了解KMP原理的同学可以发现，如果abc表示模式字符串，则到达出口end表示一个字符串匹配成功。

那么这和AC自动机有啥关系呢？上面不就是个简单的状态转移图吗？是的，AC自动机其实并没有新的内容，只是我们看待问题的眼光不同了。

如果将构建状态转移图的过程看成，制造一台AC自动机，一旦AC自动机生成，模式匹配问题可以看成向这台机器进行输入，然后机器内部状态自动进行改变，最后输出最终状态。

这个过程形象化的如下图所示：

还可以知道，1、由于输入字符串长度和内部状态有限，因此机器一定会停机。2、一台AC自动机只能处理同一类模式匹配问题，因此我们可以构建多台机器，根据问题的不同交给相应的机器。

一道练习题

以AcWing1053.修复DNA为例。

由题意可知，先建立字典树，将每个单词结尾进行标记，表示该点为致病片段不可达。

接下来构建AC自动机，构建的目的是根据next数组的定义，如果一个单词的后缀是致病片段，那么该点也要被标记，这样标记出所有非法节点。

原题要求最少的改动可以不包含致病片段，就是从树根出发，每一步可以选择ATCG中的任何一个。

如果第k步选择的字符和DNA片段的相同，说明这一步没有修改，代价为0，反之为1。

一共走$m = len(DNA)$步，前提是不能走到被标记的节点，这样所有走法中的最小代价。

采用DP即可，状态转移方程如下：

if (!st[trie[u][i]])
    res = min(res, dp(trie[u][i], len + 1) + (id[s[len]] == i ? 0 : 1));

表示下一步必须选择没被标记的点转移，代价为0或1取决于这一步选择的字符。

$dp(u,v)$表示从节点$u$出发，当前走到第$v$步，到终点所有走法的最小代价。终点的含义为走了m步，且没有经过标记点的一种走法。

代码：

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;
const int N = 1005, INF = 1e9;
int n, m, id[N], trie[N][4], st[N], tot = 0, ne[N];
int f[N][N];
char s[N];
queue<int> q;

void insert() {
    int p = 0;
    for (int i = 1; i <= m; i++) {
        int ch = id[s[i]];
        if (!trie[p][ch]) trie[p][ch] = ++tot;
        p = trie[p][ch];
    }
    st[p] = 1;
}

void build() {
    for (int i = 0; i < 4; i++)
        if (trie[0][i]) q.push(trie[0][i]);
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        for (int i = 0; i < 4; i++) {
            if (trie[t][i]) {
                ne[trie[t][i]] = trie[ne[t]][i];
                if (st[ne[trie[t][i]]]) st[trie[t][i]] = 1;
                q.push(trie[t][i]);
            } else trie[t][i] = trie[ne[t]][i];
        }
    }
}

int dp(int u, int len) {
    if (len == m + 1) return f[u][len] = 0;
    if (f[u][len] != -1) return f[u][len];
    int res = INF;
    for (int i = 0; i < 4; i++)
        if (!st[trie[u][i]])
            res = min(res, dp(trie[u][i], len + 1) + (id[s[len]] == i ? 0 : 1));
    return f[u][len] = res;
}

int main() {
    id['T'] = 1, id['C'] = 2, id['G'] = 3;
    int cnt = 0;
    while (scanf("%d", &n), n) {
        tot = 0;
        memset(ne, 0, sizeof ne);
        memset(st, 0, sizeof st);
        memset(trie, 0, sizeof trie);
        memset(f, -1, sizeof f);
        for (int i = 1; i <= n; i++) {
            scanf("%s", s + 1);
            m = strlen(s + 1);
            insert();
        }
        build();
        scanf("%s", s + 1);
        m = strlen(s + 1);
        int res = dp(0, 1);
        printf("Case %d: %d\n", ++cnt, res == INF ? -1 : res);
    }
    return 0;
}