Union-Find Set（并查集）

我们要树立一个学习目标！
1.什么是并查集？
2.Union是什么，有什么含义？
3.Find是什么，有什么作用？
4.这个算法学了能用到哪里？

首先并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Union：将两个子集合并成同一个集合。

为了更加精确的定义这些方法，需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素，称为代表，以表示整个集合。接着，Find(x) 返回 x 所属集合的代表，而 Union 使用两个集合的代表作为参数。

如果你看到这些太过于总结性的话不理解？那么我们来举一个例子：

江湖中人—-并查集

为了解释并查集的原理，我将举一个江湖的例子。 话说在acwing这个大陆上上有各种大佬，有上千万个之多。他们都是小学生，初中生，高中生还有最弱的大学生，但是他们分散世界各地，他们碰到和自己不是一路人的，就免不了要PK一场（手速rank）。但大佬绝对不会去欺负自己的朋友。而且朋友的朋友也是朋友，只要是能通过朋友关系串联起来的，不管关系延长多远，都认为是自己人。这样一来，acwing大陆上就形成了一个一个的团体，通过两两之间的朋友关系串联起来。而不在同一个acwing大陆上的人，无论如何都无法通过朋友关系连起来，于是就可以放心往死了打。但是两个原本互不相识的人，如何判断是否属于同一个acwing大陆的团体呢？

我们可以在每个朋友团体内推举出一个比较有名望的人，作为该圈子的代表人物，这样，每个圈子就可以这样命名“yxc朋友之队”“熊助教朋友之队”秦助教朋友队“……两人只要互相对一下自己的队长是不是同一个人，就可以确定敌友关系了。

（ 我们来看看find函数：）

但是还有问题啊，大大佬们只知道自己直接的朋友是谁，很多人压根就不认识队长，要判断自己的队长是谁，只能漫无目的的通过朋友的朋友关系问下去：“你是不是队长？你是不是队长？”这样一来，大家都在浪费时间找队长，但是我们是来打架的，而且效率太低，还有可能陷入无限循环中。于是队长下令，重新组队。队内所有人实行分等级制度，形成树状结构，我队长就是根节点，下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候，只要一层层向上问，直到最高层，就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否连通，至于他们是如何连通的，以及每个圈子内部的结构是怎样的，甚至队长是谁，并不重要。所以我们可以放任队长随意重新组队，只要不搞错敌友关系就好了。于是，团队产生了。

画个图：

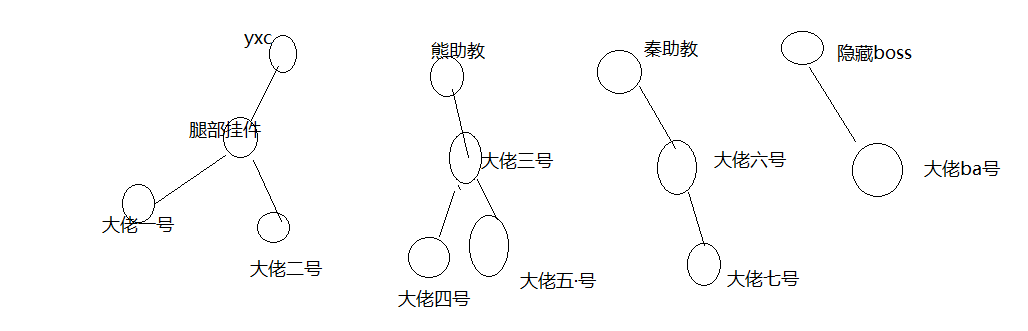
下面我们来看一下并查集怎么去找队长！
我们设一个数组p[N]来存储大佬的上级，例如p[88]=3,说明88号大佬的上级是3号大佬。当然里面还有特殊情况，如果他的上级就是自己，他有可能是队长，或者一人一队，就比如lyd大佬，每一个人认识他的上级，要想知道自己的上级的上级，只能通过自己的上级访问，我们来看一下代码：

递归版：

int find(int x){//找队长
    if(x!=p[x])return find(p[x])//如果自己不是，那么去请求他的上一级
    return x;  //找到了队长
}

非递归：

int find(int x)
{
    while(pre[x]!=x)
      x=pre[x];
    return x;

有一个问题，如果秦助教队里面的大佬朋友想带领这个团队加入yxc老师团队，因为他不想看他们见面就PK,用手速解决问题，所以我们就要让秦助教加入yxc老师队伍里面，所以union函数，就是在两个点之间连一条线，这样一来，原先它们所在的两个板块的所有点就都可以互通了。这在图上很好办，画条线就行了.

代码实现：

void union(int x,int y){
    p[find(x)]=find(y);  //秦助教队长就是y老师
}

路径压缩—节约时间，迫切的想solo

建立团队的过程是用union函数两个人两个人地连接起来的，谁当谁的手下完全随机。最后的树状结构会变成什么模样，是完全无法预计，一条线也有可能。这样查找的效率就会比较低下。最理想的情况就是所有人的直接上级都是队长，一共就两级结构，只要找一次就找到队长了。或者最好尽量接近。这样就产生了路径压缩算法。

他要解决的问题就是因为两个人要询问很久才知道自己的队长，都准备选题solo了，但是最后缺被告知他们队长一样，为下一次不产生只有的误会，他们决定把他们的上一级变为队长，所以整个团队的树高分布就很低，而且查询比较省时间。

画一个图理解一下：

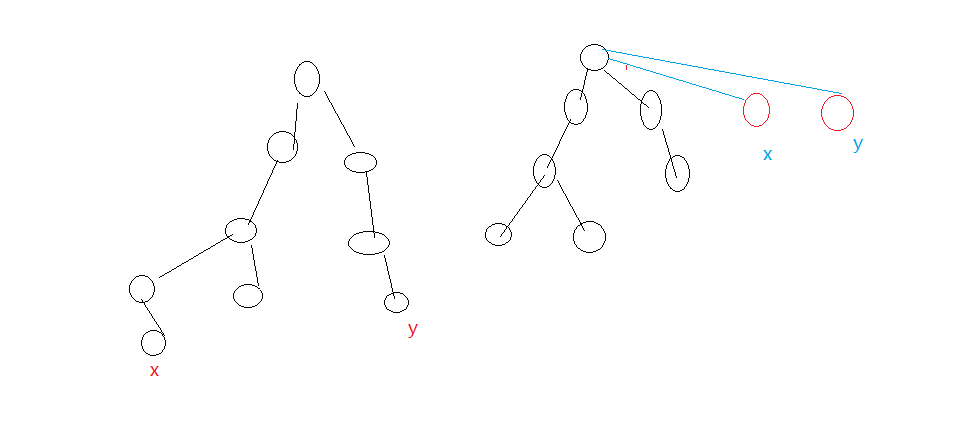
还可以再优化为一个两层的树状结构！！

代码：

int zip(int x)//路径压缩
{
    if(pre[x]!=x)   pre[x]=find(pre[x]);//他直接跟随队长 
    return x;

习题

习题链接

这个题就是简单点找朋友！！

#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int p[N];

int find(int x){
   if(x!=p[x])p[x]=find(p[x]);
   return p[x];
}
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++)p[i]=i;
    while(m--){
        string op;
        int a,b;
        cin>>op>>a>>b;
        if(op=="M")p[find(a)]=find(b);
        else
        {
           if(find(a)==find(b))puts("Yes");
           else puts("No");
        }
    }
    return 0;
}

习题二

题意：求团队个数：

 #include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=100010;
int p[N],size[N];
int find(int x){
    if(x!=p[x])p[x]=find(p[x]);
    return p[x];
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)p[i]=i,size[i]=1;
    while(m--){
        string op;
        int a,b;
        cin>>op;
        if(op=="C")
        {
            cin>>a>>b;
            if(find(a)==find(b))continue;
            size[find(b)]+=size[find(a)];
            p[find(a)]=find(b);
        }
        else if(op=="Q1")
        {
            cin>>a>>b;
            if(find(a)==find(b))puts("Yes");
            else puts("No");
        }
        else{
            cin>>a;
            cout<<size[find(a)]<<endl;
        }
    }
    return 0;
}

习题三

不同团队成员之间的PK!

#include <iostream>

using namespace std;

const int N = 50010;

int n, m;
int p[N], d[N];

int find(int x)
{
    if (p[x] != x)
    {
        int t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;

    int res = 0;
    while (m -- )
    {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);

        if (x > n || y > n) res ++ ;
        else
        {
            int px = find(x), py = find(y);
            if (t == 1)
            {
                if (px == py && (d[x] - d[y]) % 3) res ++ ;
                else if (px != py)
                {
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }
            else
            {
                if (px == py && (d[x] - d[y] - 1) % 3) res ++ ;
                else if (px != py)
                {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }

    printf("%d\n", res);

    return 0;
}

小结

并查集就是要找关联信息，确定他是否在一个集合中？两个集合的合并？
Find优化:
1. 树的深度
总是将更小的树连接至更大的树上。因为影响运行时间的是树的深度，更小的树添加到更深的树的根上将不会增加树的深度除非它们的树的深度相同，单元素的树的深度定义为0，当两棵秩同为r的树联合时，它们的深度r+1。
2.路径压缩
Union:
先设置一个数组(数组)Father[x]，表示x的“父亲”的编号。 那么，合并两个不相交集合的方法就是，找到其中一个集合最父亲的父亲（也就是最久远的祖先），将另外一个集合的最久远的祖先的父亲指向它。

以上就是并查集的基础部分全部内容，谢谢你的阅读，希望你有所收获！

yxc老师模板 链接

1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);


(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    size[b] += size[a];


(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[I] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

作者：yxc
链接：https://www.acwing.com/blog/content/404/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。