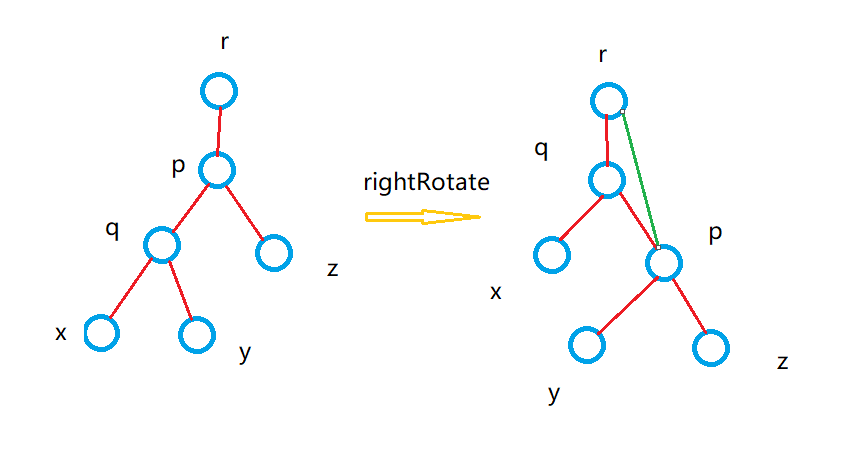
首先来看右旋转的代码:
void zig(int &p) {
int q = a[p].l;
a[p].l = a[q].r, a[q].r = p, p = q;
update(a[p].r), update(p);
}
这是非引用版本,在Treap中,insert或者remove等操作,p都表示当前递归到的根节点。为了让平衡树的高度不太高,就要进行左右旋转来降低树的高度。
如果要对p进行右旋转,如上图所示,旋转后q成为根节点,p已经成为了右子节点。
因此需要将置为q,即代码p = q。但我们知道函数调用是按照值传递的方式进行的。如果仅仅是将p置为q,但函数外并没有得知这个变更信息,所以在外层节点r看来,自己的儿子节点为p,旋转后依然指向p,也就是上图的绿色线,这显然是错误的。
右旋转后树的结构已经改变,在函数调用需要采用引用传递的方式。
然后来看不采用引用代码怎么写:
int zig(int p) {
int q = a[p].l;
a[p].l = a[q].r, a[q].r = p;
update(p), update(q);
return q;
}
与引用版一样,但返回q,表示新的根节点,这个q可以用来更新它的父节点r的信息。
在调用时:
p = zig(p);
类似的,insert和remove等操作,改变了树的结构,因此需要将信息回溯给上层节点:
root = insert(root, x);
root = removeNode(root, x);
引用版
AcWing 253、平衡树代码
#include <iostream>
using namespace std;
const int N = 100010, INF = 1e8;
struct Node {
int l, r, cnt, sz, val, dat;
} a[N];
int tot, root, n;
int createNode(int val) {
a[++tot].val = val;
a[tot].dat = rand();
a[tot].sz = a[tot].cnt = 1;
return tot;
}
void update(int u) {
a[u].sz = a[a[u].l].sz + a[a[u].r].sz + a[u].cnt;
}
void build() {
createNode(-INF), createNode(INF);
a[1].r = 2, root = 1;
update(root);
}
void zig(int &p) {
int q = a[p].l;
a[p].l = a[q].r, a[q].r = p, p = q;
update(a[p].r), update(p);
}
void zag(int &p) {
int q = a[p].r;
a[p].r = a[q].l, a[q].l = p, p = q;
update(a[p].l), update(p);
}
int getRankByVal(int p, int val) {
if (!p) return 0;
if (a[p].val == val) return a[a[p].l].sz + 1;
if (val < a[p].val) return getRankByVal(a[p].l, val);
else return getRankByVal(a[p].r, val) + a[a[p].l].sz + a[p].cnt;
}
int getValByRank(int p, int rank) {
if (!p) return INF;
if (a[a[p].l]. sz >= rank) return getValByRank(a[p].l, rank);
if (a[a[p].l].sz + a[p].cnt >= rank) return a[p].val;
return getValByRank(a[p].r, rank - a[a[p].l].sz - a[p].cnt);
}
void insert(int &p, int val) {
if (!p) {
p = createNode(val);
return;
}
if (a[p].val == val) {
a[p].cnt++, update(p);
return;
}
if (val < a[p].val) {
insert(a[p].l, val);
if (a[a[p].l].dat > a[p].dat) zig(p);
} else {
insert(a[p].r, val);
if (a[a[p].r].dat > a[p].dat) zag(p);
}
update(p);
}
int getPrev(int val) {
int ans = 1;
int p = root;
while (p) {
if (a[p].val == val) {
if (a[p].l) {
p = a[p].l;
while (a[p].r) p = a[p].r;
ans = p;
}
break;
}
if (a[p].val > a[ans].val && a[p].val < val) ans = p;
p = val < a[p].val ? a[p].l : a[p].r;
}
return a[ans].val;
}
int getNext(int val) {
int ans = 2;
int p = root;
while (p) {
if (a[p].val == val) {
if (a[p].r) {
p = a[p].r;
while (a[p].l) p = a[p].l;
ans = p;
}
break;
}
if (a[p].val < a[ans].val && a[p].val > val) ans = p;
p = val < a[p].val ? a[p].l : a[p].r;
}
return a[ans].val;
}
void removeNode(int &p, int val) {
if (p == 0) return;
if (a[p].val == val) {
if (a[p].cnt > 1) {
a[p].cnt--;
update(p);
return;
}
if (a[p].l || a[p].r) {
if (a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat)
zig(p), removeNode(a[p].r, val);
else
zag(p), removeNode(a[p].l, val);
update(p);
}
else p = 0;
return;
}
val < a[p].val ? removeNode(a[p].l, val) : removeNode(a[p].r, val);
update(p);
}
int main() {
build();
cin >> n;
while (n--) {
int opt, x;
scanf("%d%d", &opt, &x);
switch (opt) {
case 1:
insert(root, x);
break;
case 2:
removeNode(root, x);
break;
case 3:
printf("%d\n", getRankByVal(root, x) - 1);
break;
case 4:
printf("%d\n", getValByRank(root, x + 1));
break;
case 5:
printf("%d\n", getPrev(x));
break;
case 6:
printf("%d\n", getNext(x));
break;
}
}
return 0;
}
非引用版
#include <iostream>
using namespace std;
const int N = 100010, INF = 1e8;
struct Node {
int l, r, cnt, sz, val, dat;
} a[N];
int tot, root, n;
int createNode(int val) {
a[++tot].val = val;
a[tot].dat = rand();
a[tot].sz = a[tot].cnt = 1;
return tot;
}
void update(int u) {
a[u].sz = a[a[u].l].sz + a[a[u].r].sz + a[u].cnt;
}
void build() {
createNode(-INF), createNode(INF);
a[1].r = 2, root = 1;
update(root);
}
int zig(int p) {
int q = a[p].l;
a[p].l = a[q].r, a[q].r = p;
update(p), update(q);
return q;
}
int zag(int p) {
int q = a[p].r;
a[p].r = a[q].l, a[q].l = p;
update(p), update(q);
return q;
}
int getRankByVal(int p, int val) {
if (!p) return 0;
if (a[p].val == val) return a[a[p].l].sz + 1;
if (val < a[p].val) return getRankByVal(a[p].l, val);
else return getRankByVal(a[p].r, val) + a[a[p].l].sz + a[p].cnt;
}
int getValByRank(int p, int rank) {
if (!p) return INF;
if (a[a[p].l].sz >= rank) return getValByRank(a[p].l, rank);
if (a[a[p].l].sz + a[p].cnt >= rank) return a[p].val;
return getValByRank(a[p].r, rank - a[a[p].l].sz - a[p].cnt);
}
int insert(int p, int val) {
if (!p) return createNode(val);
if (a[p].val == val) {
a[p].cnt++, update(p);
return p;
}
if (val < a[p].val) {
a[p].l = insert(a[p].l, val);
if (a[a[p].l].dat > a[p].dat) p = zig(p);
} else {
a[p].r = insert(a[p].r, val);
if (a[a[p].r].dat > a[p].dat) p = zag(p);
}
update(p);
return p;
}
int getPrev(int val) {
int ans = 1;
int p = root;
while (p) {
if (a[p].val == val) {
if (a[p].l) {
p = a[p].l;
while (a[p].r) p = a[p].r;
ans = p;
}
break;
}
if (a[p].val > a[ans].val && a[p].val < val) ans = p;
p = val < a[p].val ? a[p].l : a[p].r;
}
return a[ans].val;
}
int getNext(int val) {
int ans = 2;
int p = root;
while (p) {
if (a[p].val == val) {
if (a[p].r) {
p = a[p].r;
while (a[p].l) p = a[p].l;
ans = p;
}
break;
}
if (a[p].val < a[ans].val && a[p].val > val) ans = p;
p = val < a[p].val ? a[p].l : a[p].r;
}
return a[ans].val;
}
int removeNode(int p, int val) {
if (p == 0) return p;
if (a[p].val == val) {
if (a[p].cnt > 1) {
a[p].cnt--;
update(p);
return p;
}
if (a[p].l || a[p].r) {
if (a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat)
p = zig(p), a[p].r = removeNode(a[p].r, val);
else
p = zag(p), a[p].l = removeNode(a[p].l, val);
update(p);
} else p = 0;
return p;
}
val < a[p].val ? a[p].l = removeNode(a[p].l, val) : a[p].r = removeNode(a[p].r, val);
update(p);
return p;
}
int main() {
build();
cin >> n;
while (n--) {
int opt, x;
scanf("%d%d", &opt, &x);
switch (opt) {
case 1:
root = insert(root, x);
break;
case 2:
root = removeNode(root, x);
break;
case 3:
printf("%d\n", getRankByVal(root, x) - 1);
break;
case 4:
printf("%d\n", getValByRank(root, x + 1));
break;
case 5:
printf("%d\n", getPrev(x));
break;
case 6:
printf("%d\n", getNext(x));
break;
}
}
return 0;
}

