引例：树的查询

题目大意：
现在有一棵树，共有 $n（n \leqslant 10000）$个结点，由 $1 \sim n$ 编号，有 $n- 1$ 条边。现要你完成一些指令，包括：

• $C \ i \ v$：将第 $i$ 条边的权值改为 $v$；
• $Q \ a \ b$：输出结点 $a$ 到结点 $b$ 路径上的最大边权。

首先考虑直接暴力模拟，那么修改是 $O(1)$ 的复杂度，而查询是 $O(n)$的
联想到如果是一维数组的区间最大值的查询修改，也是这个复杂度
但是一维数组可以使用线段树优化，使查询修改的复杂度都变成 $O(\log n)$
问题是在树上如何使用线段树呢

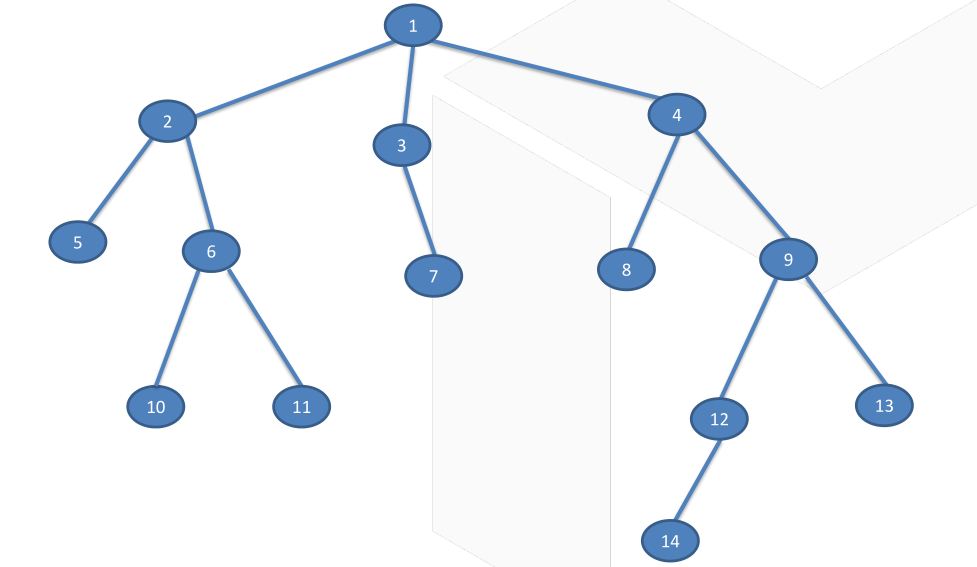
如何在这样一棵树上使用线段树？

退化成链的树

问题简化，可以当做一维数组来处理

树链剖分

当树退化成链时，问题会简化很多
那么可以把树拆成一条条的链！
没错！这就是树链剖分！
看字面意思就能明白，树 $\xrightarrow{\text{剖分}}$ 链

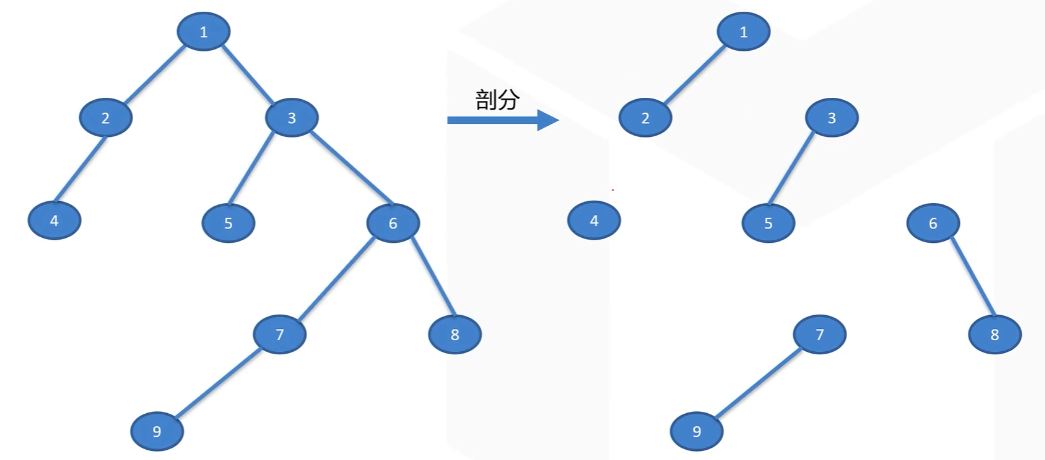
但，这似乎并没有多大的改进…

考虑最坏情况，则会分出 $\frac{n}{2}$ 个链

显然链数越少，链越长越好

要想链尽可能的长，可以把刚才那些散着的链换成附近其他链，以让链连在一起

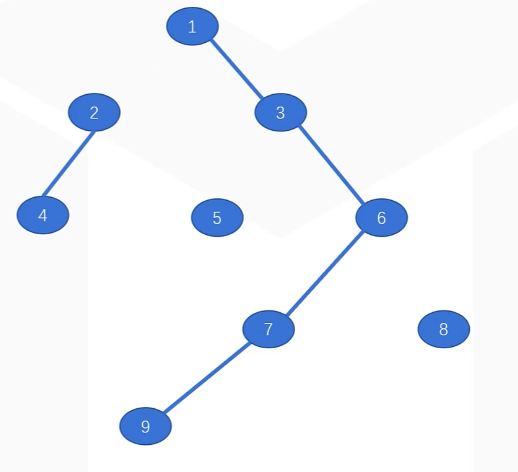
就像这样

得到了一个更好的方案

观察可以发现，改变后剖出来的每条边都是从父节点到后代数最多的那个节点

这样就得到了基于子树结点数的划分方案

轻重边路径剖分：
我们称前面留下来的为重边，删掉的为轻边。一系列相连的重边组成重路径。假设我们剖分的是有根树（没根的随便选个就好了），记 $size(u)$ 为以 $u$ 为根的子树的大小（结点数），那么将每个结点到 $size$ 最大的子结点的边划为重边，其他都是轻边，那个结点称作重儿子。这样就剖分完毕了。

这里暂且先不讨论时间复杂度

树链剖分的组成：

1. $DFS1$: 处理各种信息
2. $DFS2$: 拉重路径
3. 操作转化到数据结构上维护

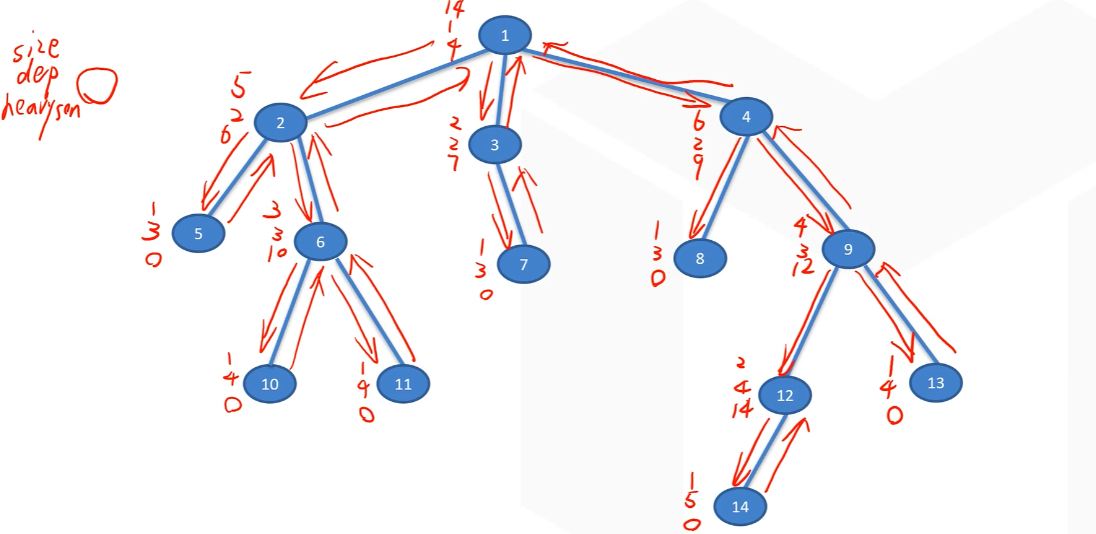
树链剖分——DFS1

• 求出各子树树的大小
• 求出树的深度
• 记录下父亲节点
• 找到重儿子

参考代码：

void dfs1(Node *u) {
    cout << "DFS1\n";
    u->size = 1；
    // 遍历每一个儿子 
    for (Edge *e = u -> head; e != NULL; e = e->next) {
        if (e->to != u->fa) {
            e->to->fa = u; // 记下儿子的父亲是当前的这个节点
            e->to->dep = u->dep + 1; // 记录深度
            dfs1(e->to); // 递归搜索
            u->size += e->to->size; // 累加子树大小
            // 判断更新重儿子
            if (u->heavy_son == NULL || e->to->size > u->heavy_son->size)
                u->heavy_son = e->to; 
        }
    } 
}

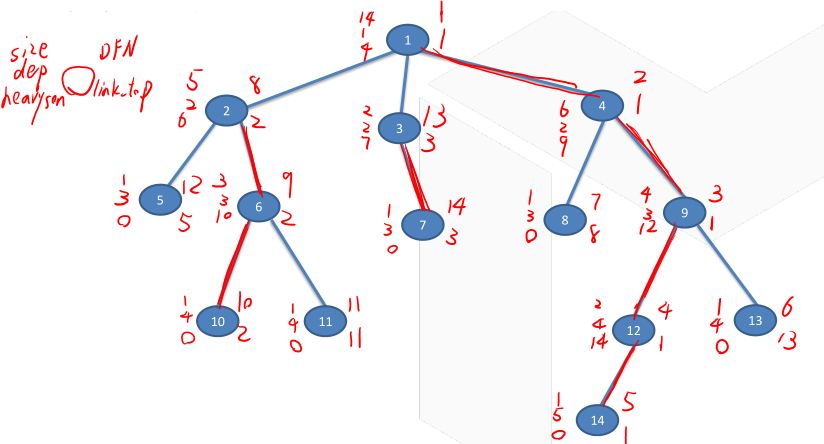
树链剖分——DFS2

• 通过 DFS序 在数据结构中编号
• 将重边拉成链

void dfs2(Node *u) {
    static int DFN = 0; // dfs序
    cout << "DFS2 " << u->dfn;
    Dfn_array[u->dfn = ++DFN] = u->value;   // 记录节点对应的dfs序和dfs序对应的节点
    cout << " " << u->dfn << '\n';
    if (u->link_top == NULL) u-link_top = u; // 如果没有链顶，则把当前的设为链顶
    if (u->heavy_son != NULL) { // 有重儿子 
        u->heavy_son->link->top = u->link_top; 重儿子的链顶是自己的链顶
        dfs(u->heavy_son); // 递归处理 
    } 
    for (Edge *e = u->head; e != NULL; e = e->next) { // 遍历处理其他子树 
        if (e->to != u->fa && e->to != u->heavy_son) 
            dfs(e->to);
    }
}

模拟一遍树链剖分的过程