1维前缀和

定义

给定一个序列 $a[0], a[1], …, a[n-1]$，其前缀和数组 $S$ 定义为 $S[i] = a[0] + a[1] + … + a[i]$。也就是说，$S[i]$ 表示序列中前 $i+1$ 个元素的和。

性质

可以通过计算前缀和数组上两个位置的差值，快速得到原序列中对应区间的和。即，对于任意区间 $[l, r]$，其和可以通过 $S[r] - S[l-1]$ 来计算。由此可以将计算区间和的时间复杂度优化至$O(1)$。
当$l==r$时，$S[r] - S[l-1] = S[r] - S[r-1] = a[r]$。

改进

- 注意到当数组下标从$0$开始时，对于$0$处的求前缀和数组和求区间和都需要特殊处理：
$$\begin{equation} S[i]=\left\{ \begin{aligned} a[0], \quad i=0\\ S[i-1]+a[i], \quad i>0\\ \end{aligned} \right . \end{equation}$$
$$\begin{equation} S[l,r]=\left\{ \begin{aligned} S[r], \quad l=0\\ S[r]-a[l-1], \quad i>0\\ \end{aligned} \right . \end{equation}$$

• 而当数组下标从1开始时,初始化a[0] = 0;S[0] = 0;：
  求前缀和数组：
  $$S[i]=S[i-1]+a[i]$$
  求区间和：
  $$S[l,r]=S[r]+S[l-1]$$

• 所以有关前缀和的题目，为了方便，通常下标都从1开始。

代码

int n, S[1024] = {0};  
cin >> n;  
for (int i = 1; i <= n; ++i) {  
    int a;  
    cin >> a;  
    S[i] = S[i - 1] + a;  
}
int m;  
cin >> m;  
for (int i = 0; i < m; ++i) {  
    int l, r;  
    cin >> l >> r;
    cout << S[r] - S[l - 1] << endl;  
}

2维前缀和

类比于1维前缀和，2维前缀和使用前缀和矩阵$S[m][n]$，每个元素$S[i][j]$存放原矩阵$a[m][n]$中以$(0,0)$为左上角，$(i,j)$为右下角的子矩阵的和。
通常用来求以$(x1,y1)$为左上角，$(x2,y2)$为右下角的任意子矩阵的和。

求法

同样的，下标也从1开始，初始化S[0][j]={0};S[i][0]={0};。
分四部分：
1. 加上其本身$a[i][j]$

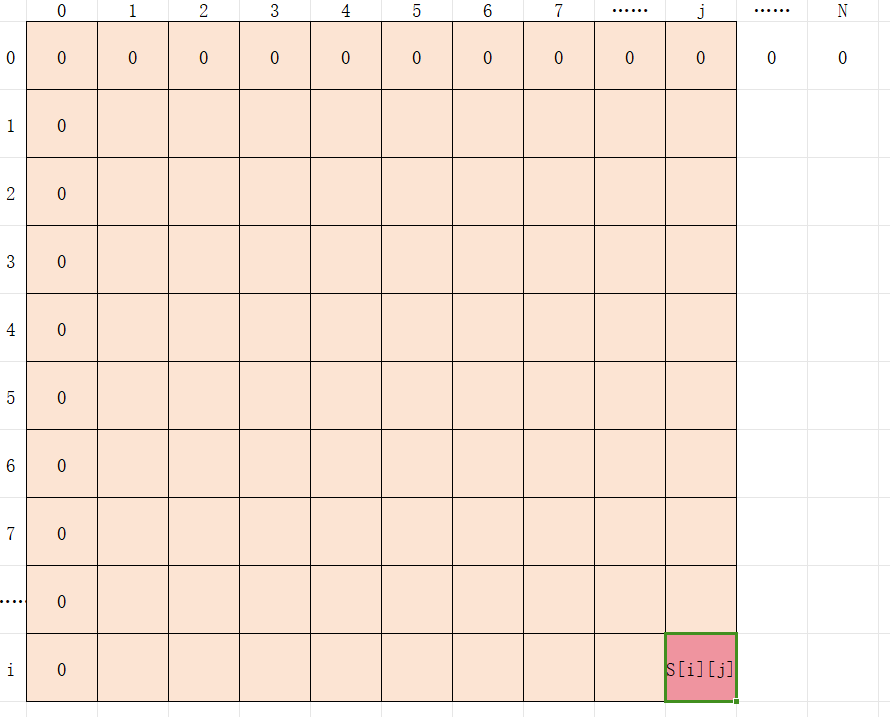
2. 加上它上面的前缀和$S[i-1][j]$

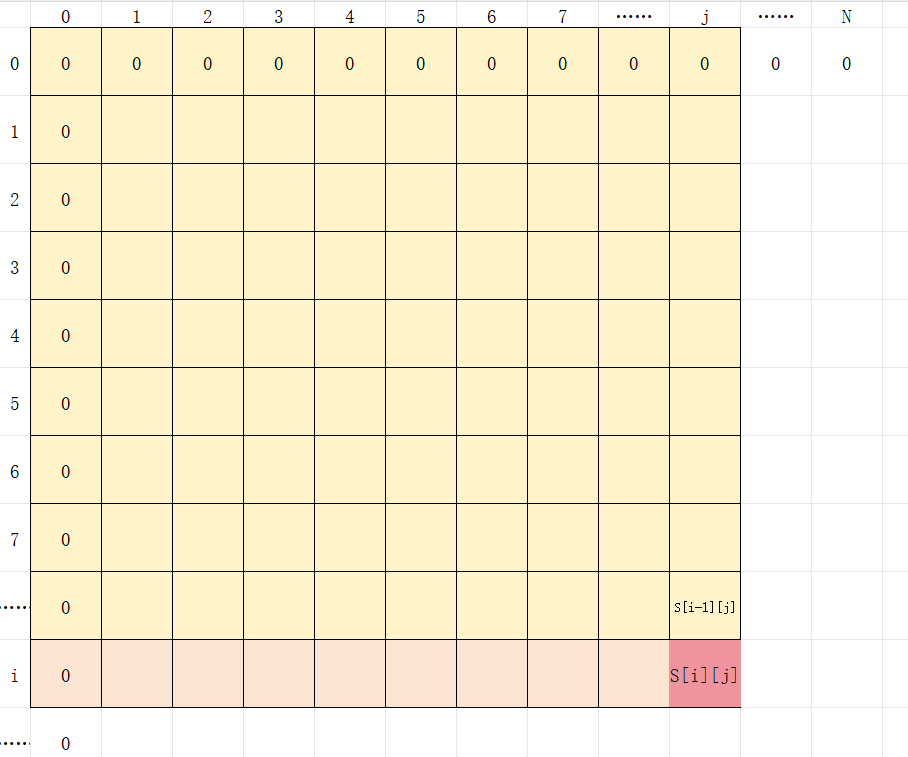
3. 加上它前面的前缀和$S[i][j-1]$

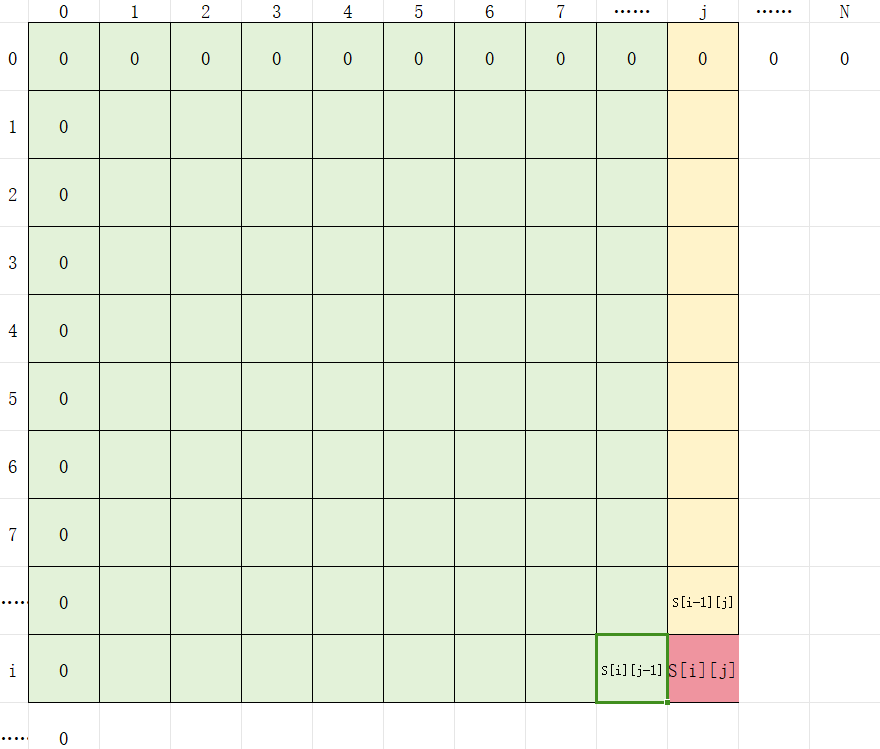
4. 减去重合的部分$S[i-1][j-1]$

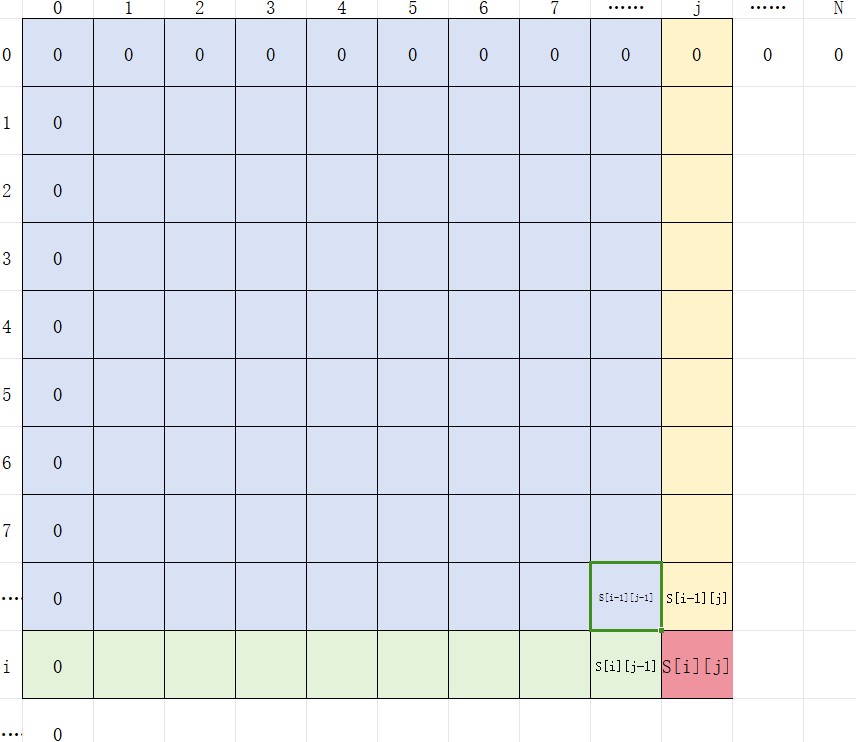
综上：
$$S[i][j] = a[i][j] + S[i-1][j] + S[i][j-1] - S[i-1][j-1]$$

代码

int m, n, S[1024][1024];  
for (int i = 1; i <= m; ++i) {  
    for (int j = 1; j <= n; ++j) {  
        int a;  
        cin >> a;  
        S[i][j] = a + S[i-1][j] + S[i][j-1] - S[i-1][j-1];  
    }  
}

求任意子矩阵和

以$(x1,y1)$为左上角，$(x2,y2)$为右下角
也分4部分：
1. 首先取以$(0,0)$为左上角，$(x2,y2)$为右下角的子矩阵和$S[x2][y2]$

2. 减去子矩阵上面的矩阵和$S[x1-1][y2]$

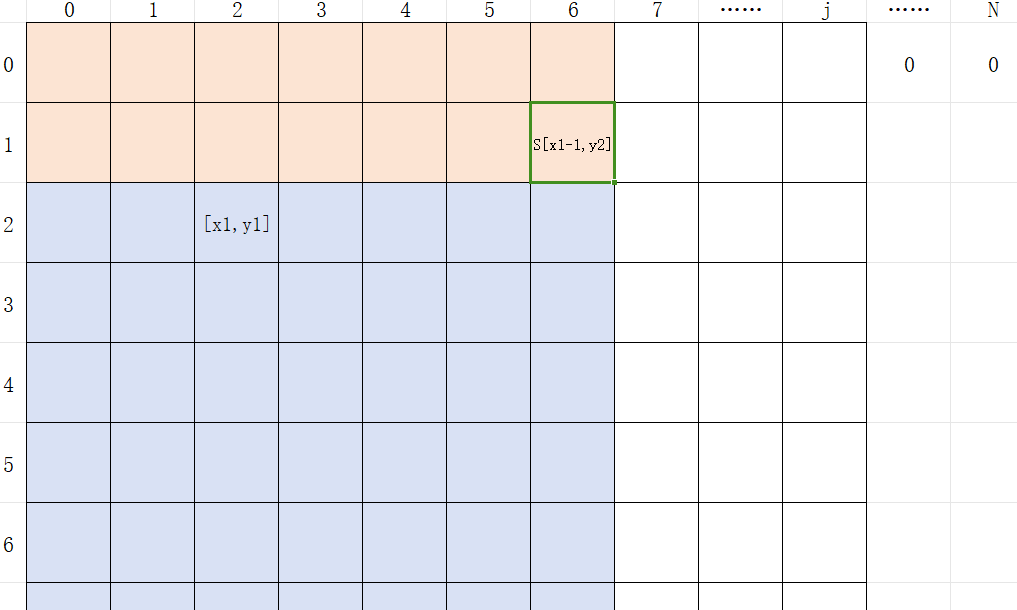
3. 减去子矩阵前面的矩阵和$S[x2][y1-1]$

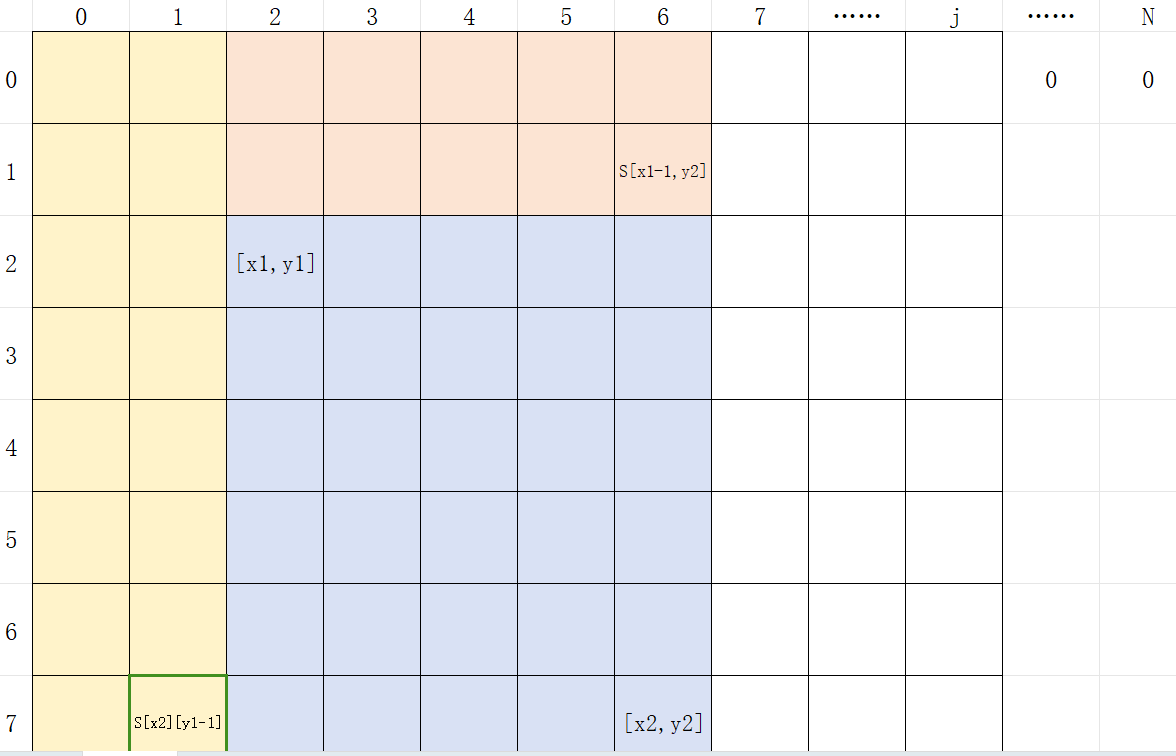
4. 加上重复减去的部分$S[x1-1][y1-1]$

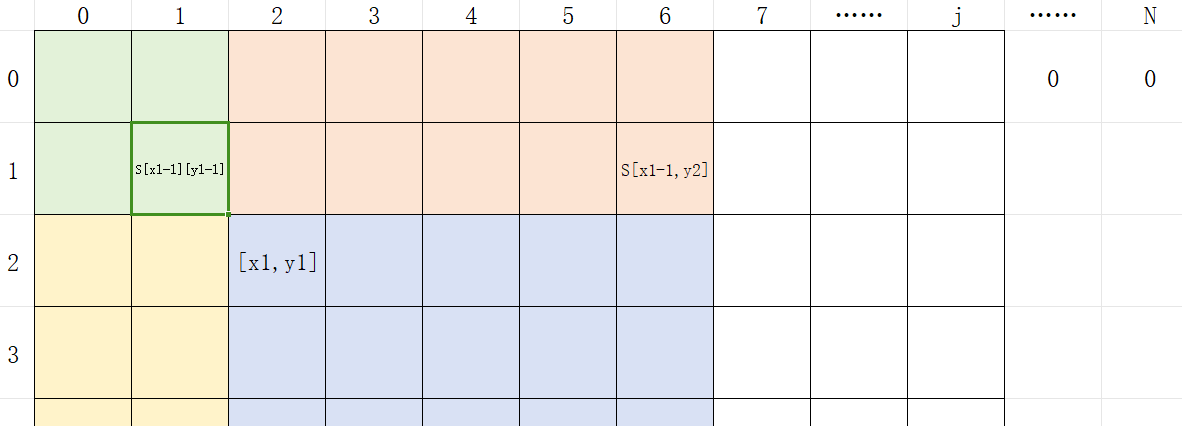
综上：
$$\sum\limits_{i=x1}^{x2}{\sum\limits_{j=y1}^{y2}{a[i][j]}}=S[x2][y2]-S[x1-1][y2]-S[x2][y1-1]+S[x1-1][y1-1]$$

代码

int q, x1, y1, x2, y2;  
for (int i = 0; i < q; ++i) {  
    cin >> x1 >> y1 >> x2 >> y2;  
    cout << S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1] << endl;  
}

1维差分

差分算法可以高效地在一系列数据中执行多次增量操作和查询操作，从而大大减少计算时间。典型的如：多次操作，将序列 $[l,r]$之间的每个数加上$c$，要求输出进行完所有操作后的序列。

算法

1. 构造差分数组int b[N] = {0};
2. 对于每次操作$l,r,c$
   1. 首先b[l]+=c;那么对差分数组求前缀和时，下标$l$之后的元素都会加上$c$
      
   2. 再b[r+1]-=c;修正区间之后的部分，这样求前缀和时，就实现了区间$[l,r]$加$c$
      
   3. 所有操作完成后，对差分数组求前缀和b[i] += b[i-1]，即可得到最终结果

原始数组的输入

有关差分的题目，通常是给出原始数组并在其上面操作
给出长度为$n$的原始序列，第$i$个数$a_i$可以看作对区间$[i,i]$内的每个数加上$a_i$，对应差分数组$b$上的操作即a[i]+=a;a[i+1]-=a;

代码

int n, b[1024];  
cin >> n;  
for (int i = 1; i <= n; ++i) {  
    //输入原始序列  
    int a;  
    cin >> a;  
    b[i] += a;  
    b[i + 1] -= a;  
}  
int m;  
cin >> m;  
for (int i = 0; i < m; ++i) {  
    //进行m次操作  
    int l, r, c;  
    cin >> l >> r >> c;  
    b[l] += c;  
    b[r + 1] -= c;  
}  
for (int i = 1; i <= n; ++i) {  
    //输出最终序列  
    b[i] += b[i - 1];  
    cout << b[i] << " \n"[i == n];  
}

2维差分

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个操作，每个操作包含五个整数 $x_1, y_1, x_2, y_2, c$，其中 $(x_1, y_1)$ 和 $(x_2, y_2)$ 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 $c$。
将完所有操作后的矩阵输出。

算法

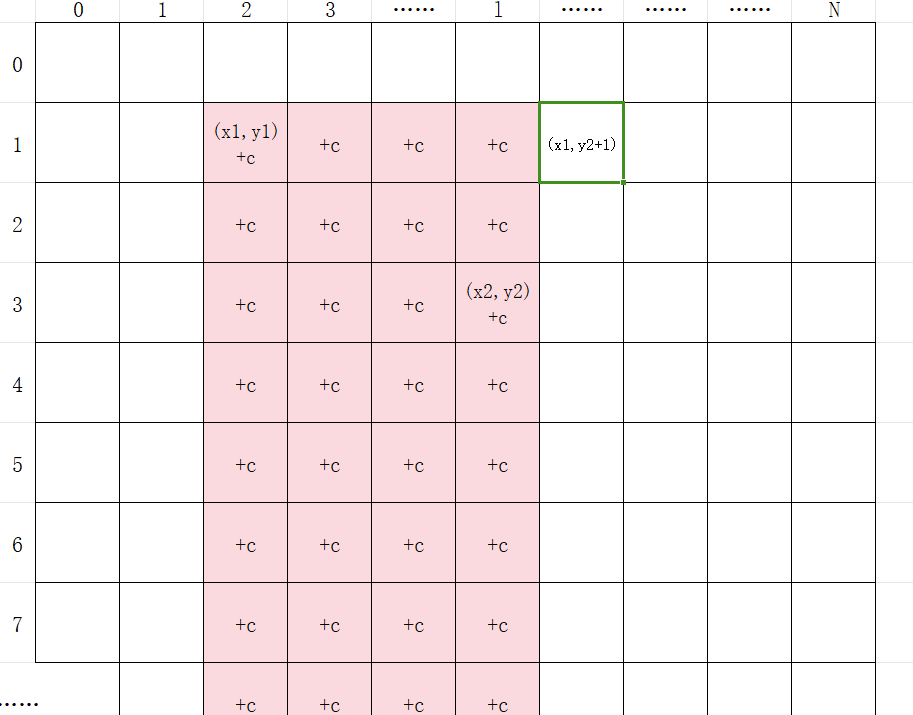
1. 同样的，定义差分数组int b[1024][1024];
2. b[x1][y1]+=c;那么对差分数组求前缀和，所有包含$(x1,y1)$的前缀和都将加上$c$
   
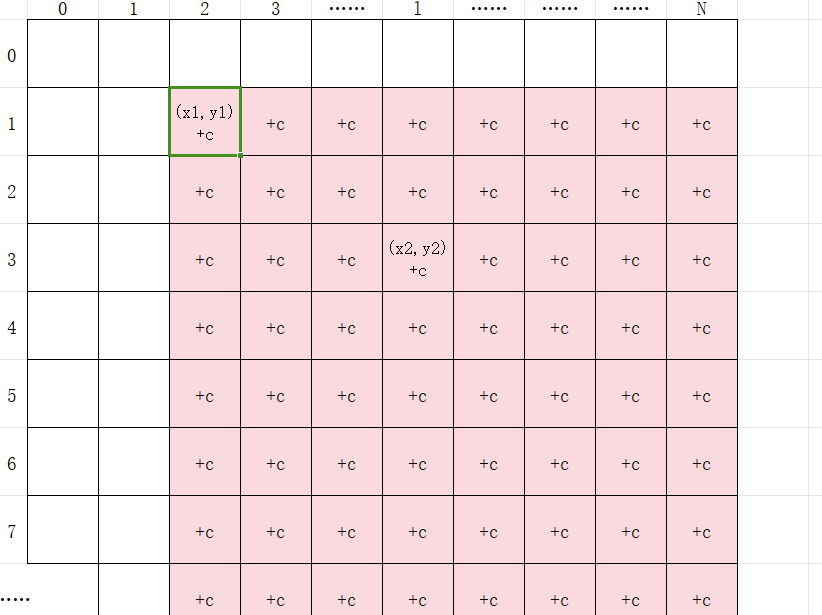
3. b[x1][y2 + 1] -= c;修正指定子矩阵右侧
   
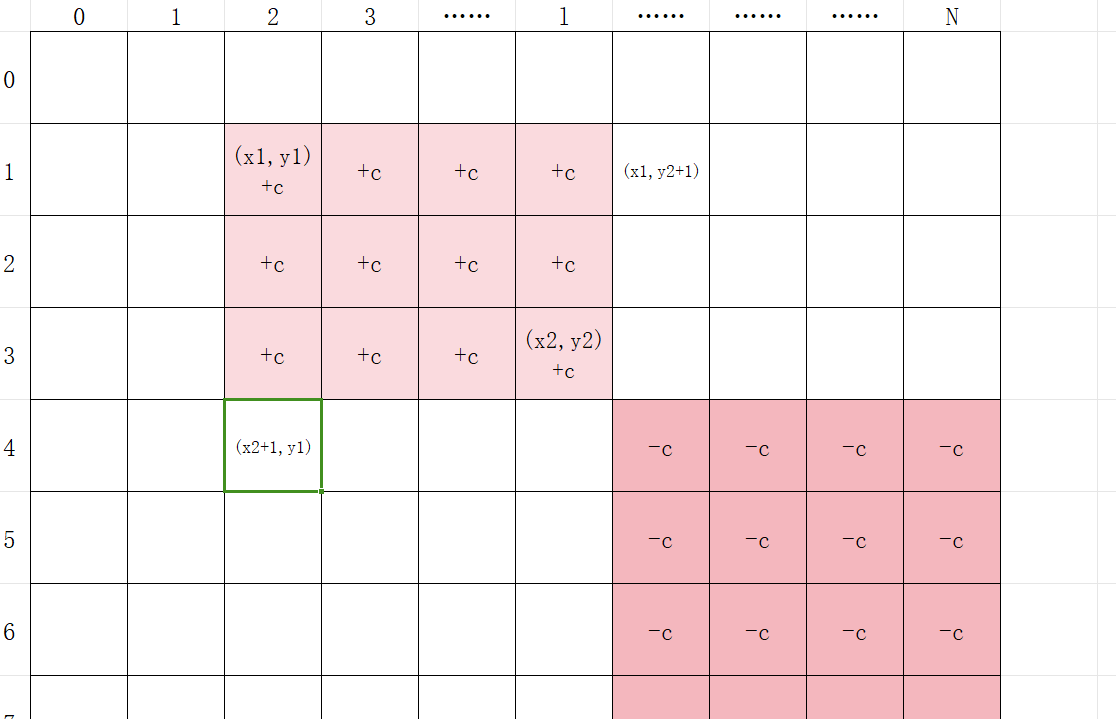
4. b[x2 + 1][y1] -= c;修正指定子矩阵下侧
   
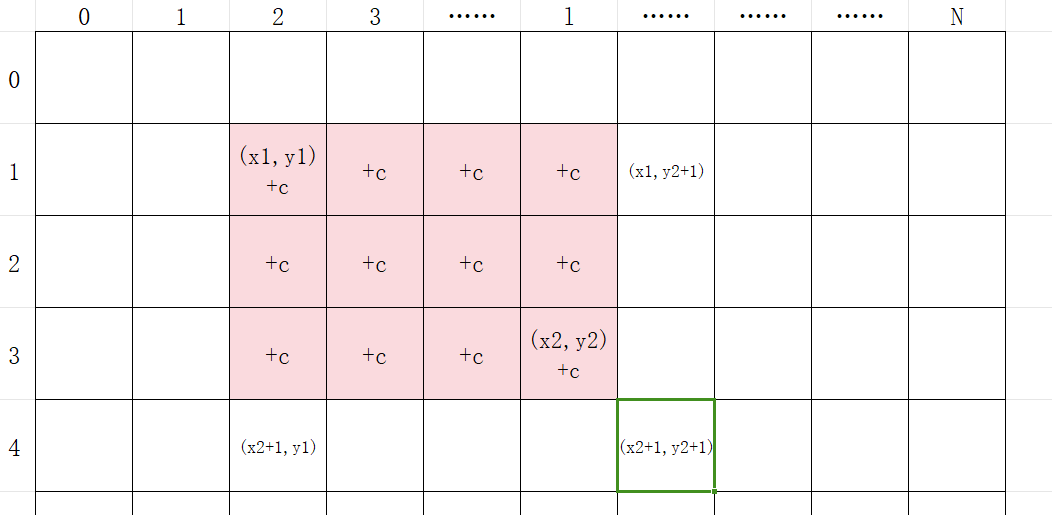
5. b[x2 + 1][y2 + 1] += c;修正右下角重复减去的部分
   
   对于原始数据的输入和1维差分相似，对于原始数据$a[i][j]$对于在差分数组的操作就是以$(i,j)$为左上角，$(i,j)$为右下角的子矩阵内每个元素加$a[i][j]$

代码

AcWing 798. 差分矩阵（算法基础课）

#include <bits/stdc++.h>  

using namespace std;  
//AcWing 798. 差分矩阵（算法基础课）https://www.acwing.com/problem/content/800/  
int b[1024][1024];  

int main() {  
    int n, m, q;  
    cin >> n >> m >> q;  
    for (int i = 1; i <= n; ++i) {  
        for (int j = 1; j <= m; ++j) {  
            int c;  
            cin >> c;  
            //原始数据输入，看成对(i,j)到(i,j)的差分操作  
            b[i][j] += c;//左上角 +            b[i + 1][j] -= c;//左下角 - 修正  
            b[i][j + 1] -= c;//右上角 - 修正  
            b[i + 1][j + 1] += c;//右下角 + 修正  
        }  
    }  
    for (int i = 0; i < q; ++i) {  
        int x1, y1, x2, y2, c;  
        cin >> x1 >> y1 >> x2 >> y2 >> c;  
        //q次操作，二维差分数组  
        b[x1][y1] += c;  
        b[x1][y2 + 1] -= c;  
        b[x2 + 1][y1] -= c;  
        b[x2 + 1][y2 + 1] += c;  
    }  
    for (int i = 1; i <= n; ++i) {  
        for (int j = 1; j <= m; ++j) {  
            //求前缀和得到结果  
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  
            cout << b[i][j] << " \n"[j == m];  
        }  
    }  
    return 0;  
}