什么是倍增

• 倍增是根据已经得到的信息，将考虑的范围扩大一倍，从而加速操作的一种思想。

倍增方法应用之一快速幂代码

\\ a^b%p
#include <iostream>

#define ll long long

int main() {
    int a, b, p, ans = 1;
    std::cin >> a >> b >> p;

    while (b) {
        if (b & 1) ans = (ll)ans * a % p;
        a = (ll)a * a % p;
        b >>= 1;
    }

    std::cout << ans % p << '\n';

    return 0;
}

int fast_pow(int a, int p) {
    int ans = 1;
    for (; p; p >>= 1, a = a * a)
        if (p & 1) 
            ans = ans * a;
    return ans;
}

倍增方法应用之二快速乘思想

计算 $(a * b) \% p$ （a, b均是int64范围内，p是int范围）

解决思路：

• 设 $b$ 的二进制表示为 $b = C_k\*2^k + C_{k - 1}\*2^{k - 1} + + C_0\*2^0$，其中 $C_i \in \{0 \, , 1\}$
• 那么 $a\*b = a\*\left( {\sum\limits_{i = 0}^k {{C_i}\*{2^i}} } \right) = \sum\limits_{i = 0}^k {\left( {a\*{2^i}} \right)}\*{C_i}$
• 由于 $a\*{2^i} = \left( {a\*{2^{i - 1}}} \right)\*2$，而 $C_i$ 可以由 $b \& 1$ 导出，可以进行推导

倍增方法应用之三矩阵快速幂

两个前驱知识需要了解一下
a. 矩阵乘法

• 理解普通矩阵相乘
• 基本性质：满足结合律：$(AB)C=A(BC)$

b. 斐波那契数列作为应用：$f[i] = f[i - 1] + f[i - 2]$，利用矩阵快速幂加快计算速度。

$$\left[ {\begin{array}{*{20}{c}} 0 & 1 \\\ 1 & 1 \\\ \end{array}} \right]\*\left[ {\begin{array}{{20}{c}} {{f_1}} \\\ {{f_2}} \\\ \end{array}} \right] = \left[ {\begin{array}{{20}{c}} {0\*{f_1} + 1\*{f_2}} \\\ {1\*{f_1} + 1\*{f_2}} \\\ \end{array}} \right] = \left[ {\begin{array}{{20}{c}} {{f_2}} \\\ {{f_3}} \\\ \end{array}} \right]$$

$$\left[ {\begin{array}{*{20}{c}} 0 & 1 \\\ 1 & 1 \\\ \end{array}} \right]\*\left[ \begin{array}{l} {f_2} \\\ {f_3} \\\ \end{array} \right] = \left[ \begin{array}{l} 0\*{f_2} + 1\*{f_3} \\\ 1\*{f_2} + 1\*{f_3} \\\ \end{array} \right] = \left[ \begin{array}{l} {f_3} \\\ {f_4} \\\ \end{array} \right]$$

$$\left[\begin{array}{ll} 0 & 1 \\\ 1 & 1 \end{array}\right] \*\left[\begin{array}{ll} 0 & 1 \\\ 1 & 1 \end{array}\right] \*\left[\begin{array}{l} f_{1} \\\ f_{2} \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\\ 1 & 1 \end{array}\right] \*\left[\begin{array}{l} f_{2} \\\ f_{3} \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\\ 1 & 1 \end{array}\right]^{2} \*\left[\begin{array}{l} f_{2} \\\ f_{3} \end{array}\right]=\left[\begin{array}{l} f_{3} \\\ f_{4} \end{array}\right]$$

$${\left[ {\begin{array}{*{20}{c}} 0 & 1 \\\ 1 & 1 \\\ \end{array}} \right]^{n - 1}}\*\left[ \begin{array}{l} {f_1} \\\ {f_2} \\\ \end{array} \right] = \left[ \begin{array}{l} {f_n} \\\ {f_{n + 1}} \\\ \end{array} \right]$$

核心是矩阵倍增

倍增方法应用之四RMQ问题ST表

RMQ问题是一个经典的可以用倍增来解决的问题：

给定一个长度为 $n$ 的序列 $A[1 \cdots n]$，有 $q$ 次询问，每次询问给出 $x \, , y$，回答 $A[x \cdots y]$ 中的最大值。（也可以是最小值，此处以最大值为例）通常 $n, q \leqslant 100000$

首先介绍利用倍增解决RMQ问题的算法：$ST(Sparse \, Table)$算法

一般RMQ问题的ST算法

对于序列 $A[1 \cdots n]$，我们构造一个二维数组 $st[1 \cdots n][0 \cdots \log_2 n]$
$st[i][j]$ 表示从 $i$ 这个位置开始，向后 $2^j$ 个位置（包括 $i$）的最大值，即 $Max\{A[i \cdots i + 2^j - 1]\}$

这里如何构造ST表呢？
这里利用倍增思想

构造数组 $B$，使得 $B[i,j]$ 表示 $A[i \cdots i + 2 ^ j - 1]$ 中最小数的下标。可以在 $O(N\log_2 N)$ 的时间内得到这个数组。然后对于每对 $i\, , j$，令 $k = \left\lfloor {{{\log }_2}\left( {j - i + 1} \right)} \right\rfloor$，则比较 $A[B[i,k]]$ 与 $A[B[j-2^k+1,k]]$ 的大小就可以得到结果了。每次询问时间复杂度为 $O(1)$

显然：$st[i][0] = A[i]$
除此之外，任何一个 $st[i][j]$ 所表示的区间长度都是 $2$ 的整数次方，即 $2^j$
我们将该区间从中间划分为两段，各长 $2^{j-1}$
容易得到，两段区间的起点分别为 $i$ 和 $i + 2 ^ {j - 1}$
于是容易想到：
$st[i][j] = max\{st[i][j-1], st[i + (1 << j - 1)][j-1]\}$
我们先从 $1$ 到 $n$ 枚举 $j$，再顺序枚举 $i$，即可构造 $st$ 数组

for (int i = 1; i <= n; ++i) st[i][0] = A[i];
for (int j = 1; (1 << j) <= n; ++j)
    for (int i = 1; i + (1 << j) - 1 <= n; ++i)
        st[i][j] = max(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);

时间复杂度是 $O(n\log n)$

构造出 $st$ 表后该如何询问呢？

对于每次询问给出的$x \, , y$，其长度 $len=y-x+1$
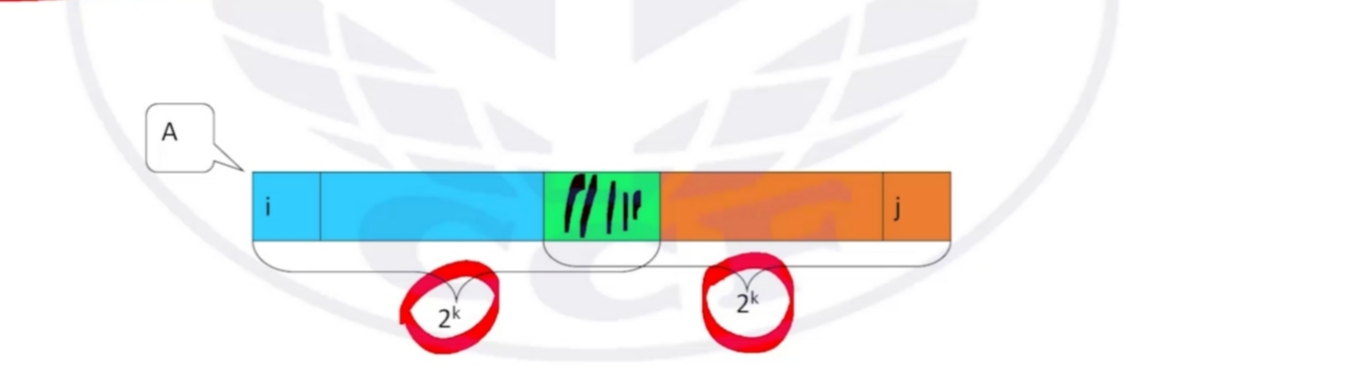
我们先找到最大的且小于等于 $len$ 的 $2$ 的整数次幂，例如是$2^k$
那么 $[x \cdots y]$ 这个区间的前 $2^k$ 和 后 $2^k$ 个位置合起来可以完全覆盖该区间
于是 $Max\{A[x \cdots y]\} = max(st[x][k], st[y - (1 << k) + 1][k])$

$k = \left\lfloor {{{\log }_2}\left( {j - i + 1} \right)} \right\rfloor$

在C++中可写为k=(int)(log(y-x+1) / log2)

int query(int x, int y) {
    int k = (int)(log(y - x + 1) / log(2));
    int m = max(st[x][k], st[y - (1 << k) + 1][k]);
    return m;
}

时间复杂度 $O(1)$

倍增方法应用之五RMQ问题树上最近公共祖先

树上最近公共祖先，简称LCA，是关于树的一个非常基础的概念：
给定一颗有根树，一个点到根节点的路径上的所有点称为该点的祖先。
若点 $u$ 同时是点 $x, y$ 的祖先，那么 $u$ 称为 $x, y$ 的公共祖先。$x,y$ 的所有公共祖先中，深度最大的点称为 $x,y$ 的最近公共祖先。
另一种理解：$x$ 到 $y$ 的路径上深度最小的点为 $x,y$ 的最近公共祖先。

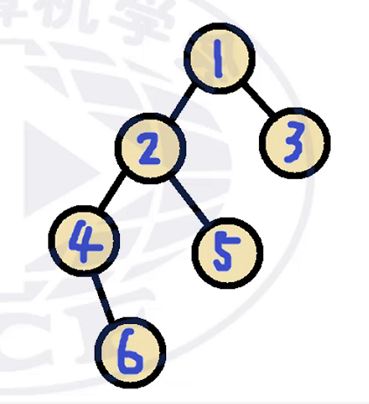
例如在该图中
以 $1$ 为根节点
节点 $5$ 和 $6$ 的最近公共祖先就是节点 $2$
节点 $5$ 和 $1$ 的最近公共祖先就是节点 $1$

在倍增求解LCA的算法中，我们首先需要预处理出每个节点的深度（以 $1$ 为根节点且深度为 $1$）

void dfs(int u, int fa) {
    for (int o = b[u]; o != -1; o = e[o].next) {
        if (e[o].v == fa) continue;
        d[e[o].v] = d[u] + 1;
        dfs(e[o].v, u);
    }
}

int main() {
    d[1] = 1;
    dfs(1, 0);
}

接下来，我们需要构造一个数组 $f[i][j]$，表示节点 $i$ 向上走 $2^j$ 步后到达哪个节点。如何构造该数组呢？

显然：
$f[i][0] = i$ 的父节点
对于 $j \neq 0$，我们可以先向上走 $2 ^ {j-1}$ 步，再向上走 $2 ^ {j - 1}$ 步，其中第一次走 $2 ^ {j - 1}$ 步后到达 $f[i][j - 1]$
于是f[i][j] = f[f[i][j-1]][j-1]

于是dfs可以改为如下形式：

void dfs(int u) {
    for (int i = 1; i <= 16; ++i)
        f[u][i] = f[f[u][i - 1]][i - 1];
    for (int o = b[u]; o != -1; o = e[o].next) {
        if (e[o].v == f[u][0]) continue;
        d[e[o].v] = d[u] + 1;
        f[e[o].v][0] = u;
        dfs(e[o].v, u);
    }
}

int main() {
    d[1] = 1;
    dfs(1);
}

这样我们构造出了 $f[i][j]$
接下来考虑如何求解 $x,y$ 的 LCA

该算法主要分为两步：
1、将 $x,y$ 调整到同一深度
2、求解 $x,y$ 的LCA

我们不妨令 $d[x]>d[y]$（否则$swap(x,y)$），考虑将 $x$ 走到与 $y$ 同一深度
我们当然可以让 $x$ 一步一步向上爬，但是太慢

假设 $x$ 需要向上走 $a$ 步可以与 $y$ 同一深度
我们可以将 $a$ 按照二进制分解
例如 $a=16$，其二进制为 $11010$，即$a=2^4+2^3+2^1$
我们可以让 $x$ 先走 $2^4$ 步，再走 $2^3$ 步，再走 $2^1$ 步与 $y$ 同深度，这一过程可以直接查询 $f[i][j]$ 表

实际上，我们并不需要像快速幂一样将 $a$ 模 $2$ 来获得二进制，我们可以从大到小枚举 $i$，若 $d[f[x][i]] \geq d[y]$，则令 $x = f[x][i]$

if (d[x] < d[y]) swap(x, y);
for (int i = 16; i >= 0; --i)
    if (d[f[x][i]] >= d[y])
        x = f[x][i];

这一步时间复杂度为 $O(\log n)$

在将 $x,y$ 调整到同一深度后，进行求LCA的第二步操作
在此之前，一定注意：若 $x$ 已经与 $y$ 相同，则 $LCA = x$！！！

接下来就是 $x, y$ 深度相同后点不同的情况
对于这种情况，我们每次将 $x,y$ 向上走同样的距离，并使得 $x,y$ 在保持不同的情况下尽量靠上，如此以后，$LCA=f[x][0]$
考虑如何进行这一步操作

例题1：Doubling

在 $N$ 个洞的沙坑中住着一只蚂蚁。这只蚂蚁的动作很有规律，在进入洞 $i$ 的第 $2$ 天就会移动到洞 $A_i$。
关于那个，请处理以下 $Q$ 个询问：

• 第 $j$ 个询问：如果蚂蚁当前在洞 $X_j$，$Y_j$ 天后在哪个洞？

限制：

• $1 \leqslant N, Q \leqslant 10^5$
• $1 \leqslant A_i, X_j \leqslant N$
• $1 \leqslant Y_j \leqslant 10^9$

算法分析

记 dp[d][x] 表示蚂蚁当前在洞 $x$ 时，在经过 $2^d$ 天后进入哪个洞

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n, q;
    cin >> n >> q;

    vector<int> a(n);
    rep(i, n) cin >> a[i];
    rep(i, n) a[i]--;

    const int D = 30;
    vector dp(D, vector<int>(n));
    rep(d, D)rep(i, n) {
        if (d == 0) dp[d][i] = a[i];
        else dp[d][i] = dp[d-1][dp[d-1][i]];
    }

    rep(qi, q) {
        int x, y;
        cin >> x >> y;
        --x;
        int ans = x;
        rep(d, D) if (y>>d&1) ans = dp[d][ans];
        ++ans;
        cout << ans << '\n';
    }

    return 0;
}

例题2：Calculator

对于 $1, 2, \cdots, N$ 中的每个数，求出执行以下操作 $K$ 次后得到的整数。

• 用自身减去它在十进制表示下的每一位上的数

限制：

• $1 \leqslant N \leqslant 3 \times 3 \times 10^5$
• $1 \leqslant K \leqslant 10^9$

算法分析

记 dp[d][x] 表示对 $x$ 执行 $2^d$ 次操作后得到的整数

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n, k;
    cin >> n >> k;

    const int D = 30;
    vector dp(D, vector<int>(n+1));
    for (int i = 1; i <= n; ++i) {
        string s = to_string(i);
        int now = i;
        for (char c : s) {
            now -= c-'0';
        }
        dp[0][i] = now;
    }
    for (int d = 1; d < D; ++d) {
        for (int i = 1; i <= n; ++i) {
            dp[d][i] = dp[d-1][dp[d-1][i]];
        }
    }

    for (int i = 1; i <= n; ++i) {
        int ans = i;
        rep(d, D) if (k>>d&1) ans = dp[d][ans];
        cout << ans << '\n';
    }

    return 0;
}