本文只讲模式串p的ne数组
ne[i]的定义：以i结尾的最长相同前缀后缀。
i为当前量，假设ne[1~i-1]已经求出，现在求解ne[i]。这时典型dp的思想，截取一个单元分析。
完整代码：

#include <cstdio>
#include <cstring>
using namespace std;
const int N=100;
char p[N];
int ne[N];
int main(){
    scanf("%s",p+1);
    int n=strlen(p+1);
    for(int i=2,j=0;i<=n;i++){
        while(j>0 && p[i]!=p[j+1]) j=ne[j];
        if(p[i]==p[j+1]) j++;
        ne[i]=j;
        printf("%d ",j);
    } 
    return 0;
}

样例输入输出：

aacdaad
1 0 0 1 2 0

讲解：
第一点：
while(j && p[i]!=p[j+1]) j=ne[j];

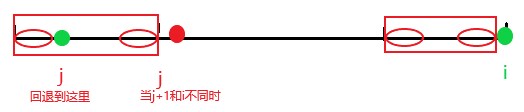
如果j+1不能和i匹配，这时研究以j结尾的字符串，正好和ne[j]的定义相呼应。
如果j+1和i匹配失败，j回退到上一个匹配成功的地方，也就是ne[j].

第二点：
if(p[i]==p[j+1]) j++;
如果找到匹配，j加1

第三点：
ne[i]=j;
j的值就是以i结尾最长的相同前后缀的字符个数。

难点感悟：
每一次回退，也是一次比较，利用了已知结果。
证明式跳跃思维是理解的关键。不要陷入回退的漩涡，而是简单证明它。
一直回退必到0的证明：
ne[i]为以i结尾的最长前后缀，故i结尾的字符串，ne[i]最大值为i-1，假设字符串从1开始编号。
那么j=ne[j]能获得的最大值是j-1,故这是一个单调递减的过程。
所以一直回退肯定到0.
证明完毕。