主席树笔记
前言
打模拟赛的时候,不会主席树,暴毙;
打ACM的时候,不会主席树,暴毙;
现在终于断断续续地学会了,发笔记以记之。
(我终于一雪前耻了)
静态区间第 k 小问题
题意
给出一个序列,每次询问给定区间内第k小的值。
思路
主席树模板。
考虑最简单的情况,也就是查询区间固定。首先对数据进行离散化,用线段树维护。每个节点对应离散化后值域的数的总个数 size.从上到下进行查询时,判断当前节点左子树的 $size$ 和排名 $k$ 的关系,如果是小于等于就到左子树里面去,否则到右子树中查找 $k-size$ (这个原理参考平衡树的kth)。
如何维护所有区间?最直接的想法就是建 $N$ 个线段树,维护 $[i,i]$ 的区间情况,利用前缀和实现所有区间。但空间肯定会炸。
考虑可持久化线段树是如何解决空间问题的。显然,从区间 $[1,i-1]$ 到 $[1,i]$ 只是改变了一个值,那么同样的,每增加一个区间只需要新开 $logn$ 个节点即可。
图解如下。
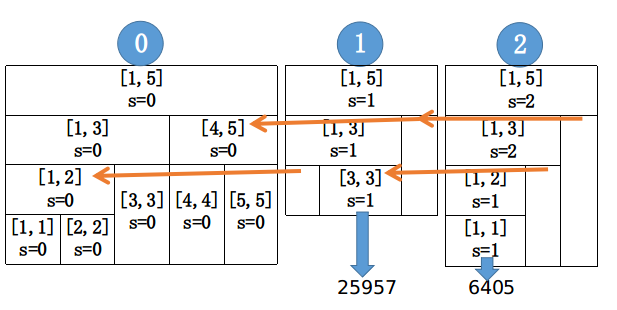
//P3834 【模板】可持久化线段树 2(主席树)
//每一棵线段树维护一个区间的最值,然后按照可持久化的思想,每一棵新的树增加log个节点。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+10;
struct node
{
int l,r,sum;
}tr[N<<5];
int a[N],rt[N],n,m,tot=0;
vector<int> v;
int getid( int k )
{
return lower_bound( v.begin(),v.end(),k )-v.begin()+1;
}
void build( int &trt,int l,int r )
{
trt=++tot; tr[trt].sum=0;
if ( l==r ) return;
int mid=(l+r)>>1;
build( tr[trt].l,l,mid ); build( tr[trt].r,mid+1,r );
}
void update( int l,int r,int &now,int las,int k )
{
tr[++tot]=tr[las];
now=tot; tr[tot].sum++;
if ( l==r ) return;
int mid=(l+r)>>1;
if ( k<=mid ) update( l,mid,tr[now].l,tr[las].l,k );
else update( mid+1,r,tr[now].r,tr[las].r,k );
}
int query( int l,int r,int x,int y,int k )
{
if ( l==r ) return l;
int mid=(l+r)>>1,cnt=tr[tr[y].l].sum-tr[tr[x].l].sum;
if ( cnt>=k ) return query( l,mid,tr[x].l,tr[y].l,k );
else return query( mid+1,r,tr[x].r,tr[y].r,k-cnt );
}
int main()
{
scanf( "%d%d",&n,&m );
for ( int i=1; i<=n; i++ )
scanf( "%d",&a[i] ),v.push_back( a[i] );
sort( v.begin(),v.end() );
v.erase( unique(v.begin(),v.end()),v.end() );
build( rt[0],1,n );
for ( int i=1; i<=n; i++ )
update( 1,n,rt[i],rt[i-1],getid(a[i]) );
while ( m-- )
{
int l,r,k; scanf( "%d%d%d",&l,&r,&k );
printf( "%d\n",v[query(1,n,rt[l-1],rt[r],k)-1] );
}
}
动态区间第 k 小问题
题意
给定一个含有 $n$ 个数的序列 $a_1,a_2 \dots a_n$ ,需要支持两种操作:
Q l r k表示查询下标在区间 $[l,r]$ 中的第 $k$ 小的数C x y表示将 $a_x$ 改为 $y$
思路
把树状数组套在线段树上,每个树状数组的节点为一个线段树根节点,利用树状数组来维护前缀和。
对于修改操作,设位置为 $i$,从下标为 $i$ 的树状数组节点开始,每次往后跳,所有跳到的线段树都改一遍,原值对应区间-1,新值对应区间+1。一共要改 $log$ 棵树。
对于查询操作,先把 $l−1$ 和 $r$ 都往前跳,每次跳到的都记下来。求当前 $size$ 的时候,用记下来的 $log$ 棵由 $r$ 得到的节点左儿子的 $size$ 和(就代表 $[1,r]$ 的 $size$ )减去 $log$ 棵由 $l−1$ 得到的节点左儿子的 $size$ 和(就代表 $[1,l−1]$ 的$size$ )就是 $[l,r]$ 的 $size$ 。往左/右儿子跳的时候也是 $log$ 个节点一起跳。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct SegmentTree
{
int val,l,r;
}tr[N*400];
struct Question
{
bool typ; int l,r,k,pos,t;
}q[N];
int n,m,a[N],rt[N],len,tot,tmp[2][20],cnt[2],num[N<<1];
char opt[10];
int lowbit( int x ) { return x&(-x); }
void modify( int &p,int l,int r,int pos,int val )
{
if ( !p ) p=++tot;
tr[p].val+=val;
if ( l==r ) return;
int mid=(l+r)>>1;
if ( pos<=mid ) modify( tr[p].l,l,mid,pos,val );
else modify( tr[p].r,mid+1,r,pos,val );
}
void init_modify( int x,int val )
{
int k=lower_bound( num+1,num+len+1,a[x] )-num;
for ( int i=x; i<=n; i+=lowbit(i) )
modify( rt[i],1,len,k,val );
}
int query( int l,int r,int k )
{
if ( l==r ) return l;
int mid=(l+r)>>1,sum=0;
for ( int i=1; i<=cnt[1]; i++ )
sum+=tr[tr[tmp[1][i]].l].val;
for ( int i=1; i<=cnt[0]; i++ )
sum-=tr[tr[tmp[0][i]].l].val;
if ( k<=sum )
{
for ( int i=1; i<=cnt[1]; i++ )
tmp[1][i]=tr[tmp[1][i]].l;
for ( int i=1; i<=cnt[0]; i++ )
tmp[0][i]=tr[tmp[0][i]].l;
return query( l,mid,k );
}
else
{
for ( int i=1; i<=cnt[1]; i++ )
tmp[1][i]=tr[tmp[1][i]].r;
for ( int i=1; i<=cnt[0]; i++ )
tmp[0][i]=tr[tmp[0][i]].r;
return query( mid+1,r,k-sum );
}
}
int init_query( int l,int r,int k )
{
memset( tmp,0,sizeof(tmp) );
cnt[0]=cnt[1]=0;
for ( int i=r; i; i-=lowbit(i) )
tmp[1][++cnt[1]]=rt[i];
for ( int i=l-1; i; i-=lowbit(i) )
tmp[0][++cnt[0]]=rt[i];
return query( 1,len,k );
}
int main()
{
scanf( "%d%d",&n,&m );
for ( int i=1; i<=n; i++ )
scanf( "%d",&a[i] ),num[++len]=a[i];
for ( int i=1; i<=m; i++ )
{
scanf( "%s",opt );
q[i].typ=(opt[0]=='Q');
if ( q[i].typ ) scanf( "%d%d%d",&q[i].l,&q[i].r,&q[i].k );
else scanf( "%d%d",&q[i].pos,&q[i].t ),num[++len]=q[i].t;
}
//printf( "input has done." );
sort( num+1,num+1+len ); len=unique( num+1,num+1+len )-num-1;
for ( int i=1; i<=n; i++ )
init_modify( i,1 );
for ( int i=1; i<=m; i++ )
if ( q[i].typ ) printf( "%d\n",num[init_query(q[i].l,q[i].r,q[i].k)] );
else
{
init_modify( q[i].pos,-1 ); a[q[i].pos]=q[i].t; init_modify( q[i].pos,1 );
}
}
树上路径第 k 小问题
题意
给定一棵 $n$ 个节点的树,每个点有一个权值。有 $m$ 个询问,每次给你 $u,v,k$ ,你需要回答 $u \text{ xor last}$ 和 $v$ 这两个节点间第 $k$ 小的点权。其中 $\text{last}$ 是上一个询问的答案,定义其初始为 $0$ ,即第一个询问的 $u$ 是明文。
思路
显然,首先可以树上差分维护每个点到根的前缀和。
询问 $u,v$ 的时候,可以知道 $siz[rt,u]$ 和 $siz[rt,v]$ 的和。那么,用 $siz[rt,u]+siz[rt,v]-siz[rt,lca]-siz[rt,fa[lca]]$ ,四个点一起跳。每个点对应的线段树从其父亲的线段树继承而来(根节点从 $0$ 号空线段树继承而来),这两个操作在 dfs 建树时就可以一并处理。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=2e6+10;
struct edge
{
int to,nxt;
}e[N<<1];
int n,m,s,lasans=0,tot,cnt,head[N];
int a[N],tmp[N],fa[N][35],dep[N],rt[M]={0},ls[M]={0},rs[M]={0},siz[M]={0};
void add( int u,int v )
{
e[++tot]=(edge){v,head[u]}; head[u]=tot;
}
void modify( int &rt,int las,int l,int r,int val )
{
if ( !rt ) rt=++cnt;
if ( l==r ) { siz[rt]++; return; }
int mid=(l+r)>>1;
if ( mid>=val ) modify( ls[rt],ls[las],l,mid,val ),rs[rt]=rs[las];
else modify( rs[rt],rs[las],mid+1,r,val ),ls[rt]=ls[las];
siz[rt]=siz[ls[rt]]+siz[rs[rt]];
}
int query( int rt1,int rt2,int rt3,int rt4,int l,int r,int k )
{
if ( l==r ) return l;
int mid=(l+r)>>1,tmp=siz[ls[rt1]]+siz[ls[rt2]]-siz[ls[rt3]]-siz[ls[rt4]];
if ( tmp>=k ) return query( ls[rt1],ls[rt2],ls[rt3],ls[rt4],l,mid,k );
else return query( rs[rt1],rs[rt2],rs[rt3],rs[rt4],mid+1,r,k-tmp );
}
void dfs( int u,int fat )
{
dep[u]=dep[fat]+1;
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to;
if ( v==fa[u][0] ) continue;
fa[v][0]=u; modify( rt[v],rt[u],1,s,a[v] ); dfs( v,u );
}
}
int lca( int x,int y )
{
if ( dep[x]<dep[y] ) swap( x,y );
int del=dep[x]-dep[y];
for ( int i=0; (1<<i)<=del; i++ )
if ( (1<<i)&del ) x=fa[x][i];
for ( int i=20; i>=0; i-- )
if ( fa[x][i] != fa[y][i] ) x=fa[x][i],y=fa[y][i];
return x==y ? x : fa[x][0];
}
int main()
{
scanf( "%d%d",&n,&m );
for ( int i=1; i<=n; i++ )
scanf( "%d",&tmp[i] ),a[i]=tmp[i];
//----------------input-----------------
sort( tmp+1,tmp+1+n ); s=unique( tmp+1,tmp+1+n )-tmp;
for ( int i=1,u,v; i<n; i++ )
scanf( "%d%d",&u,&v ),add( u,v ),add( v,u );
for ( int i=1; i<=n; i++ )
a[i]=lower_bound( tmp+1,tmp+1+s,a[i] )-tmp;
//--------------离散化-------------------
modify( rt[1],rt[0],1,s,a[1] ); dfs( 1,0 ); int lim=log2(n);
for ( int k=1; k<=lim; k++ )
for ( int i=1; i<=n; i++ )
fa[i][k]=fa[fa[i][k-1]][k-1];
//-------------prework------------------
while ( m-- )
{
int u,v,k; scanf( "%d%d%d",&u,&v,&k );
u^=lasans;
int _lca=lca(u,v),ans=tmp[query(rt[u],rt[v],rt[_lca],rt[fa[_lca][0]],1,s,k)];
printf( "%d\n",ans ); lasans=ans;
}
}


ACM和那些高中或以下竞赛都是一个类型的OJ题是么?也就是说必须编程能力很强才能参赛么,还是说其他系如数学也能报着玩
ACM和你所说的竞赛都是偏算法偏思维的,要求确实很高;但是一般而言数学好的人学起来都超级快,把一开始就纯信息竞赛的人吊起来打(
然后 ACM 和 NOIP 内容其实差不多,但是两个赛制不一样,对能力要求也就有所不同。
ACM组队,配合也挺重要的;OI赛制的话一个人打,能力肯定要全面;而且ACM能实时查看结果,OI赛制的话就以最终结果为准,中途是不能提交的,只能靠自己造数据和下发的样例
我这样的话主要还是NOIP为主,那个ACM是机房里几个人组队参加着玩玩的(
谢谢。NOIP是初高中生的比赛是吧、
对(现在说是面向高中生……)
图呢?
???不是在吗(
orz主席树
庆历四年春,滕……【嘭!sxl打了wisher一巴掌】