标题:深入探索排序算法的性能比较
在这篇博文中,我们将探讨多种经典排序算法的性能表现。使用 C语言实现这些算法,并对其在相同随机数据集上的执行时间进行测试与分析。
代码概述
我们的代码实现了以下排序算法:
- 直接插入排序 (
Insertion Sort) - 折半插入排序 (
Binary Insertion Sort) - 希尔排序 (
Shell Sort) - 冒泡排序 (
Bubble Sort) - 快速排序 (
Quick Sort) - 简单选择排序 (
Selection Sort) - 堆排序 (
Heap Sort) - 归并排序 (
Merge Sort) - 基数排序 (
Radix Sort) - 计数排序 (
Counting Sort) - 每种算法都被封装在一个函数中,并通过函数指针来调用。为了公平比较,我们在相同大小的随机数组上多次测试每个算法,并记录其执行时间。
实验设置
数组大小:100,000
测试次数:10次
随机数生成:使用当前时间作为种子生成不同的随机数组
在测试过程中,我们将执行以下步骤:
生成随机数据集。
对每种排序算法进行排序,并记录用时。
将结果输出到 CSV 文件,便于后续分析和可视化。
源代码
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define NUM_ALGORITHMS 10 // 排序算法数量
#define ARRAY_SIZE 1000 // 测试数组大小
#define NUM_TESTS 1 // 测试次数
// 排序算法函数声明
void insertion_sort(int arr[], int n);
void binary_insertion_sort(int arr[], int n);
void shell_sort(int arr[], int n);
void bubble_sort(int arr[], int n);
void quick_sort_adapter(int arr[], int n);
void quick_sort(int arr[], int left, int right);
void selection_sort(int arr[], int n);
void heap_sort(int arr[], int n);
void merge_sort_adapter(int arr[], int n);
void merge_sort(int arr[], int temp[], int left, int right);
void radix_sort(int arr[], int n);
void counting_sort(int arr[], int n);
// 定义排序函数指针类型
typedef void (*SortFunction)(int arr[], int n);
void test_sort(const char *name, SortFunction sort_func, const int arr[], int n, FILE *file) {
int *copy = malloc(n * sizeof(int));
if (!copy) {
fprintf(stderr, "内存分配失败\n");
exit(1);
}
for (int i = 0; i < n; i++) copy[i] = arr[i];
clock_t start = clock();
sort_func(copy, n); // 执行排序
clock_t end = clock();
// 打印排序结果(仅显示部分元素)
printf("%s 排序后部分数据: ", name);
for (int i = 0; i < (n < 10 ? n : 10); i++) printf("%d ", copy[i]);
printf("\n... 用时: %.3f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
// 将结果写入文件
fprintf(file, "%s,%.3f\n", name, (double)(end - start) / CLOCKS_PER_SEC);
free(copy);
}
int main() {
FILE *file = fopen("sort_results.csv", "w");
if (!file) {
fprintf(stderr, "无法打开文件\n");
return 1;
}
fprintf(file, "Algorithm,Time\n"); // 写入CSV标题
// 定义排序算法的名称和对应的函数
const char *algorithm_names[] = {
"Insertion Sort", "Binary Insertion Sort", "Shell Sort",
"Bubble Sort", "Quick Sort", "Selection Sort",
"Heap Sort", "Merge Sort", "Radix Sort", "Counting Sort"
};
SortFunction algorithms[] = {
insertion_sort, binary_insertion_sort, shell_sort,
bubble_sort, quick_sort_adapter, selection_sort,
heap_sort, merge_sort_adapter, radix_sort, counting_sort
};
// 测试每种排序算法
for (int test = 0; test < NUM_TESTS; test++) {
int arr[ARRAY_SIZE];
srand(time(NULL) + test); // 使用不同的种子生成随机数组// NOLINT
// 生成随机测试数据
for (int i = 0; i < ARRAY_SIZE; i++) arr[i] = rand() % 10000;// NOLINT
for (int i = 0; i < NUM_ALGORITHMS; i++) {
printf("测试算法: %s\n", algorithm_names[i]);
test_sort(algorithm_names[i], algorithms[i], arr, ARRAY_SIZE, file);
printf("\n");
}
}
fclose(file);
return 0;
}
/*
// 测试每种排序算法
void test_sort(const char *name, SortFunction sort_func, int arr[], int n) {
int *copy = malloc(n * sizeof(int));
if (!copy) {
fprintf(stderr, "内存分配失败\n");
exit(1);
}
for (int i = 0; i < n; i++) copy[i] = arr[i];
clock_t start = clock();
sort_func(copy, n); // 执行排序
clock_t end = clock();
// 打印排序结果(仅显示部分元素)
printf("%s 排序后部分数据: ", name);
for (int i = 0; i < (n < 10 ? n : 10); i++) printf("%d ", copy[i]);
for (int i = 0; i < n - 1; i++) {//检查是否满足排序
if (copy[i] <= copy[i + 1])
{
if(i == n - 2)
printf("\n排序成功\n");
continue;
}
else {
// printf("\n排序失败%d\t%d\n", i, copy[i]);
}
}
// for (int i = 0; i < n; i++) printf("%d ", copy[i]);
printf("\n... 用时: %.3f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
free(copy);
}
int main() {
int arr[ARRAY_SIZE];
srand(time(NULL));
// 生成随机测试数据
for (int i = 0; i < ARRAY_SIZE; i++) arr[i] = rand() % 10000;
// 定义排序算法的名称和对应的函数
const char *algorithm_names[] = {
"Insertion Sort", "Binary Insertion Sort", "Shell Sort",
"Bubble Sort", "Quick Sort", "Selection Sort",
"Heap Sort", "Merge Sort", "Radix Sort", "Counting Sort"
};
SortFunction algorithms[] = {
insertion_sort, binary_insertion_sort, shell_sort,
bubble_sort, quick_sort_adapter, selection_sort,
heap_sort, merge_sort_adapter, radix_sort, counting_sort
};
// 测试每种排序算法
for (int i = 0; i < NUM_ALGORITHMS; i++) {
// for (int i = 0; i < 10; i++) {
printf("测试算法: %s\n", algorithm_names[i]);
test_sort(algorithm_names[i], algorithms[i], arr, ARRAY_SIZE);
printf("\n");
}
return 0;
}
*/
// 各种排序算法的实现(待填充)
/*
void insertion_sort(int arr[], int n) {
int temp;
for(int i = 1; i < n; i ++ )
{
if(arr[i] < arr[i - 1])
{
temp = arr[i];
int j;
for (j = i - 1; j >= 0 && arr[j] > temp; j -- )
{
arr[j + 1] = arr[j];
}
arr[j + 1] = temp;
}
}
}
*/
void insertion_sort(int arr[], int n) {
// 从数组的第二个元素开始,逐个向前插入到已排序的部分
for (int i = 1; i < n; i++) {
int temp = arr[i]; // 将当前元素存储在 temp 中
int j = i - 1; // j 指向当前元素前一个位置
// 内循环:将比 temp 大的元素向右移动
while (j >= 0 && arr[j] > temp) {
arr[j + 1] = arr[j]; // 把比 temp 大的元素向右移动一位
j--; // j 向前移动一位,继续比较前一个元素
}
// 找到 temp 的正确位置,将其放入
arr[j + 1] = temp;
// 当内循环结束时,j+1 正是 temp 应该插入的位置
}
}
void binary_insertion_sort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int temp = arr[i]; // 暂存待插入的元素
int l = 0, r = i - 1; // 二分查找的左右边界
// 使用二分查找确定插入位置
while (l <= r) {
int mid = (l + r) / 2; // 计算中点
if (arr[mid] > temp) {
r = mid - 1; // 搜索左半部分
} else {
l = mid + 1; // 搜索右半部分
}
}
// 将大于 temp 的元素向右移动一位
for (int j = i - 1; j >= l; j--) {
arr[j + 1] = arr[j];
}
arr[l] = temp; // 将 temp 插入到正确位置
}
}
void shell_sort(int arr[], int n) {
// 初始增量设置为数组长度的一半
for (int gap = n / 2; gap > 0; gap /= 2) {
// 对于当前增量,进行插入排序
for (int i = gap; i < n; i++) {
int temp = arr[i]; // 暂存当前元素
int j; // j 用于遍历间隔内的已排序部分
// 内循环:在当前增量下,将 arr[i] 插入到合适的位置
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
arr[j] = arr[j - gap]; // 将大于 temp 的元素向后移动
}
// 将 temp 插入到找到的位置
arr[j] = temp; // j 指向 temp 应插入的位置
}
}
}
// void shell_sort(int arr[], int n) {
// int temp;
// for(int dk = n / 2; dk > 0; dk = dk / 2) {
// for(int i = dk; i < n; i++) {
// if(arr[i] < arr[i - dk]) {
// temp = arr[i];
// int j = i - dk;
// for(j = i - dk; j >= 0&&arr[j] < temp; j = j - dk) {
// arr[j + dk] = arr[j];
// }
// arr[j + dk] = temp;
// }
//
// }
// }
// }
void bubble_sort(int arr[], int n) {
// 外层循环控制排序的轮数
for (int i = 0; i < n - 1; i++) {
// 内层循环进行相邻元素的比较和交换
for (int j = 0; j < n - 1 - i; j++) {
// 如果前一个元素大于后一个元素,则交换它们
if (arr[j] > arr[j + 1]) {
// 交换元素
int temp = arr[j]; // 暂存当前元素
arr[j] = arr[j + 1]; // 将后一个元素放到前面
arr[j + 1] = temp; // 将暂存的元素放到后面
}
}
}
}
void quick_sort_adapter(int arr[], int n) {
quick_sort(arr, 0, n - 1);
}
void quick_sort(int arr[], int l, int r) { // NOLINT
// 如果左指针大于或等于右指针,说明数组已排序,直接返回
if(l >= r) return;
// 初始化指针和基准值
int i = l - 1, j = r + 1, x = arr[(l + r) / 2];
// 当 i 小于 j 时继续执行
while(i < j) {
// 从左侧找到第一个大于等于基准值的元素
do i++; while(arr[i] < x);
// 从右侧找到第一个小于等于基准值的元素
do j--; while(arr[j] > x);
// 如果 i 小于 j,交换 arr[i] 和 arr[j]
if(i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// 递归调用,对左侧和右侧的子数组进行排序
quick_sort(arr, l, j);
quick_sort(arr, j + 1, r);
}
void selection_sort(int arr[], int n) {
// 外层循环控制已排序部分的边界
for(int i = 0; i < n - 1; i++) {
// 假设当前索引 i 是最小值的索引
int min = i;
// 内层循环寻找未排序部分的最小值
for(int j = i + 1; j < n; j++) {
// 如果找到更小的元素,更新最小值的索引
if(arr[j] < arr[min]) {
min = j;
}
}
// 如果最小值的索引不等于当前索引 i,进行交换
if(min != i) {
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
}
// h[N] 存储堆中的值,h[1] 是堆顶
// ph[k] 存储第 k 个插入的点在堆中的位置
// hp[k] 存储堆中下标是 k 的点是第几个插入的
int h[ARRAY_SIZE + 10], ph[ARRAY_SIZE + 10], hp[ARRAY_SIZE + 10], size;
// 交换两个点及其映射关系
void heap_swap(int a, int b) {
// 交换映射
int temp = ph[hp[a]];
ph[hp[a]] = ph[hp[b]];
ph[hp[b]] = temp;
// 交换索引映射
temp = hp[a];
hp[a] = hp[b];
hp[b] = temp;
// 交换堆中的值
int value = h[a];
h[a] = h[b];
h[b] = value;
}
// 向下调整堆,使堆满足性质
void down(int u) { // NOLINT
int t = u; // 初始化当前节点为最小值
if (u * 2 <= size && h[u * 2] > h[t]) t = u * 2; // 左子节点
if (u * 2 + 1 <= size && h[u * 2 + 1] > h[t]) t = u * 2 + 1; // 右子节点
//小根堆写法
// if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2; // 左子节点
// if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1; // 右子节点
if (u != t) { // 如果 t 发生变化,进行交换并继续向下调整
heap_swap(u, t);
down(t);
}
}
// 向上调整堆,使堆满足性质
void up(int u) {
while (u / 2 && h[u] < h[u / 2]) {
heap_swap(u, u / 2);
u >>= 1; // 移动到父节点
}
}
// 建堆:O(n) 的时间复杂度
void build_heap(const int arr[], int n) {
size = n; // 设置堆的大小
// 将数组的值复制到堆中
for (int i = 1; i <= n; i++) {
h[i] = arr[i - 1];
}
// 从最后一个非叶子节点开始,向下调整
for (int i = n / 2; i > 0; i--) {
down(i);
}
}
// 堆排序
void heap_sort(int arr[], int n) {
// 建立最小堆
build_heap(arr, n);
// 逐步提取元素,构建排序
for (int i = n; i > 1; i--) {
// 将堆顶元素(最小值)与当前最后一个元素交换
heap_swap(1, i);
size--; // 减少堆的大小
down(1); // 重新调整堆
}
// 将排序结果存回原数组
for (int i = 1; i <= n; i++) {
arr[i - 1] = h[i]; // 从堆中提取元素并存入原数组
}
}
void merge_sort(int arr[], int temp[], int left, int right) { // NOLINT
// 如果左边界大于或等于右边界,说明该部分已排序或没有元素,直接返回
if (left >= right) return;
// 计算中间位置
int mid = left + (right - left) / 2;
// 递归地对左半部分进行归并排序
merge_sort(arr, temp, left, mid);
// 递归地对右半部分进行归并排序
merge_sort(arr, temp, mid + 1, right);
// 初始化临时数组的索引 k 和左右子数组的起始索引 i 和 j
int k = left; // 临时数组的起始索引
int i = left; // 左子数组的起始索引
int j = mid + 1; // 右子数组的起始索引
// 合并两个已排序的子数组
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++]; // 将左边的元素放入临时数组
} else {
temp[k++] = arr[j++]; // 将右边的元素放入临时数组
}
}
// 将左子数组中剩余的元素放入临时数组
while (i <= mid) {
temp[k++] = arr[i++];
}
// 将右子数组中剩余的元素放入临时数组
while (j <= right) {
temp[k++] = arr[j++];
}
// 将临时数组中的元素复制回原数组
for (i = left; i <= right; i++) {
arr[i] = temp[i]; // 将排序后的元素放回原数组
}
}
// 适配器函数,负责初始化临时数组并调用归并排序
void merge_sort_adapter(int arr[], int n) {
int temp[n]; // 创建临时数组
merge_sort(arr, temp, 0, n - 1); // 调用归并排序
}
void counting_sort(int arr[], int n) {
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
int count[max + 1]; // 计数数组,大小为最大值+1
int output[n]; // 输出数组
// 初始化计数数组
for (int i = 0; i <= max; i++) {
count[i] = 0;
}
// 统计每个元素的出现次数
for (int i = 0; i < n; i++) {
count[arr[i]]++;
}
// 更新计数数组,使其包含元素的实际位置
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// 构建输出数组
for (int i = n - 1; i >= 0; i--) {
output[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}
// 将排序后的元素复制回原数组
for (int i = 0; i < n; i++) {
arr[i] = output[i];
}
}
// 链表节点表示队列
typedef struct Node {
int data;
struct Node* next;
} Node;
// 创建新节点
Node* create_node(int data) {
Node* new_node = (Node*)malloc(sizeof(Node));
new_node->data = data;
new_node->next = NULL;
return new_node;
}
// 队列操作
typedef struct Queue {
Node* front;
Node* rear;
} Queue;
// 初始化队列
void init_queue(Queue* q) {
q->front = NULL;
q->rear = NULL;
}
// 入队
void enqueue(Queue* q, int data) {
Node* new_node = create_node(data);
if (q->rear) {
q->rear->next = new_node;
} else {
q->front = new_node;
}
q->rear = new_node;
}
// 出队
int dequeue(Queue* q) {
if (!q->front) return -1; // 队列为空
Node* temp = q->front;
int data = temp->data;
q->front = q->front->next;
if (!q->front) {
q->rear = NULL; // 队列空时重置
}
free(temp);
return data;
}
// 检查队列是否为空
int is_empty(const Queue* q) {
return q->front == NULL;
}
// 获取某一位的数字
int get_digit(int number, int digit) {
return (number / (int)pow(10, digit)) % 10;
}
// 基数排序
void radix_sort(int arr[], int n) {
Queue queues[10]; // 10个队列
for (int i = 0; i < 10; i++) {
init_queue(&queues[i]);
}
// 找到最大值
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// 对每一位进行排序
for (int digit = 0; digit < (int)log10(max) + 1; digit++) {
// 入队
for (int i = 0; i < n; i++) {
int d = get_digit(arr[i], digit);
enqueue(&queues[d], arr[i]);
}
// 出队
int index = 0;
for (int i = 0; i < 10; i++) {
while (!is_empty(&queues[i])) {
arr[index++] = dequeue(&queues[i]);
}
}
}
}
画图py代码
import pandas as pd
import matplotlib.pyplot as plt
# 读取 CSV 文件
data = pd.read_csv('sort_results.csv')
# 计算每个算法的平均时间
average_times = data.groupby('Algorithm').mean()
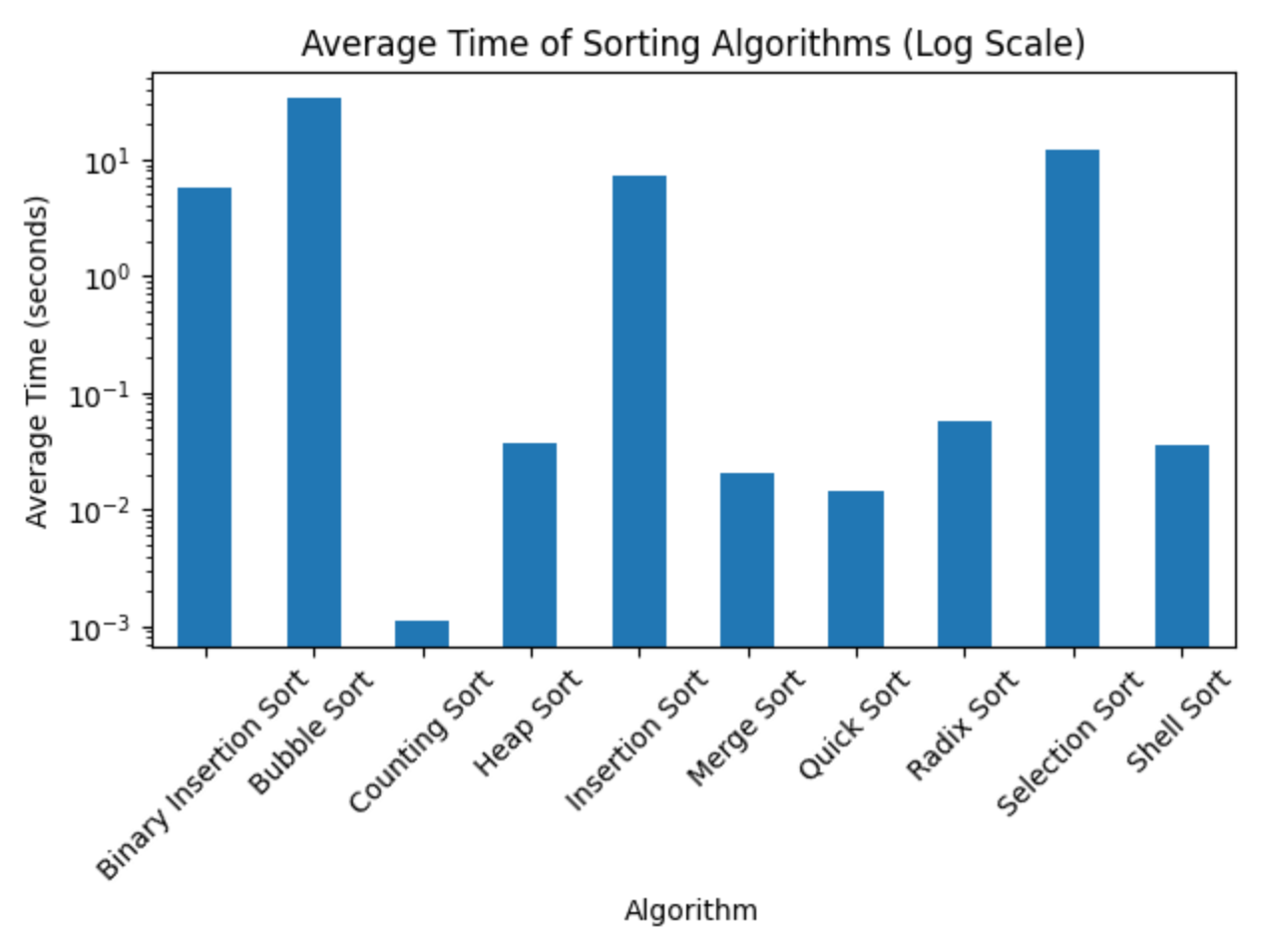
# 绘制柱状图,使用对数刻度
plt.figure(figsize=(10, 6))
average_times.plot(kind='bar', legend=False)
plt.title('Average Time of Sorting Algorithms (Log Scale)')
plt.ylabel('Average Time (seconds)')
plt.xlabel('Algorithm')
plt.yscale('log') # 使用对数刻度
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
import pandas as pd
import matplotlib.pyplot as plt
# 读取 CSV 文件
data = pd.read_csv('sort_results.csv')
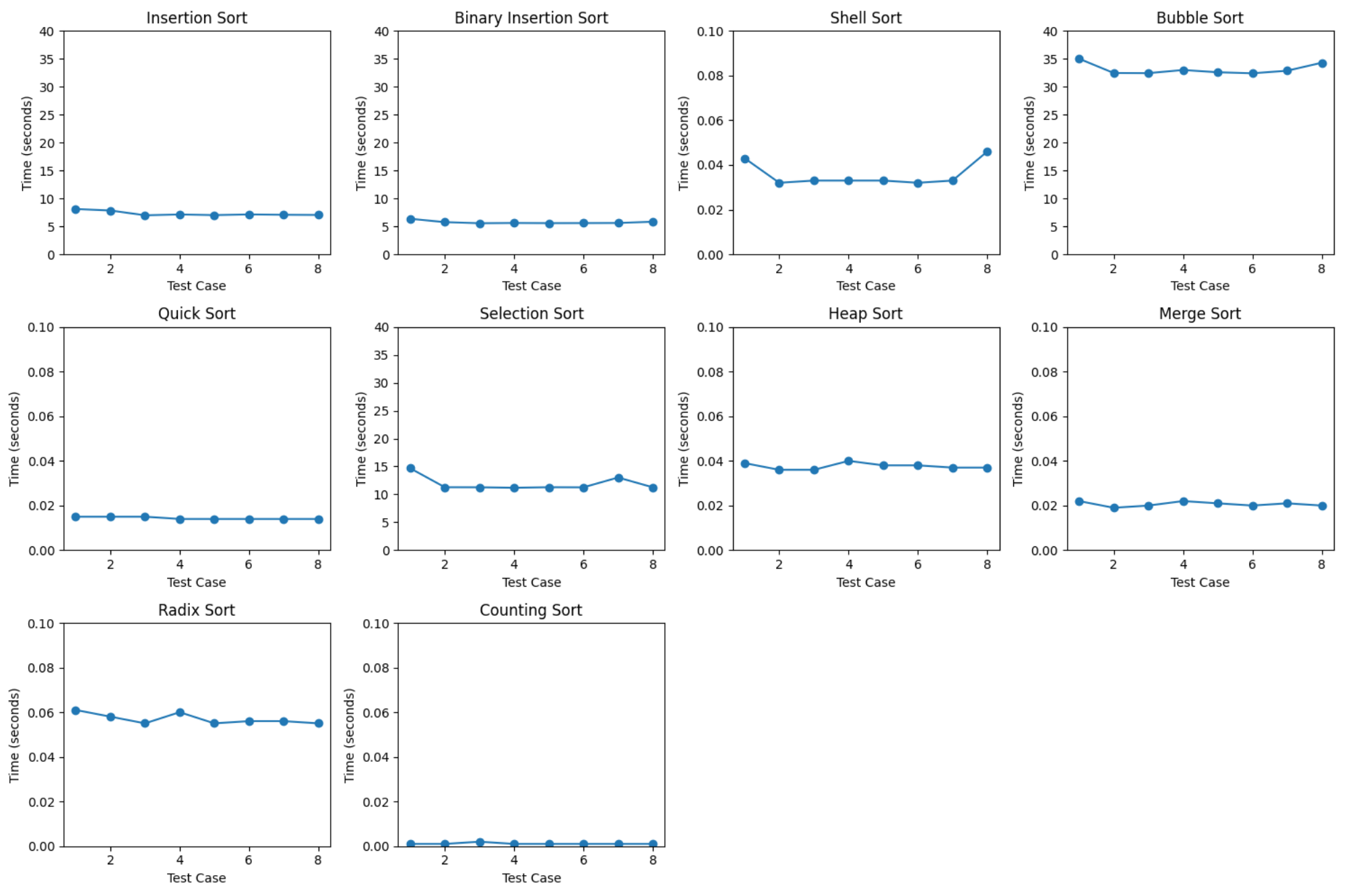
# 创建一个大图
fig, axs = plt.subplots(nrows=3, ncols=4, figsize=(15, 10))
axs = axs.flatten() # 将多维数组展平为一维数组
# 对每个算法进行绘图
for i, algorithm in enumerate(data['Algorithm'].unique()):
# 提取该算法的时间数据
times = data[data['Algorithm'] == algorithm]['Time']
# 绘制折线图
axs[i].plot(range(1, len(times) + 1), times, marker='o')
axs[i].set_title(algorithm)
axs[i].set_xlabel('Test Case')
axs[i].set_ylabel('Time (seconds)')
# 根据算法的特性调整 Y 轴范围
if algorithm in ['Insertion Sort', 'Binary Insertion Sort', 'Selection Sort', 'Bubble Sort']:
axs[i].set_ylim(0, 40) # 适合较慢的算法
elif algorithm in ['Shell Sort', 'Heap Sort', 'Merge Sort', 'Quick Sort']:
axs[i].set_ylim(0, 0.1) # 适合快速的算法
elif algorithm in ['Radix Sort', 'Counting Sort']:
axs[i].set_ylim(0, 0.1) # 适合最优化的算法
else:
axs[i].set_ylim(0, max(data['Time']) + 5) # 默认范围
# 隐藏多余的子图
for j in range(i + 1, len(axs)):
axs[j].axis('off')
# 调整布局
plt.tight_layout()
plt.show()

大佬!
做的比我好多了qwq