[TOC]

二叉树前序遍历

非递归遍历

使用栈来模拟递归的操作：循环条件：节点不为NULL，且栈不为空。

• 如果当前节点不为空，访问节点，并且把节点进栈，节点指向其左孩子，直至左孩子为空
• 这时相当于左子树已经遍历完了，我们需要访问右节点，将当前元素指向栈顶元素右孩子，弹出栈顶元素，

vector<int> preTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> st;
    TreeNode* cur = root;
    while(cur != NULL || !st.empty())
    {
        while(cur != NULL)
        {
                res.push_back(cur->val);
            st.push(cur);
            cur = cur->left;
        }
        TreeNode* p = st.top();
        st.pop();
        cur = p->right;
    }
    return res;
}

Morris前序遍历

Morris遍历可以使用$O(1)$的空间，但是时间会稍微慢一点。我们在遍历时使用栈的重要原因就是为了保存当前节点的右子树信息，以便我们在回溯的时候能够找到其右子树。Morris遍历则是使用另外一种方式达到同样的目的。我们首先定义一个节点的前继，以及搭桥和拆桥过程。

前继：该节点的左子树的最右孩子节点，这也是左子树中最后一个被遍历的元素，如果我们能从这个元素索引到根节点，那么我们就可以索引到根节点的右子树。

搭桥：将一个节点的前继的右子树指向该节点。

拆桥：将一个节点的前继的右子树恢复成NULL。

Morris前序遍历的流程如下：

• 如果当前节点的左孩子为空，访问该节点，并将当前节点的右孩子节点置为新节点。
• 如果当前节点的左孩子不为空，那么我们找到当前节点在左子树中的前继。
• 如果当前前继节点的右孩子为空，那么进行搭桥，并访问该节点，将当前节点左孩子置为新节点

• 否则，拆桥，当前节点更新为当前节点的右孩子。

• 重复上述过程直至节点为空。

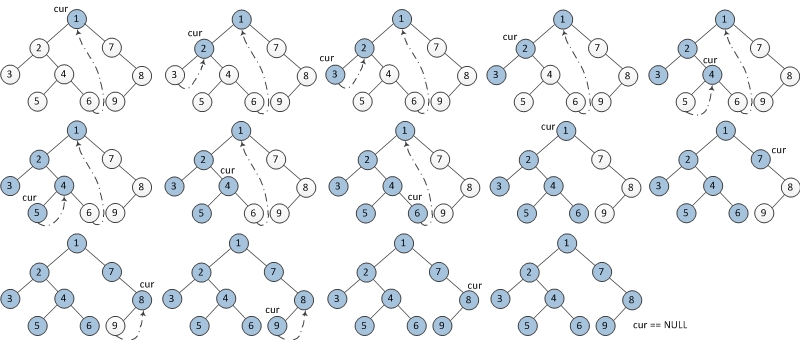
vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;

    while (root != NULL)
    {
        if(root->left == NULL)
        {
            res.push_back(root->val);
            root = root->right;
        }
        else
        {
            //  找到前继
            TreeNode* temp = root->left;
            while(temp->right != NULL && temp->right != root)
                temp = temp->right;
            //  搭桥
            if(temp->right == NULL)
            {
                temp->right = root;
                res.push_back(root->val);
                root = root->left;
            }
            //  拆桥
            else
            {
                temp->right = NULL;
                root = root->right;
            }
        }
    }
    return res;
}

二叉树中序遍历

非递归遍历

和前序遍历类似，只不过访问节点从第一次进栈时变成出栈时访问节点。

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> st;
    TreeNode* cur = root;
    while(cur != NULL || !st.empty())
    {
        while(cur != NULL)
        {
            st.push(cur);
            cur = cur->left;
        }
        TreeNode* p = st.top();
        st.pop();
        res.push_back(p->val);
        cur = p->right;
    }
    return res;
}

Morris中序遍历

和Morris前序遍历类似，只不过访问节点的时候从搭桥的时刻变成拆桥的时刻。

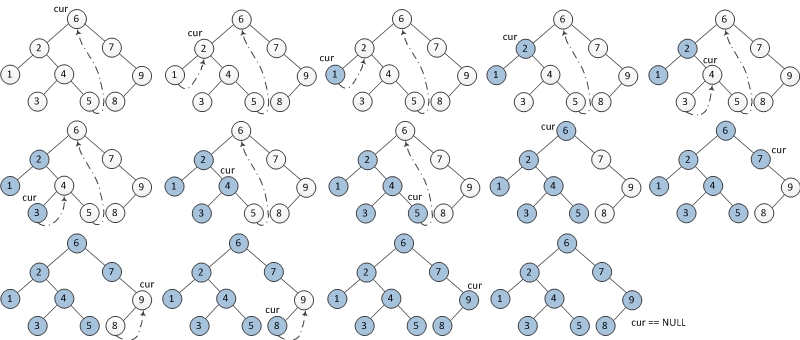
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;    
    while (root != NULL)
    {
        if(root->left == NULL)
        {
            res.push_back(root->val);
            root = root->right;
        }
        else
        {
            TreeNode* temp = root->left;
            while(temp->right != NULL && temp->right != root)
                temp = temp->right;
            if(temp->right == NULL)
            {
                temp->right = root;
                root = root->left;
            }
            else
            {
                temp->right = NULL;
                res.push_back(root->val);
                root = root->right;
            }
        }
    }
    return res;
}

二叉树后序遍历

非递归后序遍历

后序遍历的难点在于第一次将根节点出栈后，并不能直接访问，必须访问其右子树后才可以。非递归后序遍历有很多种实现方式，我个人比较喜欢，使用一个状态栈来存储栈中元素的状态，状态为0暂时不可访问，状态为1可以访问。

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> st1;
    stack<int> st2;
    TreeNode* cur = root;
    while(cur != NULL || !st1.empty())
    {
        while(cur != NULL)
        {
            st1.push(cur);
            st2.push(0);
            cur = cur->left;
        }
        TreeNode* p = st1.top();
        if(st2.top() == 0)
        {
            st2.top() = 1;
            cur = p->right;
        }else
        {
            st1.pop();
            st2.pop();
            res.push_back(p->val);
        }
    }
    return res;
}

Morris后序遍历

Morris后序遍历就比较麻烦了，步骤如下：

• 设置一个虚拟头节点，虚拟头节点的左孩子指向根节点。当前节点从虚拟头节点开始
• 如果当前节点的左孩子为空，则将其右孩子作为当前节点。
• 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点的前继
• 如果前继的右孩子为空，搭桥，当前节点的左孩子成为新节点
• 如果前继的右孩子为当前节点，逆序输出从当前节点的左孩子到前继节点路径上的节点。拆桥。当前节点的右孩子成为新节点。
  

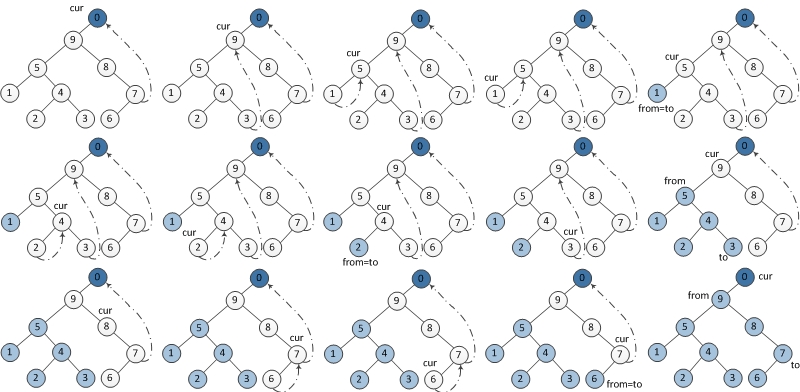
//  反转这条路径
void reverse(TreeNode *source, TreeNode *target)
{
    if (source == target)
        return;
    TreeNode *pre = source, *cur = source->right, *temp;
    while (pre != target)
    {
        temp = cur->right;
        cur->right = pre;
        pre = cur;
        cur = temp;
    }
}

void saveNode(TreeNode* source, TreeNode *target)
{
    reverse(source, target);

    TreeNode *p = target;
    while (true)
    {
        res.push_back(p->val);
        if (p == source)
            break;
        p = p->right;
    }
    reverse(target, source);
}

vector<int> postorderTraversal(TreeNode* root)
{
    TreeNode* dummy = new TreeNode(0);
    dummy->left = root;
    TreeNode* cur = dummy;
    while(cur != NULL)
    {
        if(cur->left == NULL)
            cur = cur->right;
        else
        {
            TreeNode* temp = cur->left;
            while(temp->right != NULL && temp->right != cur)
                temp = temp->right;
            if(temp->right == NULL)
            {
                temp->right = cur;
                cur = cur->left;
            }
            else
            {
                saveNode(cur->left,temp);
                temp->right = NULL;
                cur = cur->right;
            }
        }
    }
    return res;
}

二叉树层次遍历

二叉树的层次遍历通常情况下借助于队列实现。当根节点不为空时，将根节点加入队列。当队列不为空的时候，访问队列头元素，同时将队头元素的非空子节点进队列，将队头元素出栈。

vector<int> levelTraversal(TreeNode* root)
{
    vector<int> res;
    queue<TreeNode*> q;
    if(root == NULL) return res;
    q.push(root);
    while(!q.empty())
    {
        TreeNode* cur = q.front();
        q.pop();
        res.push_back(cur->val);
        if(cur.left != NULL) q.push(cur->left);
        if(cur.right != NULL) q.push(cur->right);
    }
    return res;
}

有时候，题目会要求我们把每一层的节点分别保存，所以我们还需要保存其层次信息，我通常使用两种做法：

• 将节点和层次信息打包成pair[HTML_REMOVED]存到队列中。

    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if(root == NULL) return res;
        queue<pair<TreeNode*,int>> q;
        q.push({root,0});
        while(!q.empty())
        {
            auto t = q.front();
            q.pop();
            if(t.second == res.size())
                res.push_back({});
            res[t.second].push_back(t.first->val);
            if(t.first->left != NULL) q.push({t.first->left,t.second + 1});
            if(t.first->right != NULL) q.push({t.first->right,t.second + 1});
        }
        return res;
    }

• 保存当前层节点有多少个节点，以及当前层已经访问了多少个节点。

vector<vector<int>> levelOrder(TreeNode* root)
{
    vector<vector<int>> res;
    queue<TreeNode*> q;
    if(root == NULL) return res;
    q.push(root);
    //  当前层总共节点数，当前层已经访问节点树，当前第几层
    int size = 1,cur_size = 0,level = 0;
    while(!q.empty())
    {
      TreeNode* cur = q.front();
      q.pop();
      if(res.size() == level)
        res.push_back({cur->val});
      else
        res[level].push_back(cur->val);
      if(cur->left != NULL) q.push(cur->left);
      if(cur->right != NULL) q.push(cur->right);
        if(++ cur_size == size)
      {

        cur_size = 0;
        size = q.size();
              level ++;
      }
    }
    return res;
}

DFS遍历

也有的时候，题目只需要得到某一层的最大值，最小值，第一个节点，最后一个节点之类的，我们就没有必要严格按照层次遍历的顺序了。可以使用dfs来遍历每一层的节点。注意：这不是真正的层次遍历。

vector<vector<int>> res;
void dfs(TreeNode* root,int level)
{
    if(root == NULL) return;
    if(res.size() == level)
        res.push_back({});
    res[level].push_back(root->val);
    dfs(root->left,level + 1);
    dfs(root->right,level + 1);
}