$\Huge\color{orchid}{点击此处获取更多干货}$

序列式与关联式

序列式结构就是之前提到的线性表（顺序表和链表），其中的元素或者节点都有且仅有唯一的前驱和后继，而关联式结构中某元素或节点，可能存在多个前驱，多个后继，树和图就是关联式结构的两种典例

树结构

树结构分为定根树和不定根树，以及有向树与无向树，下面以定根的有向树为例，介绍几个基本定义和性质：
1. 树结构中每个节点最多只能有一个前驱，但可以有无数个后继（前驱和后继可以没有，但不能是自身）
2. 树中没有前驱节点的为根节点，没有后继节点的为叶子节点，如果树结构只含有根节点，可以叫做“平凡树”，一个节点都没有的树叫做“空树”
3. 每个节点含有自身的信息和后继节点的地址（可以是指针也可以是索引），节点的后继又可以叫做“孩子”，节点的前驱可以叫“双亲”（考研408数据结构定义），也可以叫“父亲”（联想到类间继承关系“父类”和“子类”，而且前驱保证唯一，“父亲”更合适）
4. 树节点的度为该节点的孩子数量，节点的最大度$M$为整个树结构的度，该树可以称作“$M$叉树”
5. 树节点的数量一定比边的数量多1，如果用$c_i$表示度为$i$的节点数量，$M$表示树的度，那么下面的等式一定成立：$ {\textstyle \sum_{i=0}^{M}} c_i = {\textstyle \sum_{i=0}^{M}} (i*c_i) + 1$（对于考研党来说这个很有用）
6. 树中节点有“深度”的概念，根节点深度为1，从根节点沿着孩子节点的指针一路往下走，每走一步，对应节点的深度+1，到达叶子节点为止。叶子节点中的最大深度为树的深度（或高度）
7. $M$叉树深度为$d$的层级能够容纳的最大节点数量为$M^{d-1}$，截至$d$的深度，最多能含有的节点数量为$N=\sum_{i=1}^{d}(M^{i-1}) = (1-M^d)/(1-M)$

下图是一个可能的例子：

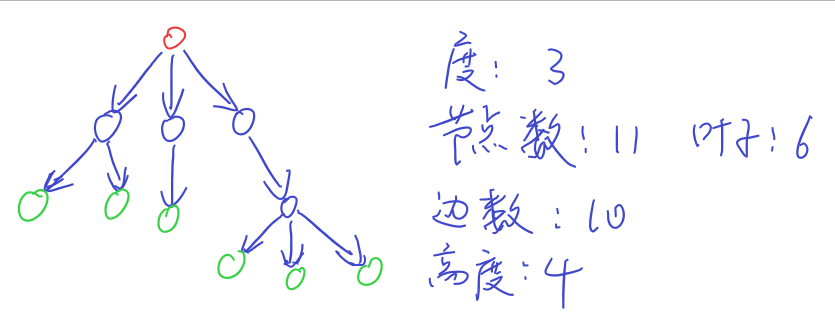
少数情况下，树结构用序列式存储更加方便，但大多数情况下，树结构用分叉链表存储更好，以这种方式存储时，树节点的结构体定义如下：（C++泛型版，借此回顾一下字典树）

template<class ElemType>
struct Node {
    ElemType val;//自身信息
    Node<ElemType>** child;//后继节点列表，长度为树的度数
};

遍历树的方式有先根序（先序），后根序（后序），层序等方式，对于比较特殊的二叉树，还有中根序（中序）遍历方式。下面给出四种遍历方式的C++版代码实现：

//先序（根左右）
void preorder(Node* root) {
    if (root == nullptr) {
        return;
    }
    visit(root);//抽象地代指访问节点操作
    preorder(root->lchild);
    preorder(root->rchild);
}

//中序（左根右）
void inorder(Node* root) {
    if (root == nullptr) {
        return;
    }
    inorder(root->lchild);
    visit(root);
    inorder(root->rchild);
}

//后序（左右根）
void postorder(Node* root) {
    if (root == nullptr) {
        return;
    }
    postorder(root->lchild);
    postorder(root->rchild);
    visit(root);
}

//层序
void levelorder(Node* root) {
    queue<Node*> q;//需要借助队列
    q.push(root);
    while (!q.empty()) {
        Node* cur = q.front();
        q.pop();
        visit(cur);
        if (cur->lchild != nullptr) {
            q.push(cur->lchild);
        }
        if (cur->rchild != nullptr) {
            q.push(cur->rchild);
        }
    }
}

对于度数为$M$，高度为$d$的二叉树，还有以下三个概念：
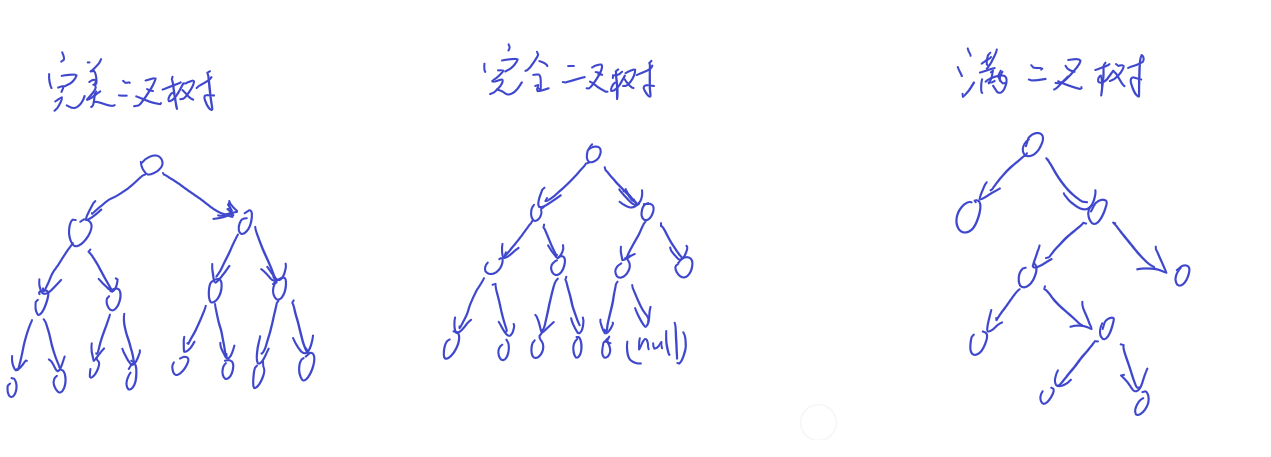
1. 完美二叉树：所有叶子节点都位于深度最大的层，且每一层节点都达到了该层能容纳的最大节点数量$M^{d-1}$（如左侧所示）
2. 完全二叉树：每个节点的位置都和相同层数的完美二叉树节点位置相同（如中间所示），优先级队列（堆）采用该数据结构，可以用序列存储
3. 满二叉树：非叶子节点的左右孩子都不是空指针（如右侧所示）

图结构

下面给出图结构的一些定义和性质：
1. 图中的节点，前驱和后继数量都可以有多个。直接连接两个节点的路径叫做边或者弧，它可以有自身的权值，指明了方向的叫有向边，未指明方向的叫无向边（相当于两条有向边），每条边都是无向边的叫做无向图，否则就是有向图。边上带权值的图叫带权图，不带权值的就是无权图
2. 两个节点之间可能存在不止一条边，一条边的起点和终点可能是同一个节点，以上现象分别为“重边”和“自环”现象，如果一个图结构中这两种现象都不包含，那么这个图为“简单图”（考研408数据结构定义），从第3条开始，全部默认简单图
3. 由图中某些节点和边组成的新图，叫做这个图的子图。无向图中若任意两个节点都相互可达，则称这个图为“连通图”，图的连通子图叫做“连通分量”；在有向图中，相同情况被成为“强连通图”“强连通分量”，如果一个有向图自身不是强连通图，但是去掉边的方向后构成的新无向图为连通图，则该有向图为“弱连通图”，该图的弱连通子图叫“弱连通分量”
4. 无向图中，如果节点数量为$N$，一个节点最多和$(N-1)$个节点相连，如果每一个节点都与图中其他所有节点相连，那么该图为“完全图”，记作$K_N$，其节点数量为$N*(N-1)/2$
5. $N$个节点的无向连通图中，最少含有$(N-1)$条边（即为树的情况）
6. 要保证$N$个节点的无向图一定连通，至少含有$(N-1)*(N-2)/2+1$条边
7. 有向图中对于4，5，6三条，边数对应翻倍

在不考虑图的稀疏度的情况下，图的存储结构一般有三种：邻接矩阵、邻接表、链式前向星。下面给出这三种的示意图和C++代码实现：
邻接矩阵：

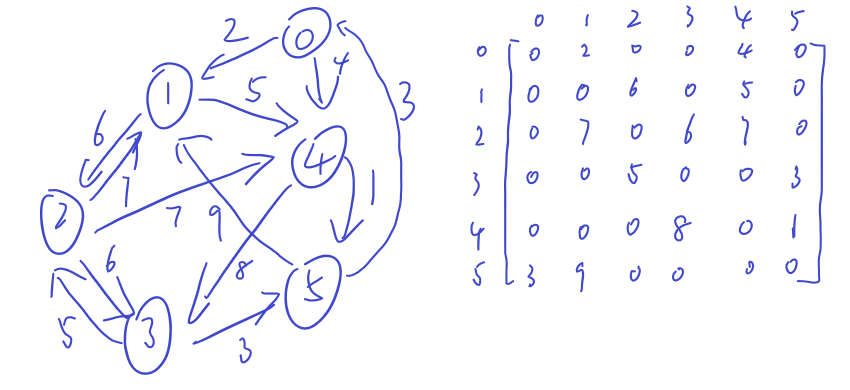
//邻接矩阵存储
class MGraph {
private:
    int** mat;
    //节点数，边数
    int numVex, numArc;
public:
    //n个节点，m条有向边
    MGraph(int n, int m) {
        numVex = n;
        numArc = m;
        mat = new int* [numVex];
        for (int i = 0; i < numVex; i++) {
            mat[i] = new int[numVex];
            fill(mat[i], mat[i] + numVex, 0);
        }
        //s,e,v分别代表起点，终点，权值
        size_t s, e;
        int v;
        while (m--) {
            cin >> s >> e >> v;
            //mat[s][e]=v表示从s到e的边权值为v
            mat[s][e] = v;
        }
    }

    ~MGraph() {
        for (int i = 0; i < numVex; i++) {
            delete[] mat[i];
        }
        delete[] mat;
    }
};

邻接表：

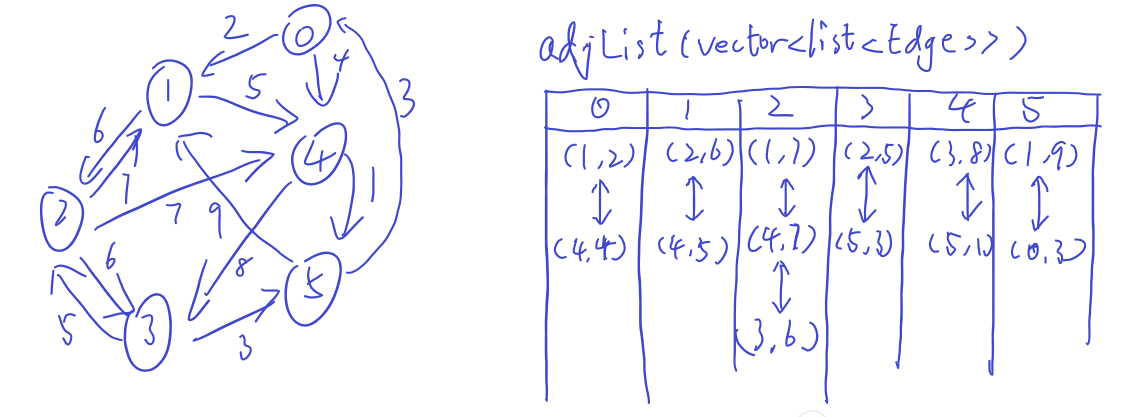
//邻接表存储
class ALGraph {
private:
    //结构体存储边信息（终点，权值）
    struct Edge {
        size_t nxt;
        int val;
        Edge() {}
        Edge(size_t nx, int v) : nxt(nx), val(v) {}
    };
    vector<list<Edge>> adjList;//邻接表，长度为节点数，每个位置存储对应节点的后继边
    int numVex, numArc;
public:
    ALGraph(int n, int m) {
        numVex = n;
        numArc = m;
        adjList.resize(numVex);
        size_t s, e;
        int v;
        while (m--) {
            cin >> s >> e >> v;
            adjList[s].push_back(Edge(e, v));
        }
    }
};

链式前向星：

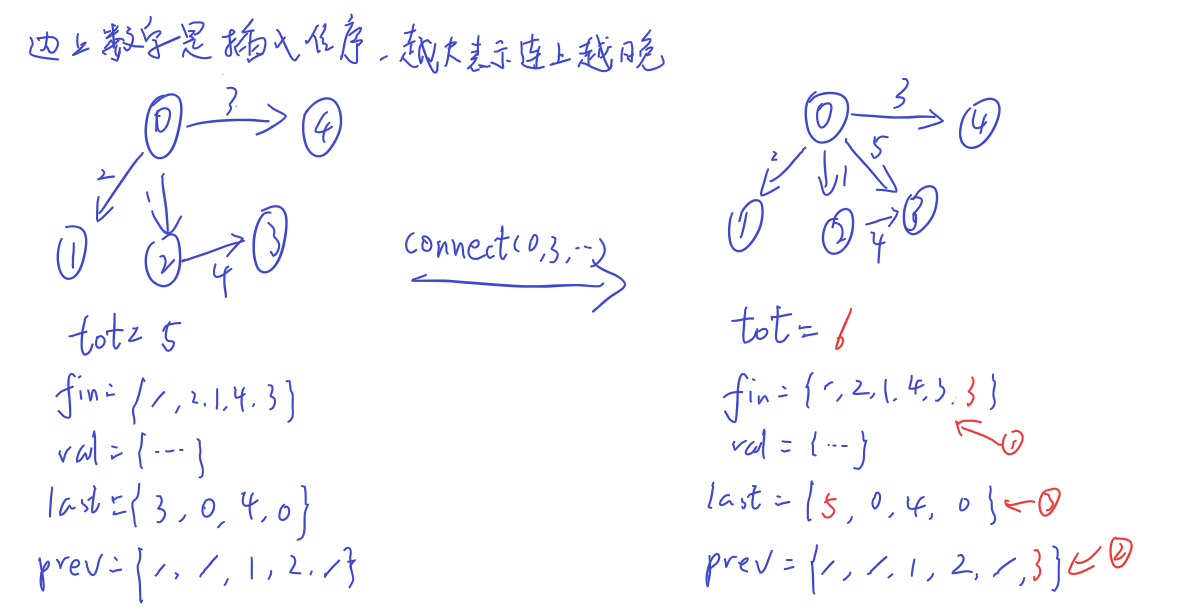
//链式前向星存储
class LinkGraph {
private:
    size_t* fin;            //边终点表
    int* val;               //边权值表
    size_t* last;           //节点末位边索引表，代表每个节点的后继边中，最后被连接上的边索引（0代表结束）
    size_t* prev;           //边的前向边索引表，代表每条边在其前驱节点上，在此前一位被连上的边索引
    int tot = 1;            //边的插入位序（如果后续要取反向边，初值建议改为2）
    int numVex, numArc;     //节点数和边数

    //单向连接
    void connect(int s, int e, int v) {
        //第一步，记录终点和权值
        fin[tot] = e;
        val[tot] = v;
        //第二步，将起点的last值赋给tot的prev值，表示位序tot的边的前向边为起点s原先的末位边last[s]
        prev[tot] = last[s];
        //第三步，此时起点s末位插入的边为tot，修改last[s]为tot，然后tot自增
        last[s] = tot++;
    }

public:
    LinkGraph(int n, int m) {
        numVex = n;
        numArc = m;
        fin = new size_t[numArc + 1];
        val = new int[numArc + 1];
        last = new size_t[numVex];
        prev = new size_t[numArc + 1];
        //全部初始化为0，此时每个节点都没有后继边
        fill(last, last + numVex, 0);
        size_t s, e;
        int v;
        while (m--) {
            cin >> s >> e >> v;
            connect(s, e, v);
        }
    }

    ~LinkGraph() {
        delete[] fin, val, last, prev;
    }
};

图有深度优先遍历和广度优先遍历两种方式，树的先根序遍历和层序遍历与之相互对应，具体实现代码，会在后面放出