背包问题概述

有N个物品和容积为V的背包，每个物品有体积vi和价值wi两个属性，目标是在限定容量内，选择一些物品放入背包，使得背包中物品的总价值最高。

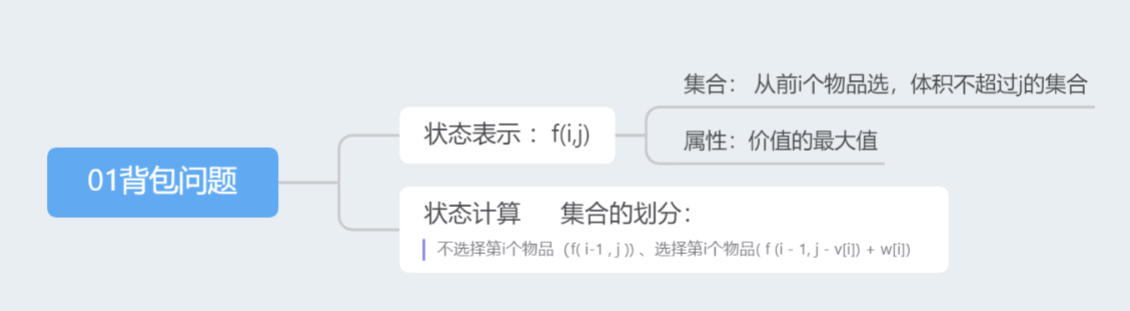
01背包问题

01背包问题
每件物品最多只能用一次或者不用；

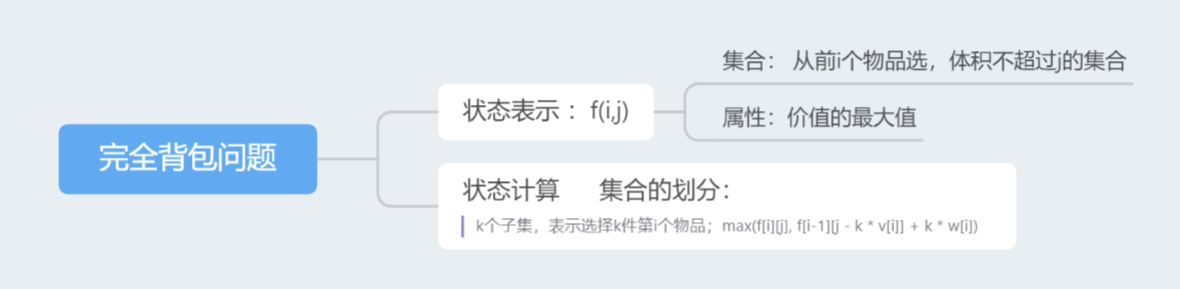
完全背包

完全背包问题
每件物品有无限个

优化：f[i][j] = max(f[i-1][j],f[i-1][j - 1 * v[i]] + w[i], f[i-1][j-2v[i]]+2w[i],.....)
f[i][j-v[i]] = max( f[i-1][j - 1 * v[i]], f[i - 1][j - 2 * v[i]] + w[i],..)
可得max(f[i-1][j - k * v[i]] + k * w[i]) = f[i][j - v[i]] + w[i]

多重背包问题

多重背包问题

每种物品只有si个，数量不一

朴素版本；类似完全背包问题,f[i][j] = max(f[i][j],f[i-1][j - k * v[i]] + k * w[i]) k = 1,2,3,…,s_i;

三重循环，时间复杂度(O(n^3);

优化

对第三层循环k进行优化，采用二进制的思想
若某物品有s_i个，则不需要枚举s_i次，而只需要logs_i次：
分成logs_i组：1，2，4，8，... , 2 ^ p, c;

其中c <= s_i

把原先的每组si件物品，拆分成1,2,4,8..等logsi组物品，每组有选和不选两种，则原问题转化为01背包问题

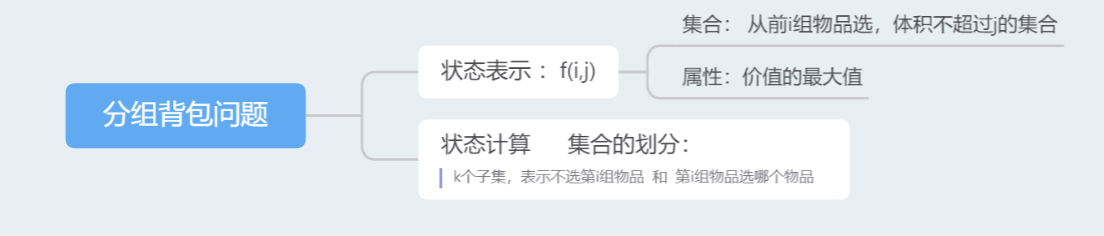
分组背包问题

物品有n组，每组里有若干个，只能从每个组中选一个（限定个）