《算法提高课》题解与笔记上线啦！(链接就是这个){: style=”color: #FF0000”}

创建时间2024-1-25

$$ #7 12.背包问题求具体方案 $$

背包求具体方案

原题Link

Code:

# include <bits/stdc++.h>
using namespace std;

const int N = 1e3 + 10;

int n, v, k;
int c[N], w[N], f[N][N];

int main(){
    scanf("%d %d", &n, &v);

    for(int i = 1; i <= n; i ++) scanf("%d %d", &c[i], &w[i]); // 输入的时候不能倒着输入 

    for(int i = n; i >= 1; i --){ // 倒着往前 ，求字典序 
        for(int j = 0; j <= v; j ++){
            f[i][j] = f[i + 1][j];
            if(j >= c[i]) f[i][j] = max(f[i][j], f[i + 1][j - c[i]] + w[i]); // 要有大于等于的条件 
        }
    }

    k = v;
    for(int i = 1; i <= n; i ++)
        if(k >= c[i] && f[i][k] == f[i + 1][k - c[i]] + w[i]) // 一定要大于等于c[i], 否则会错，要注意细节 ，优先选择选的方案（因为字典序） 
            printf("%d ", i), k -= c[i]; // 更新，下一次的物品容量不是这么大了 

    return 0;
}

思路

题目要求输出字典序最小的解，假设存在一个包含第1个物品的最优解，为了确保字典序最小那么我们必然
要选第一个。那么问题就转化成从 2~N 这些物品中找到最优解。之前的$ f(i,j) $记录的都是前$i$个物品总容量
为$ j $的最优解，那么我们现在将$ f(i,j) $定义为从第个元素到最后一个元素总容量为的最优解。接下来考虑
状态转移：
$ f(i,j)=\max(f(i+1,j),f(i+1,j-v[i])+w[i])$
两种情况，第一种是不选第$ i $个物品，那么最优解等同于从第$ i十1 $个物品到最后一个元素总容量为$ j $的最优
解：第二种是选了第$ i $个物品，那么最优解等于当前物品的价值$ w[i] $加上从第$ i十1 $个物品到最后一个元素总
容量为$ j一v[i] $的最优解。
计算完状态表示后，考虑如何的到最小字典序的解。首先$ f(1,m) $肯定是最大价值，那么我们便开始考虑能
否选取第1个物品呢。
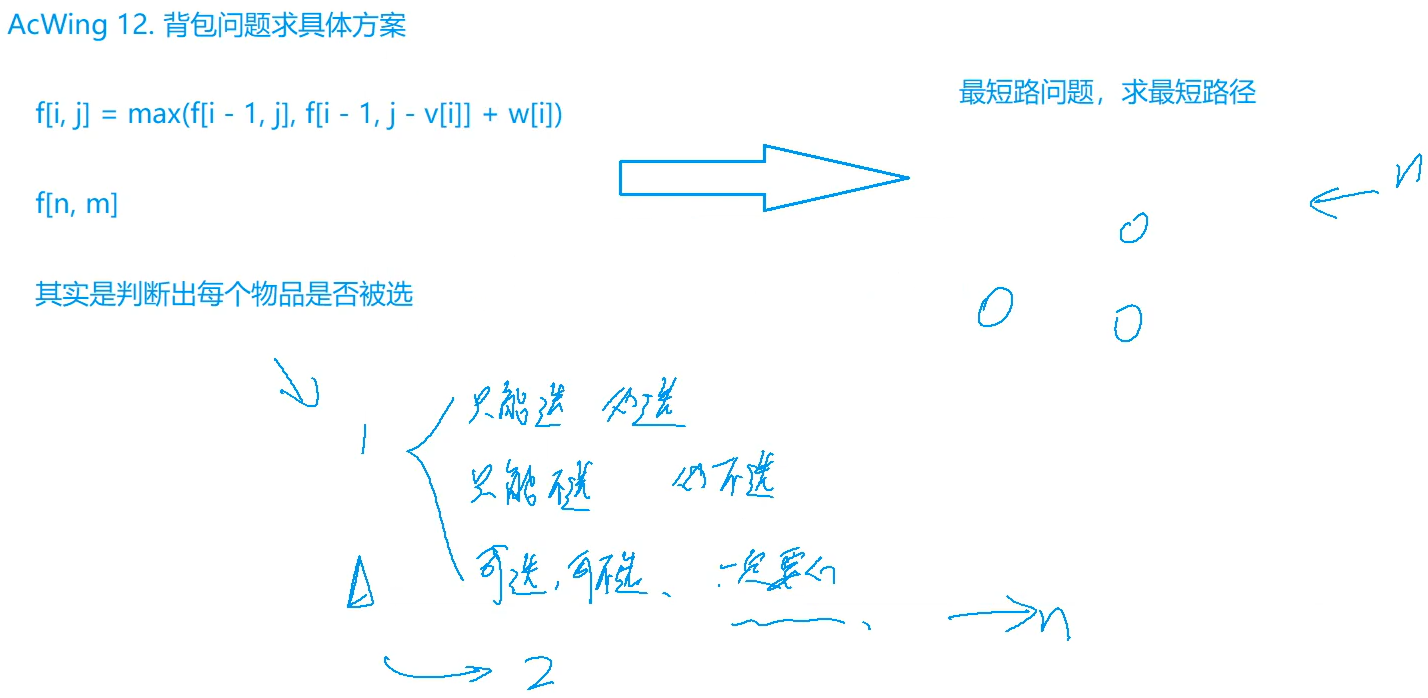
如果$f(1,m) = f(2,m-v[1])+w[1]$,说明选取了第1个物品可以得到最优解。
如果$f(1,m) = f(2,m)$,说明不选取第一个物品才能得到最优解。
如果$f(1,m) = f(2,m)=f(2,m一v[1])+w[1]$,说明选不选都可以得到最优解，但是为了考虑字典
序最小，我们也需要选取该物品。

作者:@T-SHLoRk

原题解Link