《算法提高课》题解与笔记上线啦！(链接就是这个){: style=”color: #FF0000”}

创建时间2024-1-24

$$ #6 1020.潜水员 $$

二维费用背包模型(最小值)

原题Link

扩展

可能很多人会有这样的疑问，二维费用的背包问题的状态转移方程代码如下

for(int j =  V;j >= v;j --)
    for(int k = M;k >= m;k --)
        f[j][k] = max(f[j][k], f[j - v][k - m] + w);

而本题的状态转移方程代码如下

for(int j = V;j >= 0;j --)
    for(int k = M;k >= 0;k --)
        f[j][k] = min(f[j][k], f[max(0, j - v)][max(0, k - m)] + w);

为什么上面的代码 j只需要遍历到v，k只能遍历到m。而下面的代码 j还需要遍历到0，k还需要遍历到0 ？同时为什么氧气或者氮气所需的是数量是负数时，可以与数量0的状态等价？

解答：

对比两题的思路，二维费用的背包问题，求的是不能超过体积V，重量M的情况下，能拿到价值的最大值。而本题是至少需要体积V，重量M的情况下，能拿到价值的最小值。就拿体积来说，至少需要多少体积，也就是说有体积比需要的体积大的物品还是能用得到，例如f[3][5]，至少需要3个体积，5个重量，求能拿到价值的最小值，现在只有一个物品，体积是4，重量是4，价值w，它说至少需要3个体积，那么体积是4还是可以用到，只是多了1个体积没用占着而已，不影响其价值。因此若用了这个物品，则变成了求f[0][1] + w，表示体积已经不再需求了，只需要0个体积即可

作者：@小呆呆

原题解:Link

Code:

# include <bits/stdc++.h>
using namespace std;

const int M = 30, N = 90;

int m, n, k, v1, v2, w;
int f[M][N];

int main(){
    scanf("%d %d %d", &m, &n, &k);
    memset(f, 0x3f, sizeof f); // 求最小值要初始化为正无穷
    f[0][0] = 0;

    while(k --){
        scanf("%d %d %d", &v1, &v2, &w); // 一个个输入更好
        for(int i = m; i >= 0; i --)
            for(int j = n; j >= 0; j --)
                f[i][j] = min(f[i][j], f[max(0, i - v1)][max(j - v2, 0)] + w); // i, j可以是负数，但是负数就等价于0，详见https://www.acwing.com/solution/content/7438/
    }

    printf("%d", f[m][n]);

    return 0;
}

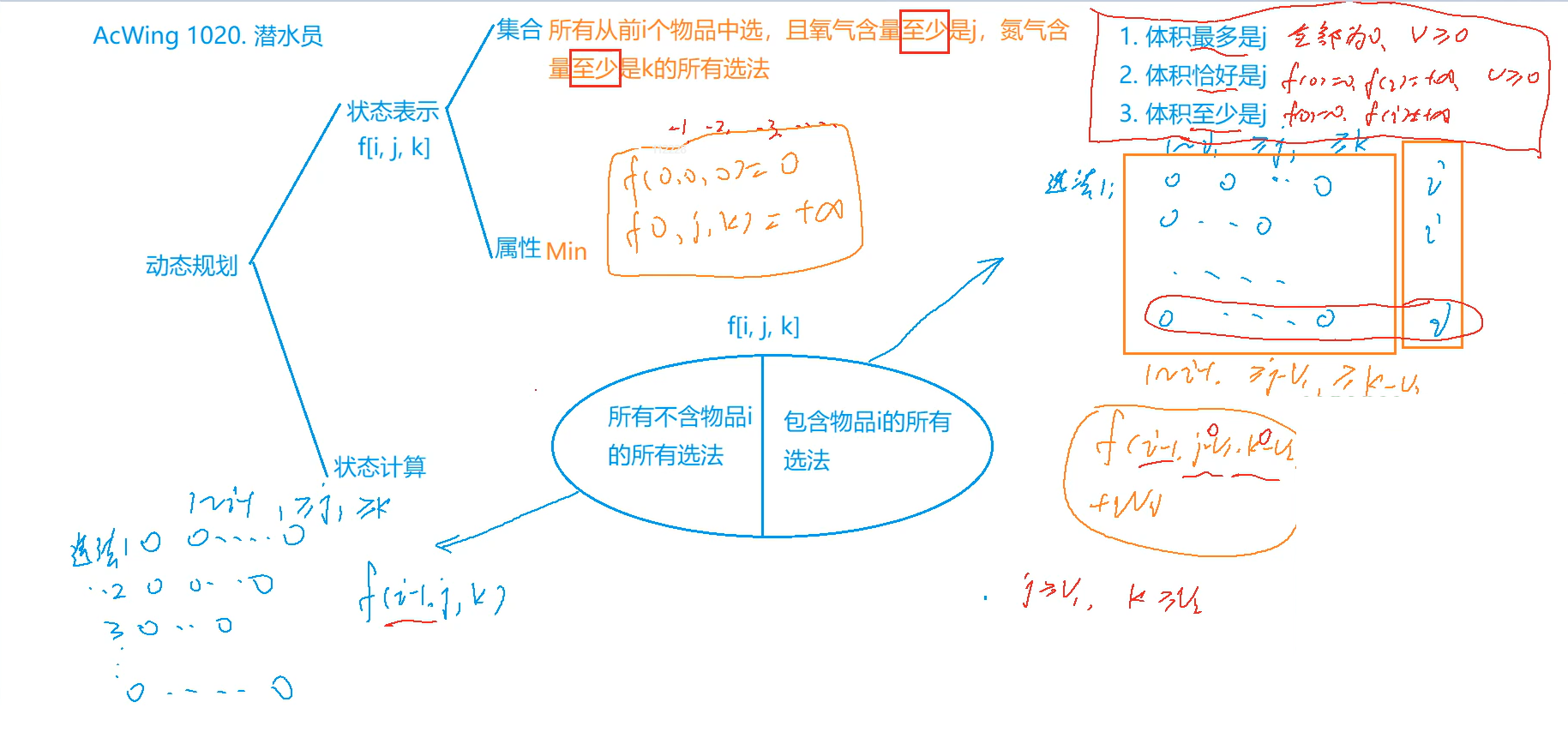
思路