枚举

递归实现指数型枚举

从 1~n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

const int N=15;
int n;
int st[N]; 
void dfs(int u)
{
    if(u>=n)
    {
        for(int i=0;i<=n;i++)
        {
            if(st[i]==1)printf("%d ",(i+1));
        }
       printf("\n");
       return;
    }
    st[u]=1;
    dfs(u+1);

    st[u]=2;
    dfs(u+1);
    st[u]=0;
}

递归实现排列型枚举

把 1~n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

const int N=10;
int n;
int state[N];//表示没用过，1~N表示数字
bool used[N];//true表示用过，false表示没用过

void dfs(int num)
{
     if(num>n)
     {
         for(int i=1;i<=n;i++) printf("%d ",state[i]);
         puts(" ");

         return;
     }
     for(int i=1;i<=n;i++)
     {
         if(!used[i])
         {
             used[i]=true;
             state[num]=i;
             dfs(num+1);

             state[num]=0;
             used[i]=false;
         }
     } 
}

递归实现组合型枚举

从 1~n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

const int N=30;
int n,m;
int way[N];
void dfs(int u,int start)
{
    if(u==m+1)
    {
        for(int i=1;i<=m;i++)printf("%d ",way[i]);
        puts("");
        return;
    }
    for(int i=start;i<=n;i++)
    {
        way[u]=i;
        dfs(u+1,i+1);
    }
}

二分法

整数的二分法

样题链接
https://www.acwing.com/problem/content/submission/code_detail/1524544/

算法模板
```
// n 是数组的中元素的个数
// k为要查找的数
//输出为该元素的起始位置与终止位置
int l = 0, r = n -1;
int k;
scanf(“%d”,&k);
while(l < r)
{
int mid = l + r >> 1;
if(m[mid] >= k)r = mid;
else l = mid + 1;
}

    if(m[l] != k) printf("-1 -1\n");
    else
    {
        cout << l << ' ';

        int l = 0, r = n - 1;
        while(l < r)
        {
        int mid = l + r + 1 >> 1;
        if(m[mid] <= k)l = mid;
        else r = mid - 1;
        }
        cout<<l<<endl;
    }

```

double类型的二分法

 while(r-l>1e-8)
    {
        mid = (l + r)/2;
        if(mid*mid*mid > n)r = mid;
        else l = mid;
    }

前缀和

一维前缀和

1，初始化数组

    for(int i = 1;i <= n;i++)
    {
        s[i] +=s[i-1];
    }

2, 求和

    while(m--)
    {
        res = s[r]-s[l-1];
    }

二维数组前缀和

1，初始化数组

    for(int i = 1;i <=n;i++)
    for(int j = 1;j <=m;j++)
    {
    s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];
    }

2, 求和

   for(int i =0;i<q;i++)
    {
        res = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
        cout<<res<<endl;
    }

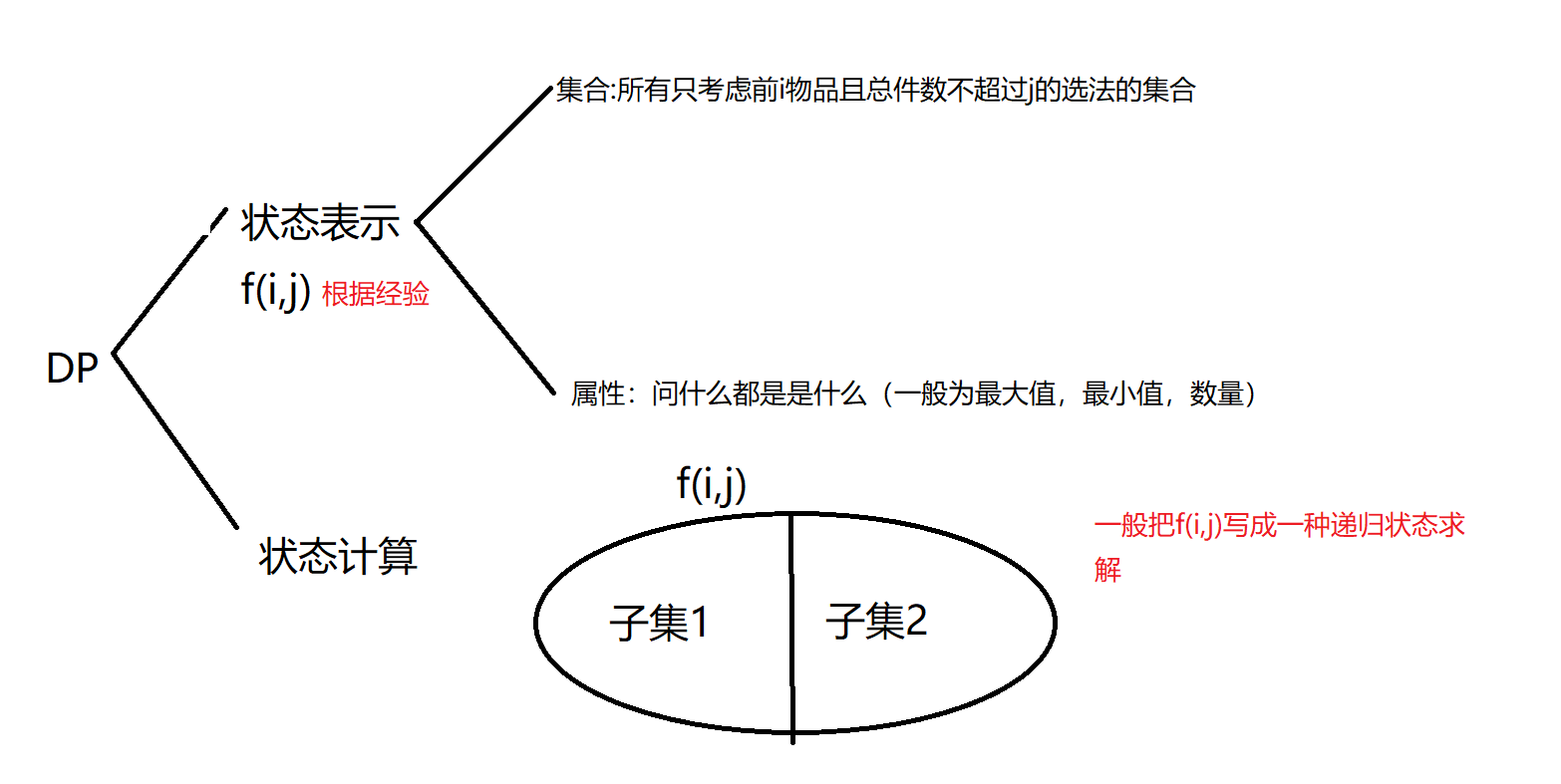
闫式DP

总的来说，我感觉DP方法主要还是靠经验。我是菜鸡就不过多总结了。只是把y总的模板放在这里。

双指针算法

算法思想： 利用问题本身与序列的特性（序列递增性质），使用两个下标i、j对序列进行扫描 （可以同向扫描，也可以反向扫描） ，以较低的复杂度解决问题。

for(int i = 0,j = 0;i < n;i++)
   {
      while()
       {
           j++;
       }
   }

DFS

dfs()
{  
    if(到达终点状态)  
    {  
        ...//根据题意添加  
        return;  
    }  
    if(越界或者是不合法状态)  
        return;  
    if(特殊状态)//剪枝
        return ;
    for(扩展方式)  
    {  
        if(扩展方式所达到状态合法)  
        {  
            修改操作;//根据题意来添加  
            标记；  
            dfs（）；  
            (还原标记)；  
            //是否还原标记根据题意  
            //如果加上（还原标记）就是 回溯法  
        }  

    }  
}

BFS

void bfs ()
{
    queue 初始化

    while(hh <= tt)  //队列非空
    {
        t = q[hh ++ ];  //更新队头

        // 扩展队头 + 放入队列
    }
}

欧几里得算法

int gcd(int a,int b)
{
    return b ? gcd(b,a%b) : a;
}

预处理质数

void get_primes(int n)  //预处理质数
{
    for(int i = 2;i<=n;i++)
    {
        if(!st[i])
        {
            minp[i] = i;
            primes[cnt++] = i;
        }

        for(int j = 0;primes[j]*i<= n;j++)
        {
            int t =primes[j]*i;
            st[t] =true;
            minp[t] = primes[j];
            if(i%primes[j]==0)break;
        }
    }
}