AcWing《算法提高课》第1章 动态规划

更新说明

目前只更新了动态规划的数字三角形模型

剩下的随缘更新

剩下的等做好了再放上来

动态规划知识点

闫氏思考法：从集合的角度考虑动态规划问题

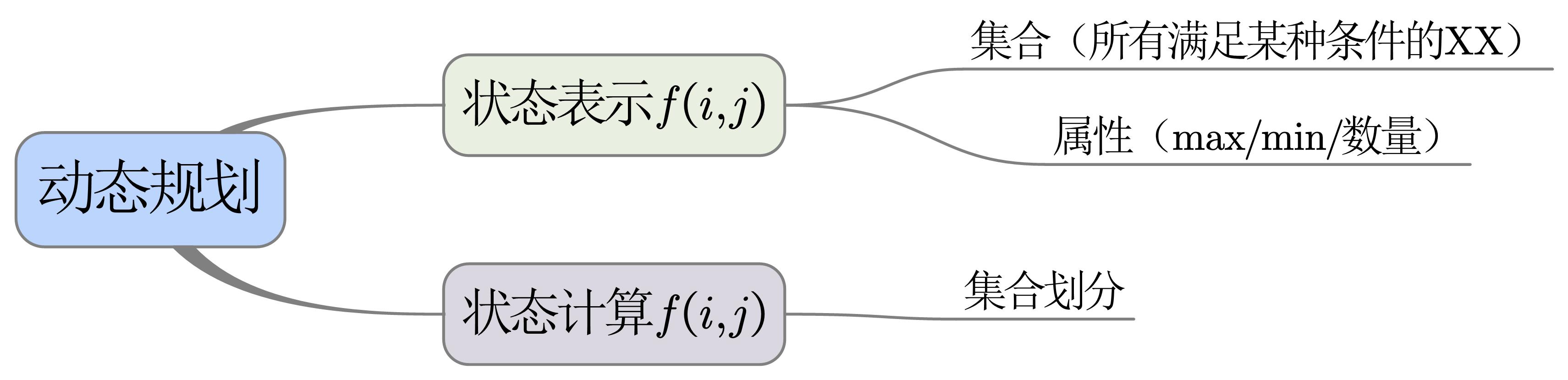{:height=”75%” width=”75%”}

常见划分依据：最后

• 最后一步是从上边来的 $f(i-1,j)+w(i,j)→f(i,j)$
• 最后一步是从左边来的$f(i,j-1)+w(i,j)→f(i,j)$

集合划分原则

• 不重复（仅约束属性是数量的情况，$\max$和$\min$允许划分的集合之间有重复，例如最长公共子序列）
• 不遗漏（所有属性都约束）

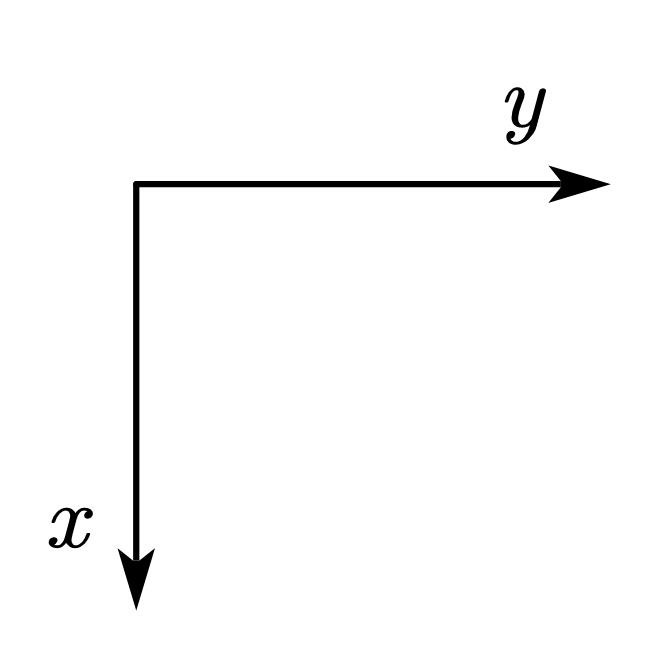
算法中的坐标系

算法中的坐标系并不是数学中定义的坐标系，而是如下图所示的坐标系

{:height=”30%” width=”30%”}

与暴力搜索的区别

暴搜每次只能处理一种情况，因此效率低下；而动态规划的一个状态包含了若干种情况，是满足某个条件的情况集合，每次状态转移就能涉及若干情况，因此效率更高

数字三角形模型

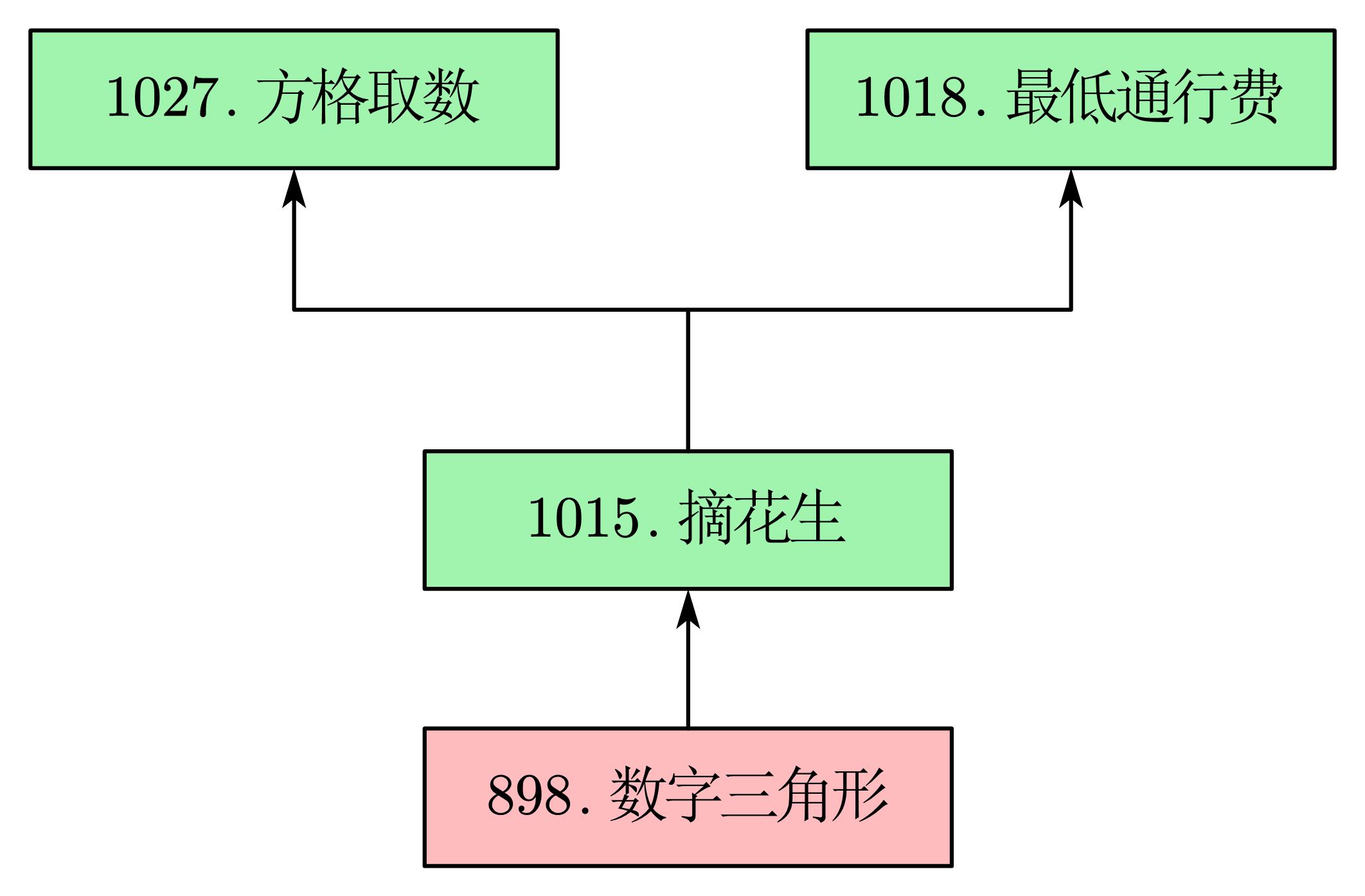{:height=”50%” width=”50%”}

模型回顾

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

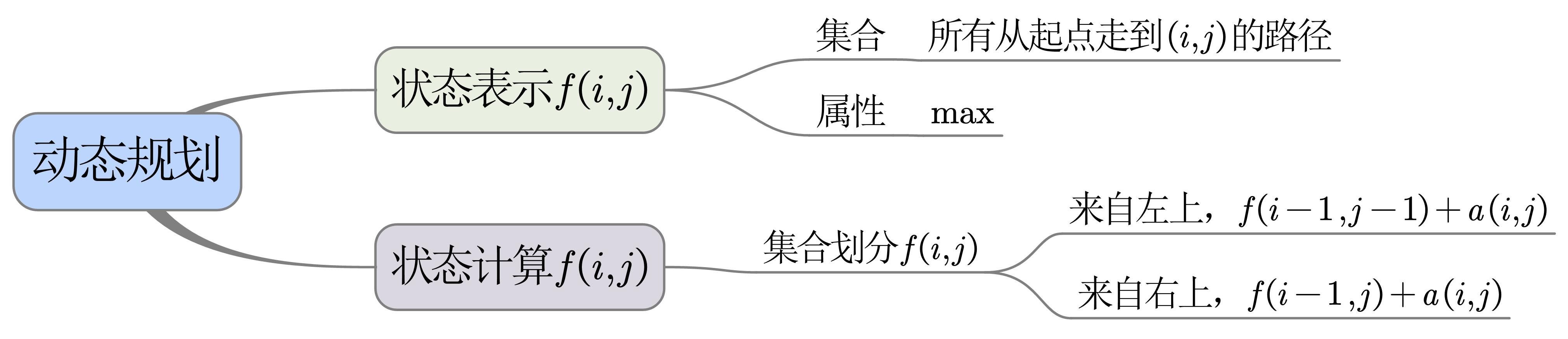{:height=”75%” width=”75%”}

核心代码

// 自顶向下（未压缩f)
const int INF = 1e9;

for (int i = 0; i <= n; i ++ )
    for (int j = 0; j <= i + 1; j ++ )
        f[i][j] = -INF;

f[1][1] = a[1][1];
    for (int i = 2; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);

int res = -INF;
for (int j = 1; j <= n; j ++ ) res = max(res, f[n][j]);

摘花生

题意

网格各顶点有给定数量的花生，找一条从左上角到右下角的路径，使得路径上的花生数量之和最大。每次只能向右或向下走。

思路

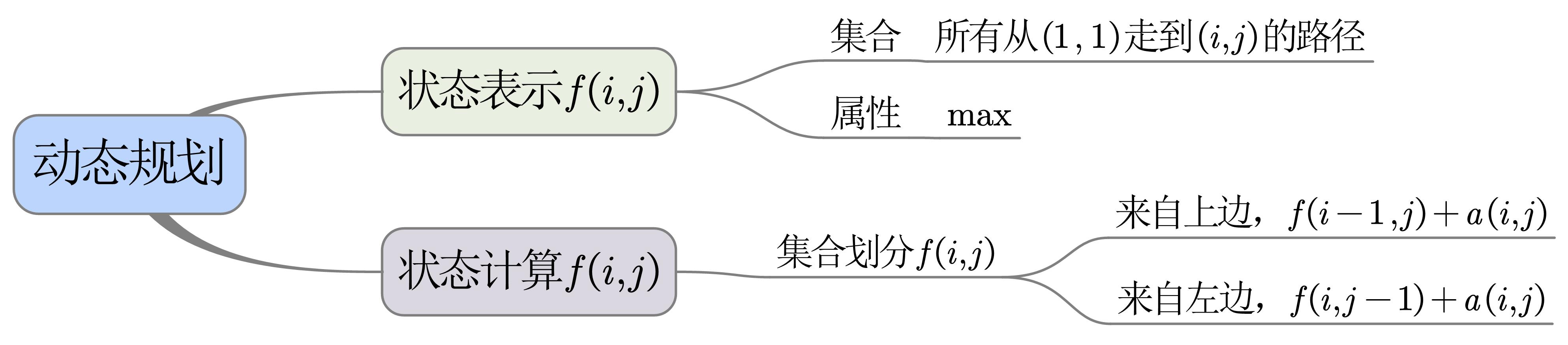{:height=”75%” width=”75%”}

核心代码

for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++ )
        f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];      // max后才加w[i][j]不会影响max的选取

printf("%d\n", f[n][m]);

笔记

• 根据最后一步的来源，即上一步的方向，可将$f(i,j)$划分成两个不重复且无交集的子集$f(i-1,j)$和$f(i,j-1)$
• 对比数字三角形模型
  • 一个是三角形，一个是矩形
  • 都只有两个方向可以走，且不能回头
  • 都是从左上角走到右下角
  • 都按照上一步的方向划分集合
  • 当前步与上一步只相差一个常数，满足线性关系（线性DP）
  • 都是求最大路径（最小路径也类似）

最低通行费

题意

从$n\times n$网格的左上走到右下，最多走$2n-1$次，即最多穿过$2n-1$个格子（包括起点和终点），求一条路径，使得经过的格子数值之和最小

思路

当$n=4$时，最多只能走$2n-1=7$次，下图为一种可行的示意图，实际上当只能向下或向右走时，穿过的格子数恰好是$2n-1$。在只能往上下左右四个方向走的限制下，这是最少穿过的格子总数（可以往曼哈顿距离考虑）。

{:height=”30%” width=”30%”}

因此“最多走$2n-1$次”$\Rightarrow$只能向右或向下走。故此问题转变成类似摘花生的问题，但二者仍有一些差异。

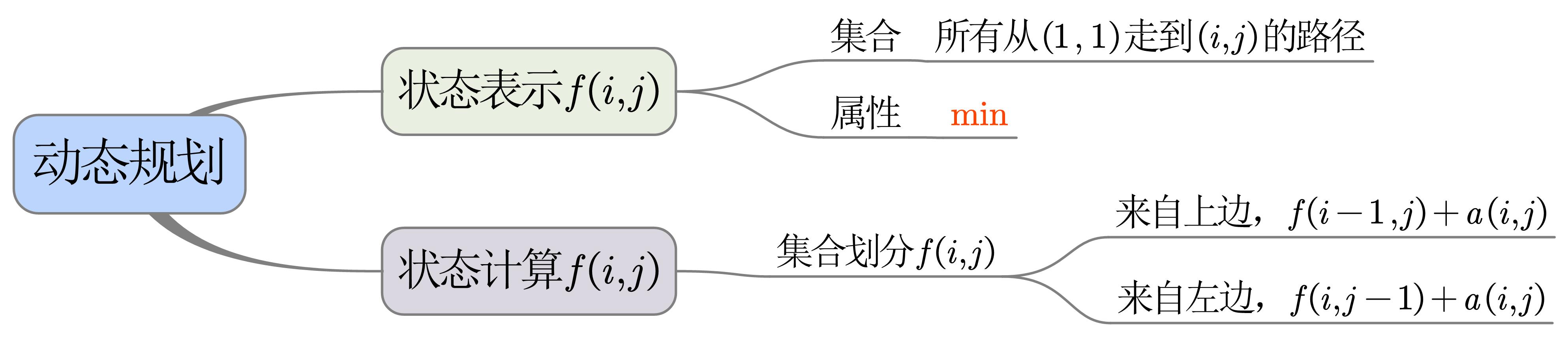{:height=”75%” width=”75%”}

二者的主要差异：本题求的是最小路径，而摘花生求的是最大路径。这个差别在代码上体现为矩阵f边界(i==0和j==0)初值的选取

• 摘花生问题中，花生数量是正数，边界默认初值为0时，不影响max的选取；
• 而最低通行费问题中，如果边界初值是0，且网格的值是正数，则会影响min的选取，因此边界应当初始化为无穷大，例如0x7f7f7f7f。

当把矩阵f初值设为无穷大后，需要单独对f[1][1]处理，它的值应当为a[1][1]，可在二重循环内单独用if(i==1 && j==1)处理，否则f[1][1]会受$\infty$影响变成$\infty + a[1][1]$而出错。

当然也可以把f[0][1]或f[1][0]置为0，使得f[1][1] = min(f[0][1], f[0][1]) + a[1][1] = 0 + a[1][1] = a[1][1]就行，这样有个好处，循环内部不用特判，代码简洁。

{:height=”30%” width=”30%”}

核心代码

memset(f, 0x7f, sizeof f);

f[0][1] = 0;        // 也可换成f[1][0] = 0 
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++)
        f[i][j] = min(f[i-1][j], f[i][j-1]) + a[i][j];

cout << f[n][n] << endl;

注：我没有采用y总的代码实现，虽然比较好想，但感觉代码太复杂…

方格取数

题意：在$n\times n$网格选两条从左上角到右下角的路径，使得二者之和最大（路径相交的格子只计一次）

思路

可以用两组坐标，即4个参数表示两条路径的状态，由于每条路径是独立的，且只能往下或往右走，故可划分为4类，如下图所示。

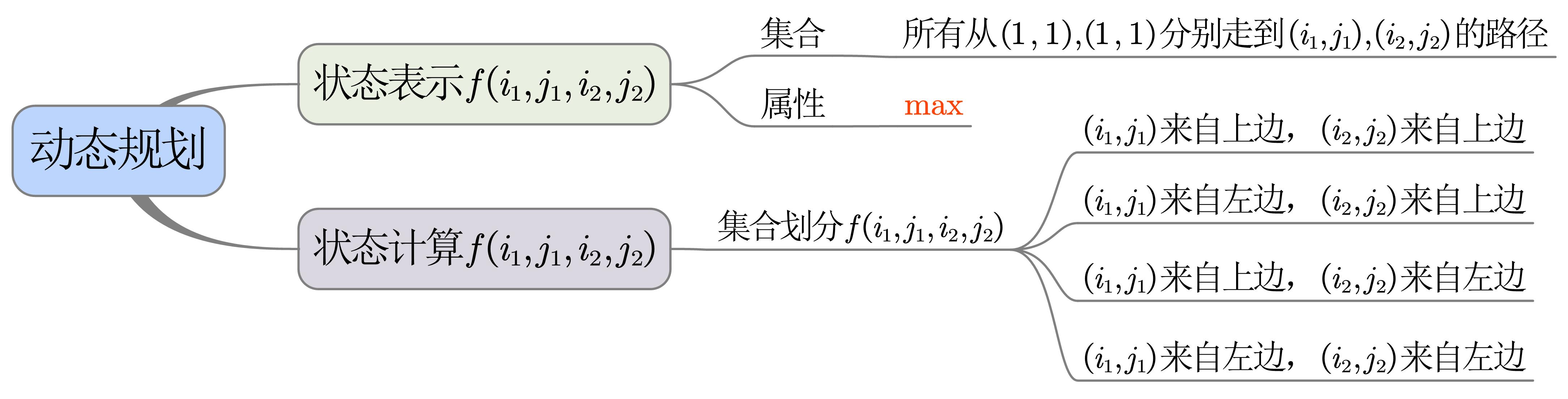
当两条路径的横纵坐标之和相等时，才可能在当前位置相交，此时满足$i_1+j_1=i_2+j_2$。

若令$i_1+j_1=i_2+j_2=k$，则只用3个参数$i_1,j_1,k$就能表示$i_1,j_1,i_2,j_2$，其中$j_1=k-i_1$，$j_2=k-i_2$。$k$既表示从$(1,1)$到$(i_1,j_1)$的横纵坐标之和，又表示从$(1,1)$到$(i_2,j_2)$的横纵坐标之和。当$k$不变时，若$i_1=i_2$，则$j_1=j_2$，即两条路径相交于$(i_1,j_1)$。

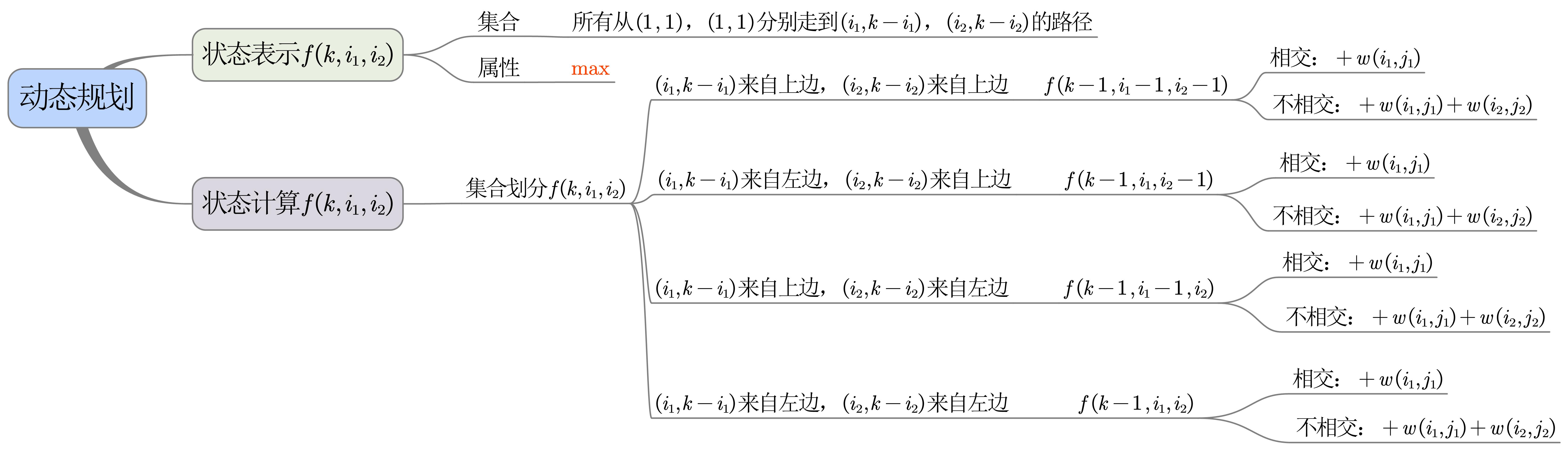
核心代码

int w[N][N];
int f[N * 2][N][N];     // k最大取2N

// main
for (int k = 2; k <= n + n; k ++ )
    for (int i1 = 1; i1 <= n; i1 ++ )
        for (int i2 = 1; i2 <= n; i2 ++ )
        {
            int j1 = k - i1, j2 = k - i2;
            if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
            {
                // 提前算好增量，减少代码量
                int t = w[i1][j1];                      // 相交时有w[i1][j1]==w[i2][j2]，只需记录一次
                if (i1 != i2) t += w[i2][j2];           // 若不相交，则还要记录w[i2][j2]

                int &x = f[k][i1][i2];                  // 用x表示f[k][i1][i2]，减少代码长度
                x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);       // 第1条路径来自上边，第2条路径来自上边
                x = max(x, f[k - 1][i1 - 1][i2] + t);           // 第1条路径来自上边，第2条路径来自左边
                x = max(x, f[k - 1][i1][i2 - 1] + t);           // 第1条路径来自左边，第2条路径来自上边
                x = max(x, f[k - 1][i1][i2] + t);               // 第1条路径来自左边，第2条路径来自左边
            }
        }

printf("%d\n", f[n + n][n][n]);

说明

• 由于是最大路径，且格子上的数是非负数，故矩阵f可以使用默认值0初始化