静态链表

int head,e[N],ne[N],idx;
//head为记录头结点
//e[N]记录每个单链表的值
//ne[N]记录每个链表next指针
//idx 记录总共值的个数

//初始化单链表
void init()
{
    head = -1;
}

//在头结点加入一个值
void add_head(int x)
{
    e[idx] = x,ne[idx] = head,head = idx++;
}


//表示在第k个输入的数后面插入一个数x
void add_k(int k,int x)
{
    e[idx] = x,ne[idx]=ne[k],ne[k]=idx++;
}


//表示删除第k个输入的数后面的数
void remove(int k)
{
    ne[k] = ne[ne[k]];
}

//遍历链表的方法
for(int i = head;i!= - 1;i = ne[i])cout <<e[i]<<' ';
cout<<endl;

静态链表记录树和图

主要思想是用把树或者是图用临界链表的方式存储，之后把临界链表改写成静态链表的方式。其中h[N]中记录这每一个头结点的位置

const int N = 100010, M = N * 2;

int n;
int h[N], e[M], ne[M], idx;
int ans = N;
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}


//主函数初始化过程
//其中a和b表示两点之间有一条边
memset(h, -1, sizeof h);

for (int i = 0; i < n - 1; i ++ )
{
     int a, b;
     scanf("%d%d", &a, &b);
     add(a, b), add(b, a);
}

线段树和树状数组

应用背景：给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。
线段树和树状数组与前缀和都是求一个区间上的的和。如果不进行修改元素的操作，前缀和可以把复杂度降低到O(1)。
但是如果存在修改元素的操作，前缀和算法复杂度就会升到O(n)。而线段树和树状数组允许修改操作，时间复杂度为O(logn)。

树状数组

模板题目链接https://www.acwing.com/problem/content/description/1266/

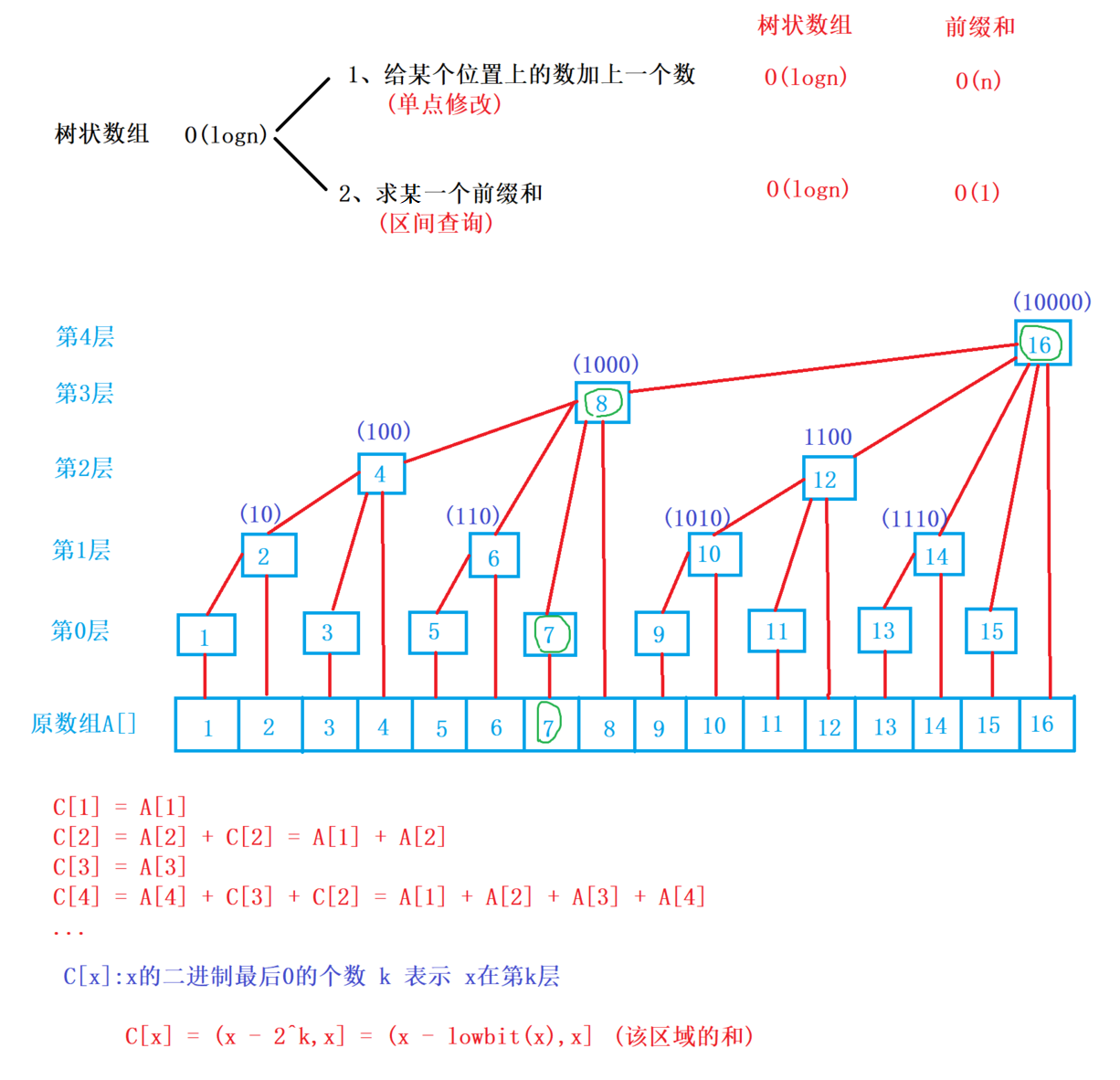
图片来自小呆呆同学的题解。
原题解的链接如下
https://www.acwing.com/solution/content/7526/
1、lowbit(x):返回x的最后一位1

int lowbit(int x)
{
    return x&-x;
}

2、add(x,v):在x位置加上v，并将后面相关联的位置也加上v

void add(int x,int v)
{
    for(int i = x;i<=n;i +=lowbit(i)) tr[i] +=v;
}

3、query(x):询问x的前缀和`

int query(int x)
{
    int res = 0;
    for(int i = x;i;i-=lowbit(i)) res += tr[i];
    return res;
}

线段树

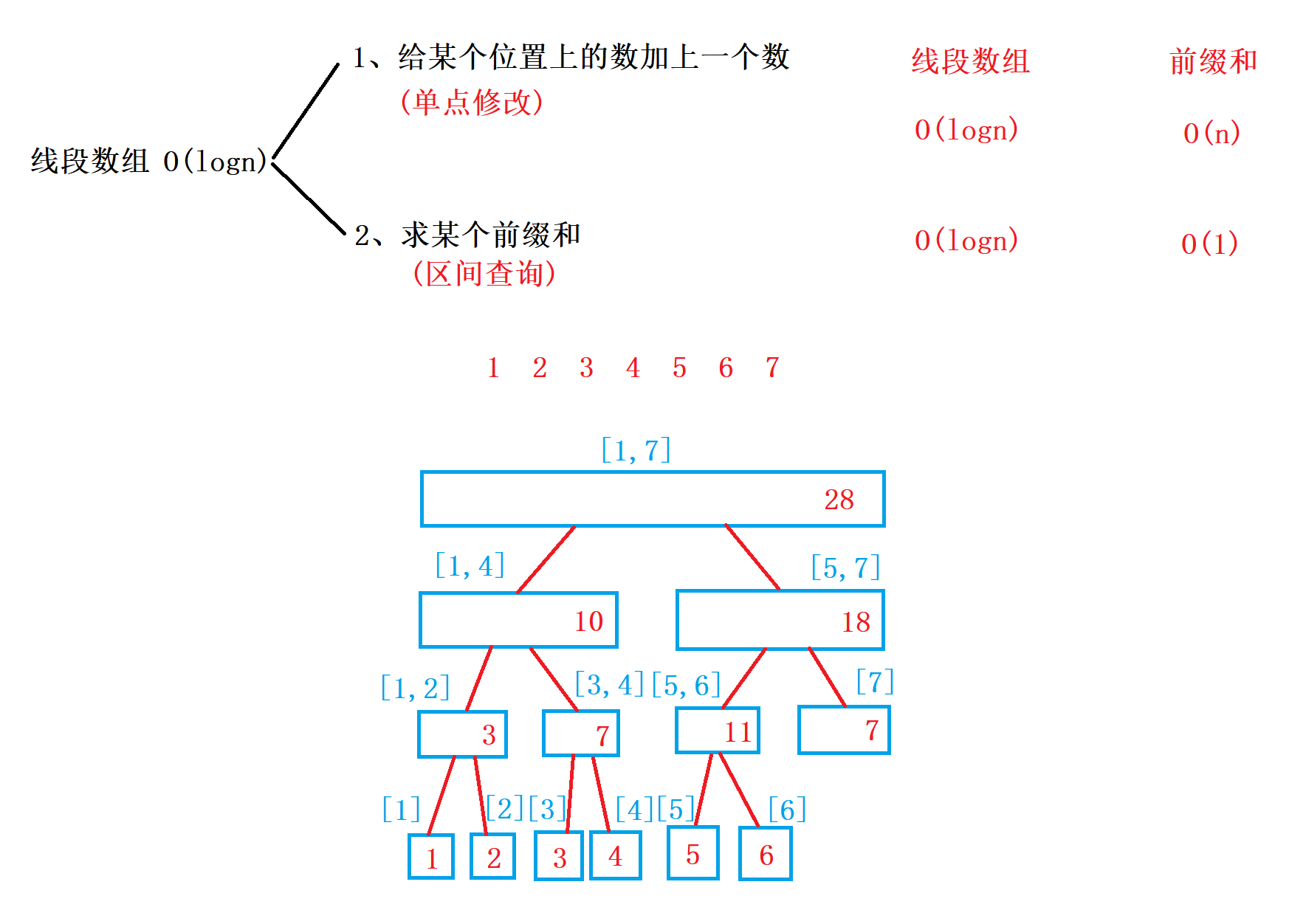
1、pushup(u):用子节点信息来更新当前节点信息（把信息往上传递）

void pushup(int u)
{
    tr[u].maxv = max(tr[u<<1].maxv , tr[u<<1|1].maxv);
}

2、build(u,l,r):在一段区间上初始化线段树，其中u表示根结点，l表示左边界，r表示右边界

void build(int u ,int l,int r)
{
    if(l == r)tr[u]={l,r,w[r]};
    else
    {
    tr[u] = {l,r};
    int mid = l + r >> 1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
    pushup(u);
    }
}

3、query(u,l,r):查询某段区间的和，其中u表示根结点，l表示左边界，r表示右边界

int query(int u,int l,int r)
{
    if(tr[u].l>=l && tr[u].r<=r)return tr[u].maxv;
    int res = INT_MIN;
    int mid = tr[u].l + tr[u].r >> 1;
    if(mid>=l)res = query(u<<1,l,r);
    if(mid<r)res = max(res,query(u<<1|1,l,r));
    return res;
}

4、modify(u,x,v):修改操作，在u结点中，x位置加上v

   void modify(int u,int x,int v)
    {
        if(tr[u].l == tr[u].r) tr[u].sum += v;
        else
        {
            int mid = tr[u].l + tr[u].r >> 1;
            if(x <= mid) modify(u << 1,x,v);
            else modify(u << 1 | 1,x,v);
            pushup(u);
        }
    }

堆

堆（英语：heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：
1. 堆中某个节点的值总是不大于或不小于其父节点的值；
2.堆总是一棵完全二叉树。
3.将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的up和down操作

down

void down(int u)
{

    int t = u ;
    if(2*u <= cnt && h[2*u]<h[t]) t = 2*u;
    if(2*u + 1 <=cnt && h[2*u+1]<h[t]) t =2*u + 1;

    if(t != u)
    {
        swap(h[t],h[u]);
        down(t);
    }
}

up

void up(int u)
{
    while(u/2 && h[u/2] > h[u])
    {
        swap(h[u/2],h[u]);
        u /= 2;
    }
}

堆的五个基本操作

1.插入一个数

heap[++size] = x;up(size);

2.求集合当中的最小(大)值

heap[1]; 

3.删除最小值

heap[1] = heap[size];size--;down(1);

4.删除任意一个元素

heap[k] = heap[size];size--;down(k);up(k);

5.修改任意一个操作

heap[k] = x;down(k);up[k];