AcWing《算法基础课》第1章 算法基础
排序
快速排序
主要思想:
- 确定分界点:
x = a[l]x = a[r]q = a[(l + r) / 2]
- 调整范围:
- 左边
<=x - 右边
>x
- 左边
- 递归处理左边和右边
模板:
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x); // 可换成 while(q[ ++ i ] < x);
do j -- ; while (q[j] > x); // 可换成 while(q[ -- j ] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
quick_sort(a, 0, n - 1); // 调用方法
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l];
while (i < j)
{
do i ++ ; while (q[i] < x); // 可换成 while(q[ ++ i ] < x);
do j -- ; while (q[j] > x); // 可换成 while(q[ -- j ] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
quick_sort(a, 0, n - 1); // 调用方法
说明:
如果x选取q[l],则递归时参数范围选择(l, j)和(j + 1, r)
如果x选取q[r],则递归时参数范围选择(l, i - 1)和(i, r)
如果x选取q[l + r >> 1],则递归时参数范围选择哪种都行
证明:
反例:
如果算法x选取q[l],即x = q[0] = 1,递归时参数范围选择(l, i - 1)和(i, r),则下一次迭代后i = 0,j = 0,递归时参数的范围为(0, -1)和(0, 1),其中第1个递归无效,第2个递归与之前一致,陷入死循环。
同理如果算法x选取q[r],即x = q[1] = 2,递归时参数范围选择(l, j)和(j + 1, r),则下一次迭代后i = 1,j = 1,递归时参数的范围为(0, 1)和(2, 1),其中第2个递归无效,第1个递归与之前一致,陷入死循环。
注意:
快速排序在对含有重复元素的数组排序时是不稳定的,但可以把元素值和其下标组成二元组{q[i], i}后再排序,这样就能使排序结果稳定。
应用:
归并排序
主要思想:
- 确定分界点
mid = (l + r) / 2 - 递归处理左右两段
- 归并(双指针算法,指针表示剩余部分中最小元素的位置)
模板:
int tmp[N]; // 归并步骤用
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ];
while (j <= r) tmp[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
merge_sort(a, 0, n - 1); // 调用方法
注意:
在归并步骤时,如果碰到相同元素的插入,每次都选择第1段(左边)的元素插入,则能使归并算法稳定。
应用:
二分
整数二分
模板:
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 寻找左半边边界
int bsearch_left(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1; // 让下取整变成上取整,避免l = mid出现死循环
if (check(mid)) l = mid; // a[mid]满足左半边性质,应在[mid, r]继续寻找
else r = mid - 1; // a[mid]不满足左半边性质,应在[l, mid - 1]继续寻找
}
return l; // 二分结束后,l == r。如果一定存在左半边的边界,l和r都是结果。如果不一定存在左半边的边界,需要做if判断
}
// 寻找右半边边界
int bsearch_right(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // a[mid]满足右半边性质,应在[l, mid]继续寻找
else l = mid + 1; // a[mid]不满足右半边性质,应在[mid + 1, r]继续寻找
}
return l; // 二分结束后,l == r。如果一定存在右半边的边界,l和r都是结果。如果不一定存在右半边的边界,需要做if判断
}
个人理解:
二分的本质是寻找边界:如果一组数能根据某个性质一分为二,则可快速通过二分找到边界。它有两种模板:寻找左半边的边界和右半边的边界。
寻找左半边边界需要+1的原因:当l和r只相差1,即l == r - 1时。mid = (l + r) / 2 = l。若此时a[mid]满足左边边性质,则有(l, r)→(mid, r)=(l, r),搜索区间不变,则陷入死循环。若+1,则下取整变成上取整,此时mid = (l + r + 1) / 2 = r。若此时a[mid]满足左边边性质,则有(l, r)→(mid, r)=(r, r),则结果为r,不会陷入死循环。
实际运用时,先不考虑用哪个模板,而是先写check()函数,然后写模板(不考虑mid是否+1),写到if(check(mid))时,再考虑满足check(mid)的段是在哪一边:如果在左边,则填l = mid;如果在右边,则填r = mid。然后填出else的部分,如果存在l = mid,则要在mid声明处+1;反之不补。
说明:
- 整数二分不仅仅适用单调性,只要存在某种性质能把序列分成连续的两段就可以,即
check()函数 - 二分与单调性没有必然关系:有单调性的题目一定可以二分;可以二分的题目,不一定要用单调性。
浮点数二分
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
说明:
- 浮点数二分不需要考虑
mid是否+1,else后是否+1。 - 没有固定的浮点数序列,因此要考虑精度
eps,一般比题目要求多1位小数就行 - 需要自己确定
l和r的值,即查找范围
应用:
高精度计算
大整数存储
模板:
vector<int> A;
string a;
cin >> a;
for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
**说明:
- 这里假设大整数是非负数
- 数组A中
0对应大整数的最低位(个位),n-1对应最高位
大整数比较
模板:
// A >= B返回true,否则返回false
bool cmp(vector<int>& A, vector<int>& B) {
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i--)
if (A[i] != B[i])
return A[i] > B[i];
return true;
}
高精度加法
模板:
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
说明:
- 模板假设
A和B都是非负大整数 - 假设大整数
A的位数≥大整数B,不满足要交换参数次序 - 大整数低位存放在数组低地址处,高位存放在数组高地址处
- 数组地址由低到高(
0→n - 1) - 整数位数最左边是高位,最右边是低位(高位→低位)
- 数组地址由低到高(
- 注意处理最高位进位
- 读取数组时反向(
n-1→0)遍历,运算时正向(0→n-1)遍历 - 高精度加法不会出现前导
0,而减法、乘法和除法会出现前导0
| 数组下标 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 存储数 | 5 | 6 | 7 | 8 | - |
| 原数 | 8 | 7 | 6 | 5 | - |
高精度减法
模板:
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10); // 涵盖t为正数负数两种情况
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); // 去掉前导0,但不能把结果`0`去掉
return C;
}
说明:
- 模板假设
A和B都是非负大整数,且A≥B,可用cmp()模板判断是否满足A≥B,不满足交换参数次序即可 (t + 10) % 10涵盖了t正负两种情况t >= 0输出t % 10t < 0输出t + 10
- 减法会产生多个前导
0 - 去掉前导
0时,注意不能把结果0也去掉,即需要判断C.size() > 1
高精度乘法
模板:
// C = A * b, A >= 0, b > 0
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
说明:
- 模板假设
A是非负大整数,b是基本类型int - 乘法模板把对最高位的进位的处理翻到了
for的循环条件中,这是与加法的主要区别。加法之所以能用一个if就能解决最高位的进位问题,是因为高精度加法最高位进位不会超过10(实际上最多是1),而高精度乘法的最高位进位可能超过10,甚至更高,因此不能像加法那样处理
高精度除法
模板:
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end()); // #include <algorithm>
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
说明:
- 模板假设
A是非负大整数,b是基本类型int - 商用
vector<int>保存,余数用参数r保存 - 除法是反向遍历(高位到低位)
- 结果要翻转,注意导入
<algorithm>库 - 注意遍历时,
r = r * 10 + A[i];是=,而不是+=
前缀和
一维前缀和
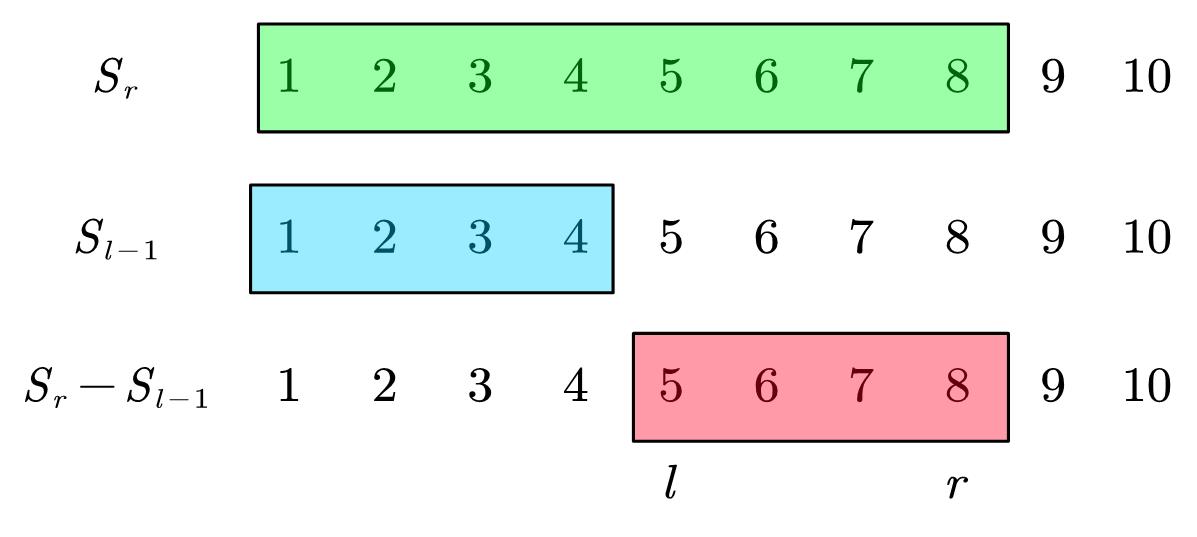
定义:
Sk=k∑i=1aiS0=a0=0al+al+1+⋯+ar=Sr−Sl−1
示意图:
模板:
int a[N], S[N];
for (int i = 1; i <= n; i++) S[i] = S[i - 1] + a[i]; // 给定数组a,初始化前缀和数组S
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]) // 非必须
S[i] = S[i - 1] + a[i]; // 未给定数组a,可合并读入和初始化的过程
}
cout << S[r] - S[l - 1] << endl; // 计算a[l] + ... + a[r]
笔记:
- 假设S0=a0=0
- 复杂度由
O(n)降为O(1) - 数组
a和S的第1个元素都不存储(下标为0),而从第2个元素开始存储(下标为1) - 注意遍历范围是
1 ~ n - 在一些不涉及
a[i]的题目中,不必要存储a[i]的值,只需要存储S[i]就足够
二维前缀和
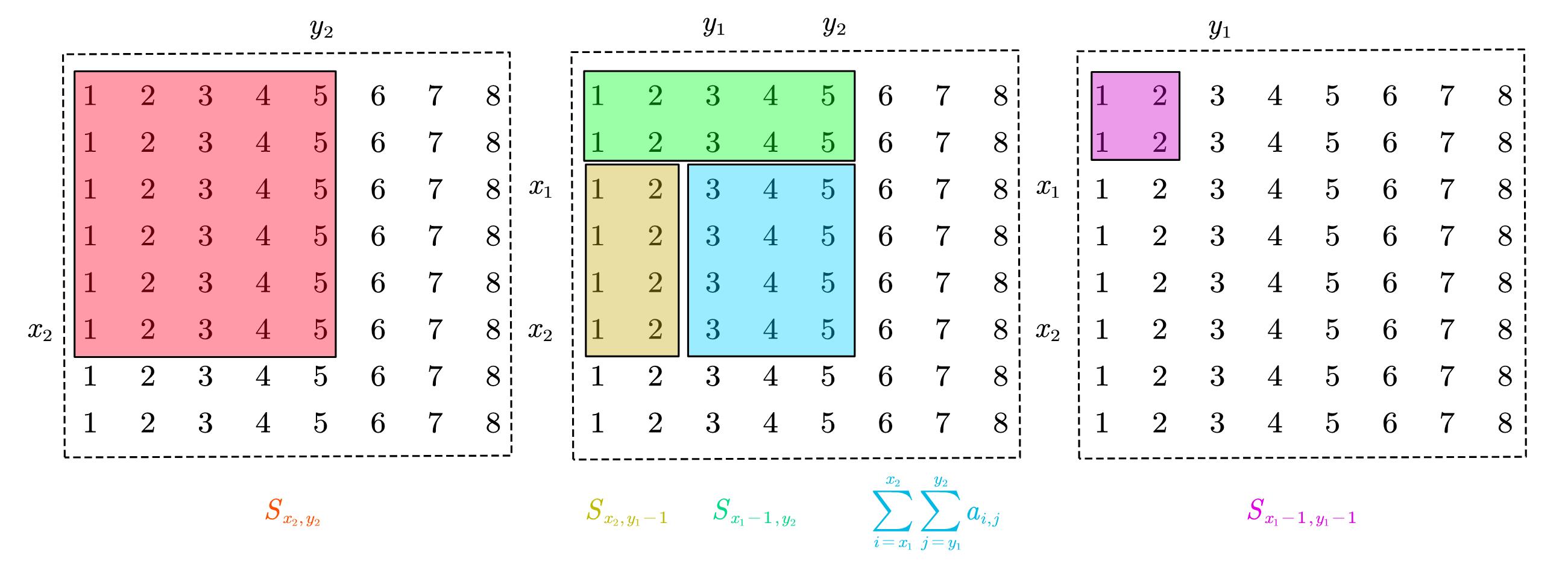
定义:
Sx,y=x∑i=1y∑j=1ai,j=Sx−1,y+Sx,y−1−Sx−1,y−1+ax,yS0,\*=S\*,0=a0,\*=a\*,0=0x2∑i=x1y2∑j=y1ai,j=Sx2,y2−Sx1−1,y2−Sx2,y1−1+Sx1−1,y1−1
示意图:
模板:
int a[N][N], S[N][N];
// 给定数组a
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j];
// 没有给定数组a,需要读入并初始化前缀和数组,则可以合并读入和初始化的过程
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j];
}
cout << S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2] + S[x1 - 1][y1 - 1] << endl; // 使用
说明:
- 假设数组
a中行下标或列下标为0的项都是0 - 复杂度由
O(m * n)降为O(1) - 读入数组
a和初始化前缀和数组S的过程可以合并在一起 - 注意遍历范围是
1 ~ n - 在一些不涉及
a[i][j]的题目中,不必要存储a[i][j]的值,只需要存储S[i][j]就足够
差分
一维差分
给区间[l,r]中的每个数加上c:
模板:
int a[N], B[N];
void insert(int l, int r, int c) {
B[l] += c;
B[r + 1] -= c;
}
// 初始化差分数组
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
insert(i, i, a[i]);
}
// 输出前缀和数组
for (int i = 1; i <= n; i++) {
B[i] += B[i - 1];
printf("%d ", B[i]);
}
说明:
- 复杂度由
O(n)降为O(1) - 用
insert(i, i, a[i])与B[i] = a[i]初始化差分数组的区别在于,前者构造的差分数组B[n]等于-B[n - 1],而后者等于0 - 读入数组
a和初始化差分数组B的过程可以合并在一起 - 注意遍历范围是
1 ~ n - 在一些不涉及
a[i]的题目中,不必要存储a[i]的值,只需要存储S[i]就足够
二维差分
给[x1,y1]与[x2,y2]构成的矩形范围内的每个数加上c:
模板:
int B[N][N]; // 二维差分数组
void insert(int x1, int y1, int x2, int y2, int c) {
B[x1][y1] += c;
B[x2 + 1][y1] -= c;
B[x1][y2 + 1] -= c;
B[x2 + 1][y2 + 1] += c;
}
// 构造(无需额外的数组a)
int tmp;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &tmp);
insert(i, j, i, j, tmp);
}
}
// 转换成二维前缀和数组
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
B[i][j] += B[i - 1][j] + B[i][j - 1] - B[i - 1][j - 1];
说明:
insert()函数规律- 下标出现
2的部分都+1 - 范围最大最小的
+=c,其它-=c
- 下标出现
- 复杂度由
O(m * n)降为O(1) - 注意遍历范围是
1 ~ n
双指针算法
定义:
- 第1类双指针算法:一个指针操作一个序列(归并排序的合并步骤)
- 第2类双指针算法:两个指针操作同一个序列(快速排序)
模板:
for (int i = 0, j = 0; i < n; i++) {
while (j < i && check(i, j)) j++;
// 题目逻辑
}
说明:
- 目的是把
O(n2)复杂度降为O(n) - 双指针算法会把序列分成
3段,理解各段的含义很重要(尤其第2段)- 第1段:
0~j - 1 - 第2段:
j~i - 第3段:
i + 1~n - 1
- 第1段:
应用:
位运算
要点:
x & -x返回最后1位1,例如101000返回1000x >> k && 1返回x右起第k位二进制数
模板:
// 返回最后1位1,例如101000返回1000
int lowbit(int x) {
return x & -x;
}
说明:
- 若让
x不停地减去最后1位1,直到变成0,做减法的次数就是x二进制表示的1的个数 - 可用
for(int k = 31; k >= 0; k--)把int转成二进制数
离散化
适用问题:
需要开辟长度很大的数组统计数据(109),但实际使用的元素个数很少(105)
模板:
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
说明:
- 实际上解决的是稀疏数组表示的问题,本质是映射问题
- 先把元素存储在
vector<int> alls中,排序去重后,再把值映射到长度较小的数组a中 - 通过二分查找
find(x)找到元素x在数组a的下标 - 排序去重后的
alls与数组a的相对顺序是一致的 - 二分查找是整数二分的特例
应用:
区间合并
适用问题:
把若干个区间合并成多个没有交集的区间。
模板:
typedef pair<int, int> PII;
// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
vector<PII> res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9; // 左端点最小值
for (auto seg : segs)
if (ed < seg.first)
{
if (st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
else ed = max(ed, seg.second);
if (st != -2e9) res.push_back({st, ed});
segs = res;
}
说明:
- 先按左端点排序,然后再合并
- 选取第2个区间时,可分为两大类情况
- 有交集(包括“包含”和“相交但不包含”两种情况)
- 无交集
- 对于有交集的情况,只需保留最大的右端点即可
- 对于无交集的情况,首先判断是否是空区间(
st == -2e9),非空则保存当前区间,并跳至下一个区间 - 由于循环内部是先发现新的无交集区间才保存当前指向的区间,因此在循环结束后,还需要单独保存当前区间(注意判断是否为空区间)


纠错:如果
x选取q[l+r>>1],递归时参数范围选择(l, i - 1)和(i, r)会引起死循环(大概
厉害,以后遇到不会的就从你这里找,哈哈
老哥牛逼啊。。。
整数二分个人理解那块,true或false对应的算法模板是不是写反了
爱了爱了
学习学习
%%%
这笔记做的可以可以
谢谢支持~
厉害厉害