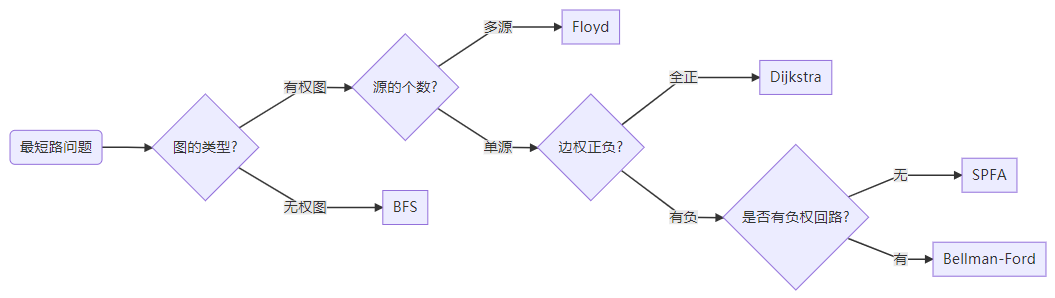
BFS

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int q[N], hh, tt = -1;
int d[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int bfs()
{
    // 初始化 d
    memset(d, -1, sizeof d);
    d[1] = 0;

    // 将顶点 1 作为第一层顶点放入队列
    q[++ tt] = 1;

    // 直到队列为 0，说明已遍历完所有顶点
    while (tt >= hh)
    {
        // 取出上一层的顶点 u
        int u = q[hh ++];

        // 访问 u 的所有邻接顶点 v
        for (int i = h[u]; i != -1; i = ne[i])
        {
            int v = e[i];

            // 如果 v 未被访问过
            if (d[v] == -1)
            {
                // 更新 d[v]
                d[v] = d[u] + 1;
                // 将 v 放到队列
                q[++ tt] = v;
            }
        }
    }
    return d[n];
}

int main()
{
    cin >> n >> m;
    // 初始化邻接表
    memset(h, -1, sizeof h);

    while (m --)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }

    cout << bfs() << endl;

    return 0;
}

Floyd

#include <iostream>
#include <cstring>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, k;
int d[N][N];

void floyd()
{
    // d[k][i][j]: 只经过点 1..k，从点 i 到点 j 的所有走法中，距离最近那一个
    // d[k][i][j] = d[k-1][i][k] + d[k-1][k][j]
    for (int k = 1; k <= n; k ++)
        for (int i = 1; i <= n; i ++)
            for (int j = 1; j <= n; j ++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main()
{
    cin >> n >> m >> k;
    // 初始化 d，负自环归零
    memset(d, 0x3f, sizeof d);
    for (int x = 1; x <= n; x ++) d[x][x] = 0;

    while (m --)
    {
        int a, b, w;
        cin >> a >> b >> w;
        // 只记录最小权边
        d[a][b] = min(d[a][b], w);
    }

    floyd();

    while (k --)
    {
        int a, b;
        cin >> a >> b;
        // 负权边会略微扰动，使得两个不连通的顶点间的d值偏低
        if (d[a][b] > INF / 2) puts("impossible");
        else cout << d[a][b] << endl;
    }

    return 0;
}

Dijkstra

朴素算法

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510;

int g[N][N];
int d[N];
int n, m;
bool st[N];

int dijkstra()
{
    // 初始化 d
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    // 处理 n 次，从而将 n 个顶点依次放到集合中
    for (int i = 0; i < n; i ++)
    {
        // 找到集合外 d 最小的顶点 u 
        int u = -1;
        for (int t = 1; t <= n; t ++)
            if (!st[t] && (u == -1 || d[t] < d[u]))
                u = t;

        // 将 u 放到集合中
        st[u] = true;

        // 用 u 更新其他顶点（只需更新邻接顶点）
        for (int v = 1; v <= n; v ++)
        {
            d[v] = min(d[v], d[u] + g[u][v]);
        }
    }
    if (d[n] == 0x3f3f3f3f) return -1;
    return d[n];
}

int main()
{
    cin >> n >> m;

    // 不连通则边权为无穷
    memset(g, 0x3f, sizeof g);

    // 只记录最小边权
    while (m --)
    {
        int x, y, w;
        cin >> x >> y >> w;
        g[x][y] = min(g[x][y], w);
    }

    cout << dijkstra() << endl;

    return 0;
}

堆优化算法

#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>

using namespace std;
using PII = pair<int, int>;

const int N = 1e6 + 10, INF = 0x3f3f3f3f;

int h[N], e[N], w[N], ne[N], idx;
int n, m;
int d[N];
bool st[N];
priority_queue<PII, vector<PII>, greater<PII>> heap;

void add(int x, int y, int wt)
{
    e[idx] = y, w[idx] = wt, ne[idx] = h[x], h[x] = idx ++;
}

int dijkstra()
{
    // 初始化 d
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    // 处理 n 次，从而将 n 个顶点依次放到集合中
    heap.push({0, 1});
    while (heap.size())
    {
        // 找到集合外 d 最小的顶点 u 
        int u = heap.top().second;
        heap.pop();
        if (st[u]) continue;

        // 将 u 放到集合中
        st[u] = true;

        // 用 u 更新其他顶点（只需更新邻接顶点）
        for (int i = h[u]; i != -1; i = ne[i])
        {
            int v = e[i];
            if (d[v] > d[u] + w[i])
            {
                d[v] = d[u] + w[i];
                heap.push({d[v], v});
            }
        }
    }

    if (d[n] = INF) return -1;
    return d[n];
}

int main()
{
    cin >> n >> m;
    // 初始化邻接表
    memset(h, -1, sizeof h);

    while (m --)
    {
        int x, y, wt;
        cin >> x >> y >> wt;
        add(x, y, wt);
    }

    cout << dijkstra() << endl;

    return 0;
}

Bellman-Ford

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510, M = 10010, INF = 0x3f3f3f3f;

struct {
    int a;
    int b;
    int w;
} edges[M];
int n, m, k;
int d[N], bak[N];

void bellman_ford()
{
    // 初始化 d
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    // 迭代 k 轮，则 d 至多更新 k 次
    while (k --)
    {
        memcpy(bak, d, sizeof d);
        for (int i = 0; i < m; i ++)
        {
            int a = edges[i].a, b = edges[i].b, w = edges[i].w;
            // 用上一轮边尾的d，更新本轮边头的d
            d[b] = min(d[b], bak[a] + w);
        }
    }
    // 负权边会略微扰动，使得两个不连通的顶点间的d值偏低
    if (d[n] > INF / 2) puts("impossible");
    else cout << d[n] << endl;
}

int main()
{
    cin >> n >> m >> k;

    for (int i = 0; i < m; i ++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }

    bellman_ford();

    return 0;
}

SPFA

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10, M = 1e5 + 10;

int h[N], e[M], w[M], ne[M], idx;
int n, m, k;
int q[N], hh, tt = -1;
bool st[N];
int d[N];

void add(int a, int b, int wt)
{
    e[idx] = b, w[idx] = wt, ne[idx] = h[a], h[a] = idx ++;
}

int spfa()
{
    // 初始化 d
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    // 将顶点 1 作为第一层顶点放入队列
    q[++ tt] = 1;
    st[1] = true;

    // 直到队列为 0，说明所有顶点的 d 无法继续更新
    while (tt >= hh)
    {
        // 取出上一层的顶点 u
        int u = q[hh ++];
        st[u] = false;

        // 访问 u 的所有邻接顶点 v
        for (int i = h[u]; i != -1; i = ne[i])
        {
            int v = e[i];

            // 如果 v 可以通过 u 进行更新
            if (d[v] > d[u] + w[i])  // 当所有顶点都不满足本条件时，队列大小将单调下降，算法趋于结束
            {
                // 更新 d[v]
                d[v] = d[u] + w[i];
                // 如果 v 不在队列中
                if (!st[v])
                {
                    // 将 v 放入队列
                    q[++ tt] = v;
                    st[v] = true;
                }
            }
        }
    }
    if (d[n] == 0x3f3f3f3f) cout << "impossible" << endl;
    else cout << d[n] << endl;
}

int main()
{
    memset(h, -1, sizeof h);

    cin >> n >> m;
    while (m --)
    {
        int x, y, wt;
        cin >> x >> y >> wt;
        add(x, y, wt);
    }

    spfa();

    return 0;
}