所谓二叉搜索树的“镜像”，即将所有结点的左右子树对换位置后所得到的树。
一个二叉搜索树经过变换之后，其对应的所有子树的左右节点都得到了互换。

镜像变换采用递归的思路，让根节点的左节点进行镜像变化，右节点进行镜像变化，之后再将左右节点进行镜像变化，最终返回root。

测试用例：

7
8 10 11 8 6 7 5

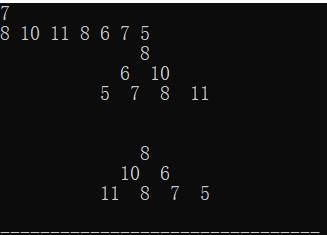
效果图：

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
struct TreeNode{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x),left(NULL),right(NULL) {}
};
int n,num;
TreeNode *root,*mirror_root;
TreeNode* insert(TreeNode* root,int val)    //插入节点构造二叉搜索树
{
    if(!root)
    {
        root = new TreeNode(val);
    }
    else if(root->val > val) root->left = insert(root->left,val);
    else root->right = insert(root->right,val);

    return root;
}
TreeNode* mirror(TreeNode* root)    //镜像变化函数
{
    if(!root) return NULL;
    root->left = mirror(root->left);    //左节点镜像变化
    root->right = mirror(root->right);  //右节点镜像变化
    auto temp = root->left;     //左右节点进行交换
    root->left = root->right;
    root->right = temp;
    return root;    //返回根节点的值
}
void bfs(TreeNode *root)
{
    queue<TreeNode*> q;
    q.push(root);

    int x=0;
    while(q.size())
    {
        int len=q.size();
        for(int i=0;i<len;i++)
        {
            int space=2*(n-x);
            auto t = q.front();
            q.pop();
            if(i==0)  for(int i=0;i<space;i++) cout<<" ";
            else  for(int i=0;i<2;i++) cout<<" ";
            cout<<t->val;
            if(t->left) q.push(t->left);
            if(t->right) q.push(t->right);
        }
        cout<<endl;
        x++;
    }
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>num;
        root = insert(root,num);
    }   

    bfs(root);

    cout<<endl;
    cout<<endl;

    mirror_root = mirror(root);
    bfs(mirror_root);

    return 0;
}