动态区间最大值

树状数组虽然优雅，但是不能处理较为复杂的区间问题。这时可以
用解决各种区间问题的终极武器：线段树
线段树能解决所有树状数组能解决的问题，还能支持更复杂的操作。
给定一个长度为 $𝑛(𝑛 \leqslant 10^5 )$ 的非负整数序列𝑎。
有很多次操作，每个操作可能是：

• $Q \ l \ r$ 询问 $max_{i=x}^y \{a_i\}$
• $M \ x \ y$ 将 $a_x$的值改为 $y$

线段树

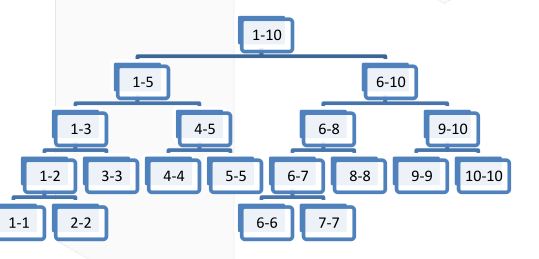
线段树的基本形态如下图。它的每个结点维护一段区间的信息，且
每个父结点维护的信息是两个子节点维护的区间的并。
具体地，如果一个线段树维护 $𝑛$ 个元素组成的序列，那么根节点维护
区间 $[1,𝑛]$，每个结点的左右儿子维护的区间分别是这个结点维护的
区间的一半。最后，叶子结点维护的区间长度为1，这棵线段树上一
共会有 $𝑛$ 个叶子结点。
线段树的深度为 $𝑂(\log𝑛)$

代码实现

由于线段树也是二叉树型结构，且形态较为紧凑（接近满二叉树），
也可以用数组模拟实现。根结点编号为 $1$，编号为 $pos$ 的结点的两个
子结点编号分别为 $pos * 2 $ 和 $pos*2+1$ 。方便起见，用宏定义代替。

#define lson ((pos) * 2)
#define rson ((pos) * 2 + 1)

需要注意的是，存储线段树的数组大小需要开到 $4*n$。本题中，我们
想维护区间最大值，就开一个数组 $tmax$，让 $tmax[pos]$ 表示编号为
$pos$ 的结点代表的区间中的最大值。

int tmax[4 * 100005];

单点修改时，从根节点出发，二分地查询 $x$ 所在的区间，递归到左儿
子或右儿子中，直至递归到叶子结点为止。时间复杂度 $𝑂(\log𝑛)$

void modify(int pos, int l, int r, int x, int y) {
    if (l == r) {
        tmax[pos] = y;
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) modify(lson, l, mid, x, y);
    else modify(rson, mid + 1, r, x, y);
    tmax[pos] = max(tmax[lson], tmax[rson]);
}

区间查询时，有可能会同时递归到左儿子或右儿子中，所以使用ret
将两个儿子中查询到的答案合并。递归到 $[l,r]$ 完全被 $[x,y]$ 包含时
为止，时间复杂度也是 $𝑂(\log𝑛)$ 的。

int query(int pos, int l, int r, int x, int y) {
    if (x <= l && r <= y) return tmax[pos];
    int mid = (l + r) >> 1;
    int ret = 0;
    if (x <= mid)
        ret = max(ret, query(lson, l, mid, x, y));
    if (y > mid)
        ret = max(ret, query(rson, mid + 1, r, x, y));
    return ret;
}

线段树在初始化的时候，当然可以把每个结点都初始化为 $0$，之后对
序列中元素分别执行一次修改。
也可以用下面的方式 $𝑂(𝑛)$ 地进行初始化。

void build(int pos, int l, int r) {
    if (l == r) {
        tmax[pos] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(lson, l, mid);
    build(rson, mid + 1, r);
    tmax[pos] = max(tmax[lson], tmax[rson]);
}

这些函数在使用的时候都以根节点作为入口。

• 初始化
  build(1, 1, n);
• $Q \ l \ r$ 询问 $max_{i=x}^y \{a_i\}$
  cout << query(1, 1, n, l, r) << endl;
• $M \ x \ y$ 将 $a_x$ 的值改为 $y$
  modify(1, 1, n, x, y);

动态区间和

线段树还可以维护各种花式操作：
给定一个长度为 $𝑛(𝑛 \leqslant 10^5 )$ 的非负整数序列 $𝑎$。

• $M \ l \ r \ k \ $ 将 $a_{[l, r]}$每个数加上 $k$
• $Q \ x \ y \ $ 询问 $\sum_{i=x}^y a_i$

区间修改

线段树维护区间和与维护区间最大值大同小异，只需要把之前代码
中的 “max” 改成 “+” 即可。
但是，这道题中要维护区间修改操作。每进行一次区间修改，线段
树上都可能有 $𝑂(𝑛)$ 个结点处保存的值要发生改变。如何解决这一问
题呢？

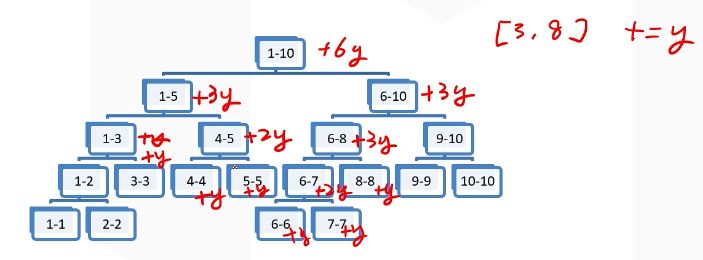
我们可以采用延迟修改法。对一个结点进行修改之后，不急着去递
归地修改它的子孙，而是在这个结点上打一个“懒标记”。以后需
要访问它的子孙的信息时，再去将标记下传。
这样，每个修改和查询操作的时间复杂度还是 $𝑂(\log𝑛)$。

代码实现

void modify(int pos, int l, int r, int x, int y, int k) {
    if (x <= l && r <= y) {
    tsum[pos] += k * (r - l + 1);
    lazy[pos] += k;
    return;
    }
    pushdown(pos, l, r);
    int mid = (l + r) >> 1;
    if (x <= mid) modify(lson, l, mid, x, y, k);
    if (y > mid) modify(rson, mid + 1, r, x, y, k);
    tsum[pos] = tsum[lson] + tsum[rson];
}

void pushdown(int pos, int l, int r) {
    int mid = (l + r) >> 1;
    tsum[lson] += lazy[pos] * (mid - l + 1);
    lazy[lson] += lazy[pos];
    tsum[rson] += lazy[pos] * (r - mid);
    lazy[rson] += lazy[pos];
    lazy[pos] = 0;
}

int query(int pos, int l, int r, int x, int y) {
    if (x <= l && r <= y) return tsum[pos];
    pushdown(pos, l, r);
    int mid = (l + r) >> 1;
    int ret = 0;
    if (x <= mid) ret += query(lson, l, mid, x, y);
    if (y > mid) ret += query(rson, mid + 1, r, x, y);
    return ret;
}

组合型区间操作

还可以让操作更花哨一点：
给定一个长度为 $𝑛(𝑛 \leqslant 10^5)$ 的非负整数序列𝑎。
有很多次操作，每个操作可能是：

• $A \ l \ r \ k \ $ 将 $𝑎_{[𝑙,𝑟]}$ 每个值加上 $k$
• $B \ l \ r \ k \ $ 将 $𝑎_{[𝑙,𝑟]}$ 每个值乘上𝑙
• $P \ x \ y \ $ 询问 $max_{i=x}^y a_i$
• $Q \ x \ y \ $ 询问 $\sum_{i=x}^y a_i$

现在有两个区间修改，那么只需要对节点设加法和乘法两个标记。
注意区间乘法的操作以及乘法标记的下传都会对加法标记产生影响。
这道题还有两个询问，分别维护即可。
总而言之，线段树可以维护许多复杂的区间问题。

例1： 【模板】线段树 1

Solution:

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
#define MAXN 100005

ll n, m;
ll a[MAXN];
ll sum[MAXN * 4];
ll tag[MAXN * 4];

inline ll lc(ll p) { return p << 1; }

inline ll rc(ll p) { return p << 1 | 1; }

// 根据孩子信息把当前信息还原出来 
void pushUp(ll p) {
    sum[p] = sum[lc(p)] + sum[rc(p)];
}

void buildTree(ll p, ll l, ll r) {
    if (l == r) {
        sum[p] = a[l];
        return;
    }
    ll mid = (l + r) >> 1;
    buildTree(lc(p), l, mid);
    buildTree(rc(p), mid + 1, r);
    pushUp(p);
}

void moveTag(ll p, ll l, ll r, ll t) {
    sum[p] += t * (r - l + 1);
    tag[p] += t;
}

void pushDown(ll p, ll l, ll r) {
    ll mid = (l + r) >> 1;
    moveTag(lc(p), l, mid, tag[p]); // 把我的tag传给孩子 
    moveTag(rc(p), mid + 1, r, tag[p]);
    tag[p] = 0;
}

void update(ll p, ll l, ll r, ll ql, ll qr, ll d) {
    if (ql <= l && r <= qr) { // 表示p是终止节点 
        sum[p] += d * (r - l + 1);
        tag[p] += d;
        return;
    }
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    if (ql <= mid) {
        update(lc(p), l, mid, ql, qr, d);
    } 
    if (mid < qr) {
        update(rc(p), mid + 1, r, ql, qr, d);
    }
    pushUp(p);
}

ll query(ll p, ll l, ll r, ll ql, ll qr) {
    if (ql <= l && r <= qr) return sum[p];
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    ll res = 0;
    if (ql <= mid) {
        res += query(lc(p), l, mid, ql, qr);
    }
    if (mid < qr) {
        res += query(rc(p), mid + 1, r, ql, qr);
    }
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    buildTree(1, 1, n);
    while (m--) {
        int op; cin >> op;
        if (op == 1) {
            int x, y, k;
            cin >> x >> y >> k;
            update(1, 1, n, x, y, k);
        }
        else {
            int x, y;
            cin >> x >> y;
            cout << query(1, 1, n, x, y) << '\n';
        }
    }
    return 0;
}

例2： 【模板】线段树 2

Solution:

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

const int N = 100005;

ll m, n, mod;
ll a[N];
ll sum[N * 3];
ll addTag[N * 3];
ll mulTag[N * 3];

inline ll lc(ll x) { return x << 1; }

inline ll rc(ll x) { return x << 1 | 1; }

void pushUp(ll p) {
    sum[p] = (sum[lc(p)] + sum[rc(p)]) % mod;
}

void build(ll p, ll l, ll r) {
    addTag[p] = 0;
    mulTag[p] = 1;
    if (l == r) {
        sum[p] = a[l] % mod;
        return;
    }
    ll mid = (l + r) >> 1;
    build(lc(p), l, mid);
    build(rc(p), mid + 1, r);
    pushUp(p);
}

void moveTag(ll p, ll l, ll r, ll mt, ll at) {
    sum[p] = (sum[p] * mt + at * (r - l + 1)) % mod;
    addTag[p] = (addTag[p] * mt + at) % mod;
    mulTag[p] = (mulTag[p] * mt) % mod;
}

void pushDown(ll p, ll l, ll r) {
    ll mid = (l + r) >> 1;
    moveTag(lc(p), l, mid, mulTag[p], addTag[p]);
    moveTag(rc(p), mid + 1, r, mulTag[p], addTag[p]);
    mulTag[p] = 1;
    addTag[p] = 0;
}

void addUpdate(ll p, ll l, ll r, ll ql, ll qr, ll k) {
    if (ql <= l && r <= qr) {
        sum[p] = (sum[p] + k * (r - l + 1)) % mod;
        addTag[p] = (addTag[p] + k) % mod;
        return;
    }
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    if (ql <= mid) {
        addUpdate(lc(p), l, mid, ql, qr, k);
    }
    if (mid < qr) {
        addUpdate(rc(p), mid + 1, r, ql, qr, k);
    }
    pushUp(p);
}

void mulUpdate(ll p, ll l, ll r, ll ql, ll qr, ll k) {
    if (ql <= l && r <= qr) {
        sum[p] = (sum[p] * k) % mod;
        mulTag[p] = (mulTag[p] * k) % mod;
        addTag[p] = (addTag[p] * k) % mod;
        return;
    }
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    if (ql <= mid) {
        mulUpdate(lc(p), l, mid, ql, qr, k);
    }
    if (mid < qr) {
        mulUpdate(rc(p), mid + 1, r, ql, qr, k);
    }
    pushUp(p);
}

ll query(ll p, ll l, ll r, ll ql, ll qr) {
    if (ql <= l && r <= qr) return sum[p] % mod;
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    ll ans = 0;
    if (ql <= mid) {
        ans += query(lc(p), l, mid, ql, qr);
    }
    if (mid < qr) {
        ans += query(rc(p), mid + 1, r, ql, qr);
    }
    return ans % mod;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m >> mod;

    for (int i = 1; i <= n; ++i) cin >> a[i];

    build(1, 1, n);

    for (int i = 0; i < m; ++i) {
        ll t, x, y, z;
        cin >> t;
        if (t == 1) {
            cin >> x >> y >> z;
            mulUpdate(1, 1, n, x, y, z);
        }
        else if (t == 2) {
            cin >> x >> y >> z;
            addUpdate(1, 1, n, x, y, z);
        }
        else {
            cin >> x >> y;
            cout << query(1, 1, n, x, y) << '\n';
        }
    }

    return 0;
}

动态开点线段树

• 如果线段树需要维护的区间很大很大，但是实际用到的节点很少很少
• 在线操作不能离散化
• 不要开那么多的节点，用到的时候再向内存要，总内存消耗 $O(n\log V)$
• 建立了一颗残疾的线段树，缺少很多枝叶

例题：有便便的厕所

数据范围很大，决定动态开点
有范围删除操作，记录一个 del 的 $tag$，表示是否当前节点内所有元素都被删除掉

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

const int INF = 1000000005;
const int MX = 100005;

struct Node {
    int cnt, del, lc, rc; // cnt ｱ桄ｾﾇ菲ﾏｵ羞ﾄｸ｣ｬdel ｱ桄ｾﾇ萍ﾇｷｻﾉｾﾁﾋ 
} tree[MX * 50];
int q, nn = 1; // nn ｱ桄ｾﾏﾂﾒｻｸｪﾓﾃｵﾄｵ・

void pushUp(int p) {
    tree[p].cnt = tree[tree[p].lc].cnt + tree[tree[p].rc].cnt;
} 

void moveTag(int p) {
    tree[p].del = 1;
    tree[p].cnt = 0;
}

void pushDown(int p) {
    if (tree[p].del == 1) {
        tree[p].del = 0;
        moveTag(tree[p].lc);
        moveTag(tree[p].rc);
    }
}

void insert(int p, int l, int r, int q) {
    if (l == r) {
        tree[p].del = 0;
        tree[p].cnt++;
        return;
    }
    pushDown(p);
    int mid = (l+r) / 2;
    if (q <= mid) {
        if (tree[p].lc == 0) tree[p].lc = ++nn;
        insert(tree[p].lc, l, mid, q);
    }
    else {
        if (tree[p].rc == 0) tree[p].rc = ++nn;
        insert(tree[p].rc, mid+1, r, q);
    }
    pushUp(p);
}

void remove(int p, int l, int r, int ql, int qr) {
    if (p == 0 or tree[p].del == 1 or tree[p].cnt == 0) return;
    if (ql <= l and r <= qr) {
        tree[p].del = 1;
        tree[p].cnt = 0;
    }
    pushDown(p);
    int mid = (l+r) / 2;
    if (ql <= mid) {
        remove(tree[p].lc, l, mid, ql, qr);
    }
    if (mid < qr) {
        remove(tree[p].rc, mid+1, r, ql, qr);
    }
    pushUp(p);
}

int querySum(int p, int l, int r, int ql, int qr) {
    if (p == 0 or tree[p].del == 1 or tree[p].cnt == 0) {
        return 0;
    }
    if (ql <= l and r <= qr) {
        return tree[p].cnt;
    }
    pushDown(p);
    int res = 0;
    int mid = (l+r) / 2;
    if (ql <= mid) {
        res += querySum(tree[p].lc, l, mid, ql, qr);
    }
    if (mid < qr) {
        res += querySum(tree[p].rc, mid+1, r, ql, qr);
    }
    return res;
}

int queryK(int p, int l, int r, int ql, int qr, int k) {
    if (p == 0 or tree[p].cnt == 0 or tree[p].del == 1) return -1;
    if (l == r) {
        if (tree[p].cnt >= k) return l;
        else return -1;
    }
    pushDown(p);
    int mid = (l+r) / 2;
    int cnt = 0;
    int lc = tree[p].lc, rc = tree[p].rc;
    if (mid < qr) {
        cnt = querySum(rc, mid+1, r, ql, qr);
        if (cnt >= k) {
            return queryK(rc, mid+1, r, ql, qr, k);
        }
    }
    if (ql <= mid) {
        return queryK(lc, l, mid, ql, qr, k-cnt);
    }
    return -1;
}

int main() {
    cin >> q;

    rep(i, q) {
        int type, x, l, r, k;
        cin >> type;
        if (type == 1) {
            cin >> x;
            insert(1, 1, INF, x);
        } 
        else if (type == 2) {
            cin >> l >> r;
            remove(1, 1, INF, l, r);
        }
        else {
            cin >> l >> r >> k;
            cout << queryK(1, 1, INF, l, r, k) << '\n';
        }
    }

    return 0;
}

一些练习题

1. 小白逛公园
2. I Hate It
3. gcd区间
4. 最大数
5. Range Xor Query
6. 你能回答这些问题吗
7. 区间最大公约数