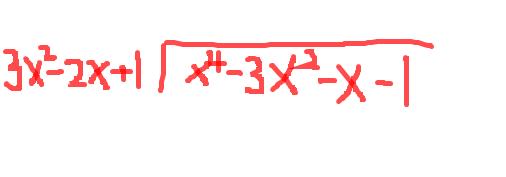首先输入被除数的项数n1，之后输入被除数的指数和系数，
之后再输入除数的项数n2，之后再输入除数的指数和系数，
求多项式的商和余数，要求输出时系数要保留1位小数。

输入样例

4 4 1 2 -3 1 -1 0 -1
3 2 3 1 -2 0 1

输出样例

3 2 0.3 1 0.2 0 -1.0
1 1 -3.1

除法图例：

分析

多项式的除法，需要将被除数的系数储存起来，同时将除数的指数与系数同时储存起来，保持下标一致。
在除的过程中for循环的范围为a的最高次幂（amax）到b的最高次幂（b1[0]），用c来表示商的系数，a数组即被除数数组表示最终的余数。
除法结束后要根据每一项系数的绝对值是否大于0.05（因为保留1位小数）来判断一共输出几项。
如果cnt为0，说明没有系数可以输出，即零系数，要输出“ 0 0.0”。

C++ 代码

#include<bits/stdc++.h>
using namespace std;
int n1,n2,zhi,amax=-1;
const int N =1e5+10;
double xi,a[N],b2[N],c[N];
int b1[N];
int main()
{
    cin>>n1;
    for(int i=0;i<n1;i++)
    {
        cin>>zhi>>xi;
        a[zhi]=xi;
        if(zhi>amax) amax=zhi;      //保存a的最高次幂
    }
    //for(int i=0;i<n;i++) cout<<a[i]<<endl;
    cin>>n2;
    for(int i=0;i<n2;i++)
    {
        cin>>b1[i]>>b2[i];
    }
    //for(int i=0;i<n;i++) cout<<b1[i]<<" "<<b2[i]<<endl;
    for(int i=amax;i>=b1[0];i--)
    {
        int czhi=i-b1[0];
        c[czhi]=a[i]/b2[0];     //c来表示商的系数
        for(int j=0;j<n2;j++)   //用刚刚得到的商的系数来修改a数组
        {
            a[czhi+b1[j]]-=c[czhi]*b2[j];   //减去系数*除数的系数b2[j]及每次余数的系数
        }
    }
    int cnt1=0,cnt2=0;
    for(int i=amax;i>=0;i--)    //由于保留1位小数，绝对值大于等于0.05的可以当做一项输出，故cnt++
    {
        if(fabs(c[i])>=0.05) cnt1++;
        if(fabs(a[i])>=0.05) cnt2++;
    }
    cout<<cnt1;
    for(int i=amax;i>=0;i--)    //输出商
    {
        if(fabs(c[i])>=0.05)
        {
            printf(" %d %.1lf",i,c[i]);
        }
    }
    if(cnt1==0) cout<<" 0 0.0";
    cout<<endl;
    cout<<cnt2;
    for(int i=amax;i>=0;i--)    //输出余数
    {
        if(fabs(a[i])>=0.05)
        {
            printf(" %d %.1lf",i,a[i]);
        }
    }
    if(cnt2==0) cout<<" 0 0.0";
    return 0;
}