$平面图的定义$

设无向图 $G$，若能将 $G$ 画在一个平面上，使得任何两条边仅在顶点处相交，则称 $G$ 是具有平面性质的图，简称平面图，否则称 $G$ 是非平面图。

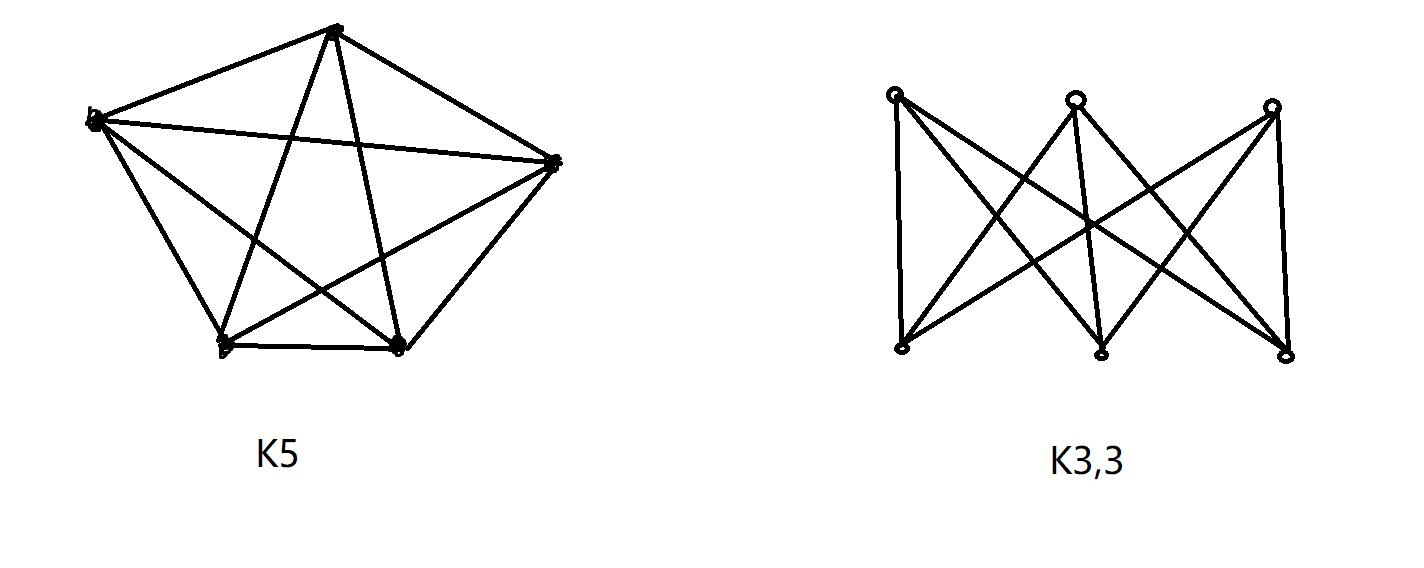
$K_{3,3}$ 和 $K_5$ 都不是平面图。

$平面图的概念$

若现有一个平面图 $G$，$G$ 上的边将其所在的平面划分成一个个面，有限的区域为有限面，无限的区域为无限面，与无限面有交的边称为桥，一个面边界上边的数量为它的次数。

$欧拉公式$

定理

设 $G$ 为一个联通平面图，$n$ 为其点数，$m$ 为其边数，$f$ 为其面数（包含无限面），则有 $n-m+f=2$。

证明

进行 $m$ 此如下操作：

• 若存在一个点的度数为 $1$，则删去这个点和连接它的这条边，$n$ 和 $m$ 各减一，$n-m+f$ 的值不变。

• 否则一定存在一个环，删去环上的一条边，则 $m$ 和 $f$ 各减一，$n-m+f$ 的值不变。

由于每次 $m$ 的值都会减一，所以最终 $m = 0, n = 1, f = 1, n - m + f = 2$ ，证毕。

推论1

有联通平面图 $G$，$n\ge 3$，每个面的次数至少为 $p(p\ge 3)$，则 $m\leq \frac{p(n-2)}{p-2}$。

证明

由于图联通，则有欧拉公式 $n-m+f=2$，由于每个面次数至少为 $p$ 所以总次数至少为 $p\cdot f$，由于总次数一定是 $2m$，所以有 $2m\ge p\cdot f$，带入欧拉公式得

$$2m\ge p(2-n+m)$$

$$m(2-p)\ge p(2-n)$$

$$m\leq \frac{p(2-n)}{2-p}$$

$$m\leq \frac{p(n-2)}{p-2}$$

推论2

根据推论1，有一个联通平面图 $G$，满足 $n\ge 3$，将 $p=3$ 带入，得到 $m\leq 3n-6$

$平面图的判断$

同胚操作

在无向图 $G$ 中加入或删除一个度数为 $2$ 的点，图的平面性不变。

库拉图斯基定理

图 $G$ 是平面图当且仅当 $G$ 不含与 $K_5$ 或 $K_{3,3}$ 同胚的子图。

图 $G$ 是平面图当且仅当 $G$ 中没有可以收缩到 $K_5$ 或 $K_{3,3}$ 的子图。

$对偶图$

现有一个平面图 $G$，将 $G$ 的每一个面视作一个点，每一条分割两个面的边，视作这两个面之间的边，于是构造出了图 $G$ 的对偶图。