宣传一波 更好的阅读体验 👉 个人blog

数字签名原理

一个完整的数字签名方案由三部分组成:密钥生成算法、签名算法和验证算法。密钥生成算法是根据系统参数为签名者生成公钥和私钥;签名算法是产生数字签名的某种算法,而验证算法是检验一个数字签名是否有效(即是否由指定实体生成)的某种算法。如无特殊说明,下文继续用 A 代表签名者,B 代表验证者。

下面给出数字签名的形式化定义:

(1)密钥生成算法

系统初始化产生签名方案的基本参数(M,S,K,Sign,Ver),其中 M 为消息空间,S 为签名空间，K 为密钥空间，包含私钥和公钥,Sign 为签名算法集合,Ver 为签名验证算法集合。用户 A 执行密钥生成算法生成自己的公私密钥$(k_1,k_2)$。

(2)签名算法

对任意的消息 $m \in M$,有$s=sign_{k_2}(m)$,且$s \in S$,那么 s 为消息的签名,将签名消息组(m,s)发送给签名验证者。

(3)验证算法

对于上述的$k_1 \in K$,有相应的签名验证算法:$ver_{k_1}:M \times S \rightarrow \lbrace True,False \rbrace,ver_{k_1} \in Ver$,且

$$ver_{k1}(m, s) = \begin{cases} True & 当 s = sign_{k_2} \newline False & 当s \neq sign_{k_2} \end{cases}$$

签名验证者收到(m,s)后,计算 $ver_{k_1}(m,s)$,若 $ver_{k_1}(m,s)=True$,则签名有效;否则签名无效。

对于每一个$k \in K$,签名函数$sign*{k_2}$,和签名验证函数 $ver*{k*1}$, 是容易计算的。而验证函数 $ver*{k*1}$是公开的,同时还要求对任意的消息 m,在未知$k_2$条件下从集合 S 中选取 s 使得 $ver*{k_1}(m,s)=True$ 是非常困难的,也就是说,攻击者对消息 m 产生有效的签名 s 是不可能的。

根据定义,在进行私钥签名前,先进行消息关键信息提取。

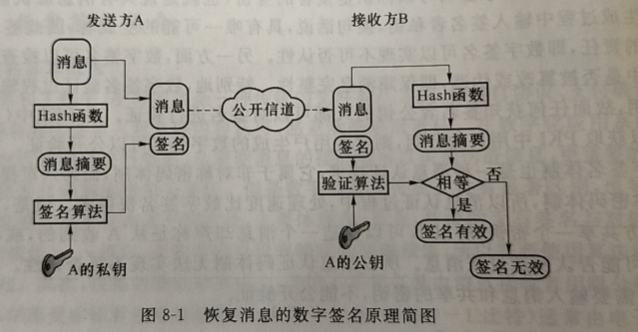
如图 8-1 所示,发送方 A 将消息用 Hash 算法产生一个消息摘要(Message Digest),这个消息摘要有两个重要特性:抗碰撞性和摘要长度固定,使得任何消息产生的签名值长度是一样的。发送方 A 产生消息摘要后,用自己的私钥对摘要进行加密,这个加密后的消息摘要就是数字签名，随后发送方 A 将消息与签名发给接收方 B。B 接收到消息及其签名后,用发送方 A 的公钥解密这个签名,获得由发送方 A 生成的消息摘要,接着用发送方 A 所用 Hash 算法重新生成所获得消息的摘要,然后比对这两个摘要。如果相同,说明这个签名是发送方 A 针对这个消息的有效签名;如果不相同,则签名无效。

依据上述数字签名的基本原理,人们设计出了众多不同种类的数字签名方案,下面将介绍常用数字签名的实现方案。

ElGamal签名体制

T. EIGamal于1985年提出了一个基于有限域离散对数问题的数字签名方案,美国NIST确立的数字签名标准(Digital Signature Standard,DSS)即是在它基础上修订的。EIGamal数字签名方案是一种非确定性的签名方案,即对给定的一个消息,由于选择的随机数不同而产生不同的数字签名,并且验证算法均会判断为有效。下面简要介绍其方案的实现过程。

1. 密钥生成算法

选择一个满足安全性要求的大素数 p,然后选择一个生成元 $g \in Z^*_p$;和随机数$x \in _RZ^*_p$，,计算$y \equiv g^x(mod\ p)$。则签名者A的公钥为(p，g，y),私钥为x。

1. 签名算法
   设待签消息为 m，签名者选择随机数$k \in _RZ^*_p$;,计算:
   $$\begin{aligned} &r \equiv g^k(mod \ p) \newline &s \equiv [h(m)-xr]k^{-1}(mod \ (p-1)) \end{aligned}$$
   则对消息 m的数字签名为(r，s),其中h为安全的 Hash 函数

2. 验证算法

签名接收者 B收到消息 m 和签名(r，s)后,首先计算 h(m),然后验证下列等式是否成立
$$y^rr^s \equiv g^{h(m)}(mod \ p)$$

如等式成立,则签名有效;否则,签名无效。

1. 正确性

如果所有算法按步骤执行,则接收者输出签名有效,因为
$$r \equiv g^k(mod \ p), s \equiv [h(m) - xr]k ^{-1}(mod \ (p - 1))$$
所以
$$\begin{aligned} & ks \equiv h(m) - xr(mod \ (p - 1)) \newline & g^{ks} \equiv g^{h(m) - xr}(mod \ p) \newline & g^{ks}g^{xr} \equiv g^{h(m)}(mod \ p) \newline & y^rr^s \equiv g^{h(m)}(mod \ p) \end{aligned}$$

案例

1. 密钥生成算法

假设A选取素数 p=19,$Z^*_p$的生成元g=2。选取私钥x=15,计算:
$$y=g^x \ mod \ p=2^{15} \ mod \ 19 = 12$$
则A的公钥是(p=19，g=2，y=12)。

1. 签名算法
   设消息m的Hash值h(m)=16,则A选取随机数k = 11，计算:
   $$\begin{aligned} &r=g^k \ mod \ p \equiv 2^{11} \ mod \ 19=15\newline &k^{-1} \ mod \ (p-1) = 5 \end{aligned}$$
   最后计算签名
   $$s=[h(m)-xr]k^{-1} \ mod \ (p-1)=5(16-15 \times 15) \ mod \ 18=17$$
   A对m的签名为(15，17)。

2. 验证算法

接收者 B得到签名(15,17)后计算:
$$\begin{aligned} y^rr^s \ mod \ p=12^{15}15^{17} \ mod \ 19=5\newline g^{h(m)} \ mod \ p \equiv 216 \ mod \ 19=5 \end{aligned}$$
验证等式
$$y^rr^s \equiv g^{h(m)}(mod \ p)$$
成立，因此B接受签名。

注意,本例旨在说明该方案的实现过程,为计算方便所选参数均较为简单。按目前计算能力,通常使用 1024 比特或更大的模数。

C++代码

在写代码的时候我并没有学习优先于离散对数问题（懒），因此，关于生成元g的知识我并不清楚，我是直接copy的生成元函数，但是我会适当的加上我的理解的注释

#include <stdio.h>
#include <time.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>

using namespace std;

typedef long long LL;

int mod(int a,int b){
    int ans;
    while(a<0){
        a=a+b;
    }
    ans=a%b;
    return ans;
}

// 指数运算
// 输入a和b
// 输出a的b次方
int power(int a, int b)
{
    int temp = a;
    for(int i=1 ; i<b ; i++)
    {
        temp = temp * a;
    }
    return temp;
}

// 判断一个数是否为素数
// 输入一个数a
// 返回：如果a是素数，返回true ； 否则返回false
bool Prime(int a)
{
    for(int i=2 ; i<= (a/2) ; i++)
    {
        if((a % i) == 0)
        {
            return false;
        }
    }
    return true;
}

// 辗转相除法
// 输入 a 和 b
// 返回 a和b 的最大公约数
int gcd(int a , int b)
{
    while(b!=0)
    {
        int temp = a % b;
        a = b;
        b = temp;
    }
    return a;
}

// 欧拉函数
// 输入a
// 返回a的欧拉函数值
int euler(int a)
{
    int b = 0;
    for(int i=1 ; i<a ; i++)
    {
        if(gcd(a,i) == 1)
        {
            b += 1;
        }
    }
    return b;
}

// 求阶函数
// 作用是找到最小的正整数 p（p < n），p % a == 0
int order(int a, int n, int b)
{
    int  p = 1;

    while( p<=n && power(b,p%a) != 1)
    {
        p += 1;
    }

    p = p - 1;

    if (p <= n)
    {
        return p;
    }
    else
    {
        return -1;
    }
}

// 公钥p的生成函数
int Generate_p()
{
    srand((unsigned int)time(NULL));
    int p = (rand() % (10000 - 1000 + 1) + 1000);

    for(; p<10000 ; p++)
    {
        if (Prime(p)==true)
        {
            return p;
        }
    }
}

// 公钥g的生成函数
int Generate_g(int p)
{

    int n = euler(p);

    for(int a = 2; a<p ; a++)
    {

        if(order(p,n,a) == n)
        {
            return a;
        }
    }
}

// 密钥x的生成函数
int Generate_x(int p)
{
    srand((unsigned int)time(NULL));
    int d = rand() % ( p-2-2+1) + 2;

    return d;
}

// 随机数k的生成函数
int Generate_k(int p)
{
    srand((unsigned int)time(NULL));
    int X = rand() % p;

    return X;
}
// 快速模幂运算
// 形式为 (a^b) mod c
// 输入 a 、b 和 c  因为要求a^b ， 因此是长整数
// 返回 (a^b) mod c 计算结果
int qmi(LL a, LL b, int c)
{
    int res = 1;
    while(b > 0)
    {
        if(b & 1)
        {
            res = (res * a) % c;
        }

        b = b >> 1;
        a = (a * a) % c;
    }
    return res;
}


// 求解乘法逆元
// 输入num 和 mod。 求num 在 mod 下的乘法逆元
// 返回num 在 mod 下的乘法逆元
int inverse(int num,int mod)
{
    int a = num;
    int b = mod;
    int x = 0, y = 1, x0 = 1, y0 = 0;
    int qt, temp;

    while(b != 0)
    {
        qt = a / b;
        temp = a % b;

        a = b;
        b = temp;

        temp = x; x = x0 - qt * x; x0 = temp;
        temp = y; y = y0 - qt * y; y0 = temp;
    }

    if(x0 < 0)
    {
        x0 += mod;
    }

    return x0;
}




int main()
{
    cout << "ElGamal签名验证开始O(∩_∩)O" << endl;
    cout << "=================================================" <<endl;
    //ElGamal密钥生成
    cout <<"1.ElGamal密钥生成如下:" << endl << endl;
    int p = Generate_p();
    int g = Generate_g(p);
    int x = Generate_x(p);
    int y = qmi(g, x, p);
    cout << "随机数x为:" << x << endl;
    cout << "签名者A的公钥{p,g,y}为:{" << p << "," << g << "," << y << "}" << endl;
    cout << "=================================================" <<endl;

    cout <<"2.ElGamal签名开始:" << endl << endl;
    int k = 1; // 随机数
    int in_k = inverse(k, p - 1); // k在mod(p-1)下的逆元
    int hm = Generate_p(); // 随机一个明文
    int r = qmi(g, k, p);
    int s = mod((hm - x * r) * in_k , (p - 1));
    cout << "明文hash后的值为" << hm << endl;
    cout << "随机数k和逆元in_k为:" << k << ","<< in_k <<endl;
    cout << "A对消息的数字签名{r,s}为:{" << r << "," << s << "}" << endl;
    cout << "=================================================" <<endl;

    cout <<"3.ElGamal验证开始:" << endl << endl;
    //防止计算过程中量太大，将算式拆分多次mod
    //y = 12,r = 15, p = 19, s = 17;
    //hm = 16,g = 2;
    int yr = qmi(y, r, p);
    int rs = qmi(r, s, p);
    int yrrs = mod(yr *rs, p);

    int ghm = qmi(g, hm, p);
    cout << "通过y,r,p计算yrrs mod p的值为:" << yrrs <<endl;
    cout << "通过g,hm,p计算ghm mod p的值为:" <<ghm << endl;
    if(yrrs == ghm) cout << "两值一致，数字签名验证有效!";
    else cout << "两值不一致，数字签名验证无效!";

    return 0;
}

结果

ElGamal签名验证开始O(∩_∩)O
=================================================
1.ElGamal密钥生成如下:

随机数x为:3998
签名者A的公钥{p,g,y}为:{4001,2,3001}
=================================================
2.ElGamal签名开始:

明文hash后的值为4001
随机数k和逆元in_k为:1,1
A对消息的数字签名{r,s}为:{2,5}
=================================================
3.ElGamal验证开始:

通过y,r,p计算yrrs mod p的值为:2
通过g,hm,p计算ghm mod p的值为:2
两值一致，数字签名验证有效!

安全性

使用 EIGamal数字签名方案应注意以下安全问题:

1. 随机数k值的选取和保管

首先,k 值不能泄露。如果k值泄露,则容易计算$x=[ h(m)-sk]r^{-1} \ mod \ (p-1$),签名者
的私钥泄露。

其次，随机数k不能重复使用。假设 k 用来对两个不同的消息签名，则r相同,即$(r,s_1)是m_1$的签名,$(r,s_2)是m_2$的签名。因为
$$\begin{aligned} s_1 \equiv [h(m_1)-xr]k^{-1} \ (mod \ (p-1))\newline s_2 \equiv [ h(m_2)-xr]k^{-1} \ (mod \ (p-1)) \end{aligned}$$
那么有
$$(s_1-s_2)k \equiv [ h(m_1)-h(m_2)](mod \ (p-1))。$$
又因为消息$m_1和m_2$不同,则$s_1-s_2 \neq 0 \ mod \ (p-1)$的概率很大,则
$$k \equiv [ h(m_1)-h(m_2)](s_1-s_2)^{-1}(mod \ (p-1))$$

进而容易计算签名者的私钥x。
最后，签名者多次签名时所选取多个 k 之间无关联。例如，三个不同的签名所选取的随机数为$k_1、k_2、k_3$,满足条件$k_3= k_1+k_2$，显然有$r_3= r_1 r_2$,则:

由$s \equiv [h(m)-xr]k^{-1} \ (mod \ (p-1))$可得$h(m) \equiv (ks+xr)(mod \ (p-1))$

因此有:
$$\begin{aligned} h(m_1)=(xr_1+ k_1s_1)(mod \ (p-1)) \newline h(m_2)=(xr_2+ k_2s_2)(mod \ (p-1)) \newline h(m_3)=(xr_3+ k_3s_3)(mod \ (p-1))\ \end{aligned}$$

对以上三式分别乘以$s_2s_3,s_1s_3,s_1s_2$ 得:
$$\begin{align} h(m_1)s_2s_3=(xr_1s_2s_3+ k_1s_1s_2s_3)(mod \ (p-1)) \newline h(m_2)s_1s_3=(xr_2s_1s_3+ k_2s_1s_2s_3)(mod \ (p-1)) \newline h(m_3)s_1s_2=(xr_3s_1s_2+ k_3s_1s_2s_3)(mod \ (p-1)) \end{align}$$
计算式(1)+式(2)-式(3)得
$$x\equiv[h(m_1)s_2s_3+ h(m_2)s_1s_3- h(m_3)s_1s_2](r_1s_2s_3+r_2s_1s_3-r_3s_1s_2)^{-1}(mod \ (p-1))$$
就可以从中推出签名者的私钥x。
由此可见，随机数 k的选取和保管对私钥x的保密性起着重要的作用。此外，随机数的使用也保证了签名方案的不可重用性，这是因为在不同时刻选取的随机数不同，即使对同一消息进行签名，也会产生不同的结果,因而避免了 RSA 签名出现的签名重用问题。

1. Hash 函数的应用
   如果未使用 Hash 函数则签名方案容易受到攻击。例如攻击者可以选取任一整数对(u,v),满足gcd(u,p-1)=1。计算$r=g^uy^v \ (mod \ p)，s \equiv -rv^{-1}(mod \ (p-1))和m \equiv su(mod \ p)$,则消息 m及其签名(r,s)可以被验证者接受,即攻击者成功进行存在性伪造。这是因为
   $$y^rr^s \equiv y^r(g^ug^v)^s \equiv y^{r + sv}·g^{us} \equiv y^{r+(-rv^{-1})}·g^{su} \equiv g^m(mod \ p)$$
   又因为$g^m \equiv g^{su}(mod \ p)$也就是说,签名(r,s)使等式$y^rr^s \equiv g^m(mod \ p)$成立。可见,使用 Hash函数能够有效地提高 EIGamal数字签名方案的安全性。