排序算法 总结

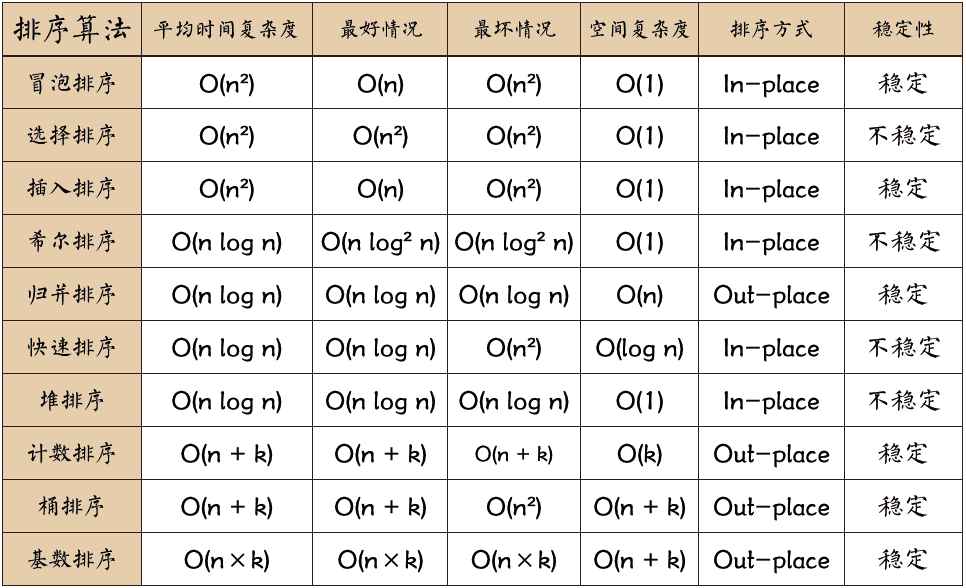
• in-place 占用常数内存，不占用额外内存
• out-place 占用额外内存，内存与n相关

排序算法可视化网页

1冒泡排序

void bubble_sort(int* a, int n)
{
    for (int i = n-1; i >= 1; i -- )
    {
        bool flag = true;
        for (int j = 1; j <= i; j ++ )
            if (a[j-1] > a[j])
            {
                swap(a[j-1], a[j]);
                flag = false;
            }
        if (flag) return;
    }
}

2选择排序

void select_sort(int *a, int n)
{
    for (int i = 0; i < n; i ++ )
    {
        int k = i;
        for (int j = i+1; j < n; j ++ )
        {
            if (a[j] < a[k])
                k = j;
        }
        swap(a[i], a[k]);
    }

}

3插入排序

void insert_sort(int *a, int n)
{
    for (int i = 1; i < n; i ++ )
    {
        int x = a[i];
        int j = i-1;

        while (j >= 0 && x < a[j])
        {
            a[j+1] = a[j];
            j -- ;
        }
        a[j+1] = x;
    }
}

4希尔排序

void shell_sort(int *a, int n)
{
    for (int gap = n >> 1; gap; gap >>= 1)
    {
        for (int i = gap; i < n; i ++ )
        {
            int x = a[i];
            int j;
            for (j = i; j >= gap && a[j-gap] > x; j -= gap)
                a[j] = a[j-gap];
            a[j] = x;
        }
    }
}

AcWing 787.归并排序
AcWing 788.逆序对数量

5归并排序 - 是二分的两个有序序列归并为一个有序序列

• 思想：分治，二叉树划分，递归
• 注意：需要开一个tmp数组存放左子树和右子树中小的一个，一直保证从两个有序子树中取值

void merge_sort(int *a, int l,int r)
{
    if(l >= r) return ;

    int mid = l + r >> 1;

    merge_sort(a, l, mid), merge_sort(a, mid+1, r);

    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(a[i] <= a[j]) tmp[k++] = a[i++];
        else tmp[k++] = a[j++];
    }
    while(i <= mid) tmp[k++] = a[i++];
    while(j <= r) tmp[k++] = a[j++];

    for(int i = l, j = 0; i <= r; i ++, j ++) a[i] = tmp[j];
}

AcWing 785.快速排序
AcWing 786.第k个数

6快速排序（最快）

• 思想：分治，双指针，递归
• 注意：边界的选取，以防segmentation fault越界等问题

void quick_sort(int *a, int l, int r)
{
    if (l >= r) return ;

    int x = a[l+r>>1], i = l-1, j = r+1;
    while (i < j)
    {
        while (a[++ i] < x);
        while (a[-- j] > x);
        if (i < j) swap(a[i], a[j]);
    }
    quick_sort(a, l, j), quick_sort(a, j+1, r);
}

堆排序解析

7堆排序（须知此排序为使用了模拟堆，为了使最后一个非叶子节点的编号为n/2，数组编号从1开始）

void down(int *a, int u)
{
    int t = u;
    if (u<<1 <= n && a[u<<1] < a[t]) t = u<<1;
    if ((u<<1|1) <= n && a[u<<1|1] < a[t]) t = u<<1|1;
    if (u != t)
    {
        swap(a[u], a[t]);
        down(a, t);
    }
}

int main()
{
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = n/2; i; i -- ) down(a, i);
    while (true)
    {
        if (!n) break;
        cout << a[1] << ' ';
        a[1] = a[n];
        n -- ;
        down(a, 1);
    }
    return 0;
}

8计数排序

void counting_sort(int *a, int n)
{
    int sorted[N];
    int maxv = a[0];
    for (int i = 1; i < n; i ++ )
        if (maxv < a[i])
            maxv = a[i];
    int count[maxv+1];
    for (int i = 0; i < n; i ++ ) count[a[i]] ++ ;
    for (int i = 1; i <= maxv; i ++ ) count[i] += count[i-1];
    for (int i = n-1; i >= 0; i -- )
    {
        sorted[count[a[i]]-1] = a[i];
        count[a[i]] -- ;
    }
    for (int i = 0; i < n; i ++ ) a[i] = sorted[i];
}

9桶排序（基数排序是桶排序的特例，优势是可以处理浮点数和负数，劣势是还要配合别的排序函数）

vector<int> bucketSort(vector<int>& nums) {
    int n = nums.size();
    int maxv = *max_element(nums.begin(), nums.end());
    int minv = *min_element(nums.begin(), nums.end());
    int bs = 1000;
    int m = (maxv-minv)/bs+1;
    vector<vector<int> > bucket(m);
    for (int i = 0; i < n; ++i) {
        bucket[(nums[i]-minv)/bs].push_back(nums[i]);
    }
    int idx = 0;
    for (int i = 0; i < m; ++i) {
        int sz = bucket[i].size();
        bucket[i] = quickSort(bucket[i]);
        for (int j = 0; j < sz; ++j) {
            nums[idx++] = bucket[i][j];
        }
    }
    return nums;
}

10基数排序

int maxbit(int *a, int n)
{
    int maxv = a[0];
    for (int i = 1; i < n; i ++ )
        if (maxv < a[i])
            maxv = a[i];
    int cnt = 1;
    while (maxv >= 10) maxv /= 10, cnt ++ ;

    return cnt;
}
void radixsort()
{
    int t = maxbit();
    int radix = 1;

    for (int i = 1; i <= t; i ++ )
    {
        for (int j = 0; j < 10; j ++ ) count[j] = 0;
        for (int j = 0; j < n; j ++ )
        {
            int k = (a[j] / radix) % 10;
            count[k] ++ ;
        }
        for (int j = 1; j < 10; j ++ ) count[j] += count[j-1];
        for (int j = n-1; j >= 0; j -- )
        {
            int k = (a[j] / radix) % 10;
            temp[count[k]-1] = a[j];
            count[k] -- ;
        }
        for (int j = 0; j < n; j ++ ) a[j] = temp[j];
        radix *= 10;
    }

}