如图给出一个稀疏矩阵,要求表示出它的转置矩阵
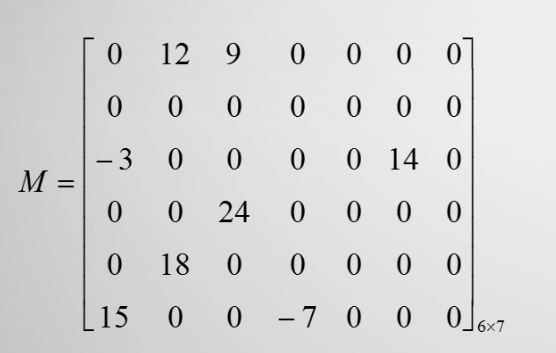
由这个矩阵我们能轻松得到它的三元组顺序表
| 6行(x坐标) | 7列(y坐标) | 8个元素 |
|---|---|---|
| 1 | 2 | 12 |
| 1 | 3 | 9 |
| 3 | 1 | -3 |
| 3 | 6 | 14 |
| 4 | 3 | 24 |
| 5 | 2 | 18 |
| 6 | 1 | 15 |
| 6 | 4 | -7 |
接下来我们同样把转置后的矩阵的三元组顺序表表示出来

| 7行(x坐标) | 6列(y坐标) | 8个元素 |
|---|---|---|
| 1 | 3 | -3 |
| 1 | 6 | 15 |
| 2 | 1 | 12 |
| 2 | 5 | 18 |
| 3 | 1 | 9 |
| 3 | 4 | 24 |
| 4 | 6 | -7 |
| 6 | 3 | 14 |
我们要如何才能通过第一个三元组顺序表得到第二个三元组顺序表呢
按照最简单的思路,我们一般会通过双重循环
朴素的双重循环
按照列坐标从头到尾遍历,遇到1的时候,将i j互换放入到第二个三元组顺序表第一个位置
按照这样的方法,每一次都有可能需要遍历n次,一共需要走n趟,时间复杂度会是O(n²)级别
那么有没有一种方法能一步到位呢
快速转置
为实现快速转置,我们引入==num==数组和==cpot==数组
num[col]:表示矩阵M中第col列中非零元个数
cpot[col]:指示M中第col列第一个非零元在转置后的三元组顺序表中位置
显然有:
cpot[1] = 1;
cpot[col] = cpot[col - 1] + num[col - 1]; //第col - 1列第一个非零元的位置加上第col - 1列非零元的个数
由此,我们能构建出col、num[col]、cpot[col]的一个表
| col | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| num[col] | 2 | 2 | 2 | 1 | 0 | 1 | 0 |
| cpot[col] | 1 | 3 | 5 | 7 | 8 | 8 | 9 |
这样我们遍历最开始的三元组顺序表
第一个列是2,我们查找 co l为 2 的 cpot[col] ,为 3,那么将原表第一行放入到转置后的第三个位置,同时 col 为 2 的 cpot[col] += 1
cpot[col] + 1 是因为若这一列还有非零元,那么肯定会是它的下一个位置
代码如下
Status FastTransposeSMatrix( TSMatrix M, TSMatrix &T ) {
// 采用三元组顺序表存储表示,求稀疏矩阵 M 的转置矩阵 T
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
if (T.tu) {
// mu行 nu列
for (col=1; col<=M.nu; ++col) num[col] = 0;
for (t=1; t<=M.tu; ++t) ++ num[M.data[t].j];
// 求 M 中各列非零元的个数
cpot[1] = 1;
for (col=2; col<=M.nu; ++col) cpot[col] = cpot[col -1] + num[col -1];
// 求 M 中各列的第一个非零元在 T.data 中的序号
for (p=1; p<=M.tu; ++p) { // 转置矩阵元素
col = M.data[p].j;
q = cpot[col];
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
++ cpot[col];
} // for
} // if
return OK;
} // FastTransposeSMatrix


跟我作业一样
#### 作业好像不是这样吧