2019年8月XX日线段树讲义

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

2019年8月XX日线段树讲义

作者：

秦淮岸灯火阑珊 , 2019-08-11 21:51:25 , 所有人可见 , 阅读 4522

74

62

线段树

算法理解

学习理由

线段树,是数据结构从入门到进阶的一条必经之路.

线段树,是高阶数据结构的基础.

线段树,是萌新到大佬的一个坎.

线段树,是代码量剧增的一个毒瘤.

线段树,是区间性质的集合体.

引入概念

线段树是什么

线段树,听上去挺高大上的,那么它实际上是什么呢?

一颗树.

这个概念似乎太笼统?

一颗树,上面的节点表示一个区间.

这个概念感觉不准确.

一棵树,上面的节点表示一个区间,父亲节点表示的区间是左右儿子相加.

这个概念看上去不完美.

一棵树,上面的节点表示一个区间,父亲节点表示的区间是左右儿子相加.

同一层的节点所代表的区间,相互不会重叠.一层节点所代表的区间，加起来是个连续的区间

看上去挺棒的,我们来一个线段树从无到有的动图,形象地理解一波.

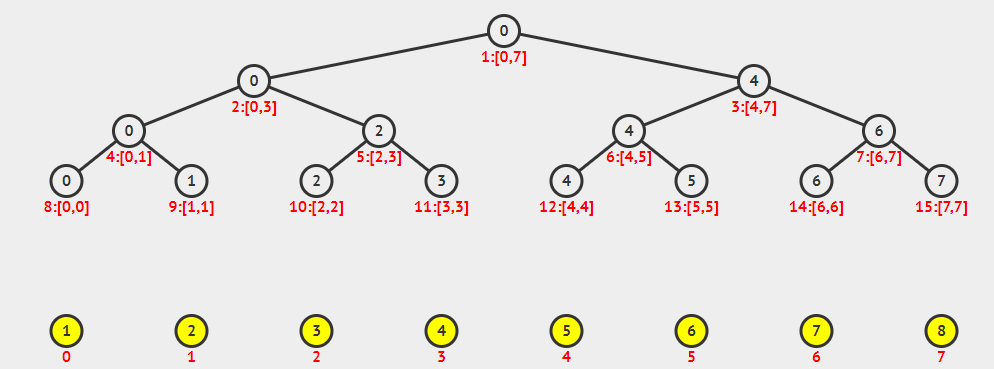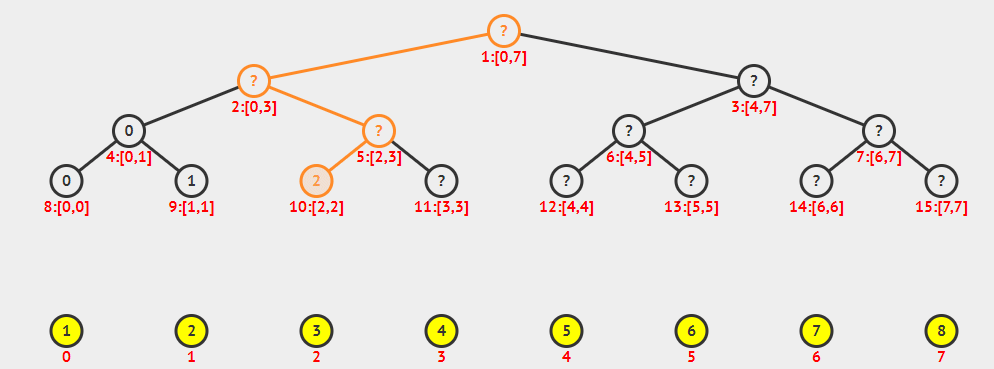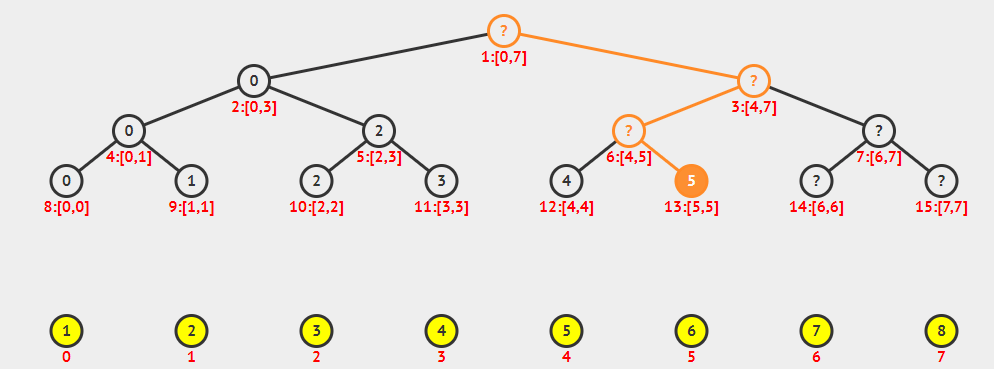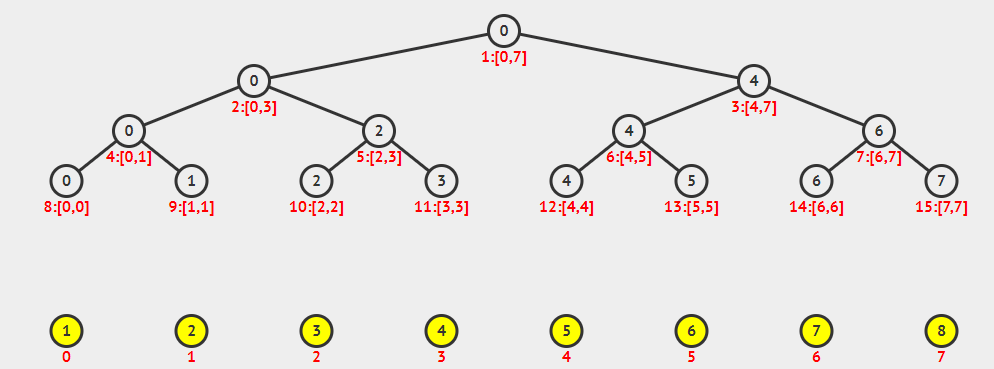
录制_2019_08_04_21_53_05_755.gif

看完这个动画,是不是有些初步理解呢?

我们接着来好好的分析一波概念.

线段树的操作

基本上大部分的区间操作,线段树统统都资瓷.

比如说:单点修改,单点查询,区间修改,区间查询,区间开方,区间四则运算.......

太多了,我们先搁在这里.

正经的概念

我们先拿出一棵线段树.

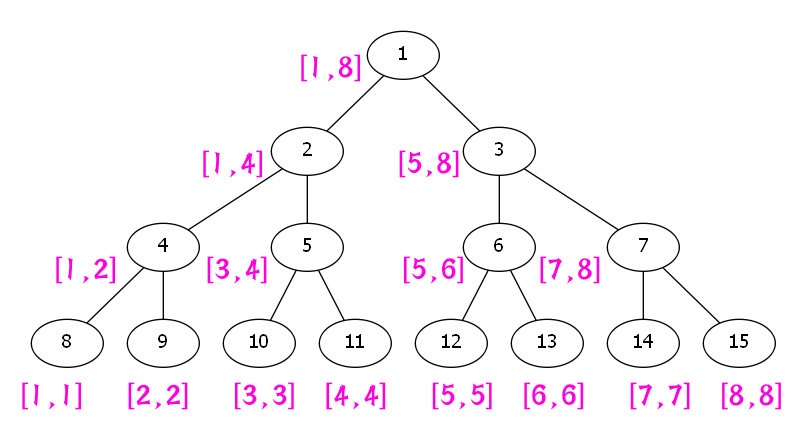
线段树1.png

这颗线段树,就是我们~~可爱的~~线段树.

此时Acwing小剧场开播了.

空间消耗

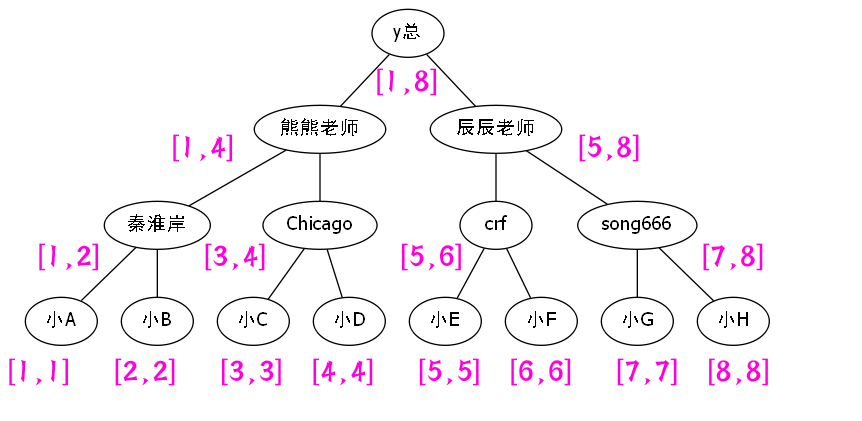
线段树3.png

观察这张图片,我们发现这个图片有管理关系.

每一层和下面一层,$节点个数 \times 2$

这告诉我们~~Acwing人很多.~~空间开销有点大.

那么一般是多大呢.
$$ 线段需求空间=最底层节点数 \times 4 $$
这是为什么啊,为什么一定要开这么大呢,是有什么证明吗?

层数	这一层节点个数	总和节点
$1$	$2^0$	$2^0$
$2$	$2^1$	$2^0+2^1$
$3$	$2^2$	$2^0+2^1+2^2$
$4$	$2^3$	$2^0+2^1+2^2+2^3$
$5$	$2^4$	$2^0+2^1+2^2+2^3+2^4$
$k$	$2^{k-1}$	$2^0+2^1+…+2^{k-1}$

观察最后一行.
$$ 2^0+2^1+2^2+2^3+…+2^{k-1} $$
这个式子是不是感觉似曾相识啊.
$$ 2^0+2^1+2^2+2^3+…+2^{k-1}=2^k-1 $$
那么我们再来看一下最后一层的节点个数
$$ 2^{k-1} $$
那么再来看一下理论上的节点数.
$$ 2^{k}-1=2*2^{k-1}-1 $$
这么说来我们只需要两倍内存就好了啊.

某位大佬的证明.

假设我们N个连续的节点需要建立线段树，如果最下层有节点，那么最左边一定不是空的。而最左边节点也就是左儿子是：$[l,(l+r)>>1]$。因此就是$(1+N)$不停$/2$。那么线段树的深度为$log_2{1+N}$

假如是满二叉树，那么节点数为
$$ 2^{log_2{1+N}} $$

线段树4n证明.png

区间概念

线段树为什么,很多人都觉得难以理解,其实很大程度上面,是人们对于新概念掌握不清楚,再加上线段树特别长的代码,是的很多人对于这类数据结构避而远之,称之为毒瘤.

其实线段树概念并不难以理解,我们只需要清楚一点,那就是.

线段树,树上面的所有节点都是线段,都是一个区间.

这个概念十分重要.

我们可以理解为y总节点,代表的不只是yxc一人,还有整个Acwing.

一个人代表的不再是一个人,而是这个人和这个人所拥有的一切.

好的,接下来.我们再来分析一下,儿子节点概念.

我们知道,在树上面,存在着父亲与儿子之间的关系,这种关系是一种上下级关系.

父亲就是父亲,儿子就是儿子,两者之间除了父子关系,没有了其他联系.

但是在线段树上面,父亲与儿子关系,又增加了一种包含与被包含的概念.

我们发掘一下这个线段树,很容易发现.

一个节点是$[l,r]$ ,那么它的左儿子节点为$[l,k]$ ,右儿子节点是$[k+1,r]$

这是什么意思?

我们发现一个父亲节点,完全可以被两个儿子合并在一块表示.

比如说我们现在要秦淮岸同学.

其实可以喊秦蒟蒻+秦学弟.

那么我们就像贴标签一样的,一个人表示为它的标签总和.

同理,我们同时也可以将两个儿子,用一个父亲表示.

比如说,当我们喊秦蒟蒻,秦学弟的时候,我们就知道,这个人就是秦淮岸灯火阑珊了.

总而言之,言而总之,没有什么是一个表格不能表示的概念的.

我们来一个表格表示一下。

定义	概念
节点	一个区间$[l,r]$
左儿子	一个区间$[l,r]$中的$[l,mid]$
右儿子	一个区间$[l,r]$中的$[mid+1,r]$

操作分析

~~终于到了，最好写，也最好复制代码的地方了。~~

宏定义操作

#define mid ((l+r)>>1) //mid中间点
#define Lson rt<<1,l,mid //根节点编号*2，区间[l,mid],左儿子表示
#define Rson rt<<1|1,mid+1,r //根节点编号*2+1，区间[mid+1,r]，右儿子表示

上传操作

void Push_up(int rt)
{
    sum[rt]=sum[rt<<1]+sum[rt<<1 | 1];//左右儿子节点和
}

建树操作

void build(int rt,int l,int r)//当前节点编号，左区间，右区间
{
    if (l==r)//叶子节点
    {
        sum[rt]=1;//sum数组，这里是区间和数组
        return ;
    }
    build(Lson);//左儿子
    build(Rson);//右儿子
    Push_up(rt);//左右儿子上传操作
}

单点修改

void Change(int rt,int l,int r,int x,int v)//x点权值修改成v
{
    if (l==r)//是叶子节点,同时也是目标位置
    {
        sum[rt]=v;//修改操作
        return ;
    }
    if (x<=mid)//左儿子上
        Change(Lson,x,v);
    else//右儿子身上
        Change(Rson,x,v);
    Push_up(rt);//左右儿子上传
}

区间查询

int Query_sum(int rt,int l,int r,int ql,int qr)//目标区间ql,qr,当前区间[l,r],当前节点是rt
{
    int ans=0;
    if (ql<=l && r<=qr) //目标区间包括了当前区间[l,r]
        return sum[rt];//直接返回当前区间
    if (ql<=mid) //目标区间有部分在当前区间的左边
        ans+=Query_sum(Lson,ql,qr);
    if (qr>mid)//目标区间有部分在当前区间的右边
        ans+=Query_sum(Rson,ql,qr);
    Push_up(rt);
    return ans;
}