前言

此前在帮人整理题解的时候，提高篇二分图部分的四个匹配问题中，我将“网络最大流”这一概念带入了题解中，并且比较细致的介绍了常见的Edmons-Karp算法和Dinic算法，而在前不久，评论区中有人提到了ISAP算法，这一略显冷门，却在一般图上比Dinic更高效的算法，下面将以二分图匹配问题为切入点，浅谈包括ISAP在内的“增广路”型网络流算法在二分图匹配问题中的性能表现
本帖中代码全都用C++实现

网络最大流概述

网络最大流最开始的定义为：求解如何充分利用装置的能力，使得运输流量达到最大，效果最好。既然要求解最大流量，那首先要定义“网络”，下面给出网络$(Net)$基类的定义：

//网络图基类，每一种算法都要使用它包含的信息
class Net {
protected:
    /*
    * 存储方式统一为链式前向星
    * fin表示每条边的终点
    * val表示每条边的最大容量
    * last表示每个节点邻接的边中最后被连上的边序号
    * nxt表示每条边在遍历顺序中的后继边序号
    * 整个链式前向星存储结构相当于带边索引的邻接表
    * 比邻接矩阵省空间，比一般邻接表多了对任意边的直接存取
    * 索引从2开始，便于取得反向边
    * source和terminal分别为网络的源点（始端）和汇点（终端）
    */
    vector<int> fin, last, nxt;
    vector<long long> val;
    int tot = 2, source = 0, terminal = 0;

    //单向连接两个节点，即生成一条边
    void connect(int s, int e, int v) {
        //tot即为当前索引值
        fin[tot] = e;
        val[tot] = v;
        /*
        * 以下表明新索引总是被加入到遍历顺序的最前方
        * 遍历顺序形似单向链表（链式前向星因此得名）
        */
        nxt[tot] = last[s];
        last[s] = tot++;
    }
public:
    Net() {}
    Net(int _n, int _m, int _s, int _t) {
        source = _s;
        terminal = _t;
        //关于边信息的表长度都需要达到边数的两倍，以存放反向边
        fin.resize(2 * _m + 10);
        val.resize(2 * _m + 10);
        last.resize(_n + 5);
        nxt.resize(2 * _m + 10);
        int s, e, v;
        while (_m--) {
            cin >> s >> e >> v;
            //反向边容量为0，事先设定好
            //如此能保证从2开始偶数索引表示正向边，奇数索引表示反向边
            connect(s, e, v);
            connect(e, s, 0);
        }
    }

    //基类Net为抽象类，纯虚函数getMaxFlow需要在具体用算法实现的时候重写
    virtual long long getMaxFlow() = 0;
};

基类只提供成员变量和成员函数定义，其实现即最大流量的求解交给由它继承而来的各个实现类，链式前向星结构为$protected$即保护权限，使得子类可以访问基类中的这些成员

算法概述

接下来给出重要定义“增广路”：从源点到汇点，每条边的剩余容量都大于0的路径
以及基于这个定义给出的EK算法和Dinic算法
EK算法的原理和邻接矩阵实现在题解 机器任务(EK算法) 中提到过，这里给出它的链式前向星实现类：

class EKNet : public Net {
private:
    //vis表示访问情况，pre和邻接矩阵不同，存储的是前驱边的索引值
    //EK算法实现类不需要作为其他类的基类，因此没有protected成员
    vector<int> vis, pre;

    //找增广路（从源点到汇点）
    bool findPath() {
        queue<int> q;
        fill(pre.begin(), pre.end(), 0);
        fill(vis.begin(), vis.end(), 0);
        q.push(source);
        vis[source] = 1;
        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            for (int i = last[cur]; i != 0; i = nxt[i]) {
                int nx = fin[i];
                //可增广的条件是目标节点未被访问，且其中连接的那条边容量大于0
                if (vis[nx] == 0 && val[i] > 0) {
                    vis[nx] = 1;
                    pre[nx] = i;
                    //找到汇点可以直接判true
                    if (nx == terminal) return true;
                    q.push(nx);
                }
            }
        }
        return false;
    }
public:
    EKNet() {}
    //实现类构造函数需要首先调用基类构造函数，将网络图构造出来
    EKNet(int _n, int _m, int _s, int _t) : Net(_n, _m, _s, _t) {
        vis.resize(_n + 5);
        pre.resize(_n + 5, -1);
    }

    long long getMaxFlow() {
        long long sum = 0;
        //EK算法特点：每次只找一条增广路
        while (findPath()) {
            int now = terminal, e = 0;
            long long mf = INF;
            //由汇点向源点通过事先建立的反向边回溯
            while (now != source) {
                e = pre[now];
                mf = min(mf, val[e]);//确定此路径上可以产生的最大流量（木桶短板原理）
                now = fin[e ^ 1];//取得反向边的终点，即前驱节点
            }
            sum += mf;
            now = terminal;
            //第二次回溯，修改正反向边的容量，累加流量
            while (now != source) {
                e = pre[now];
                val[e] -= mf;
                val[e ^ 1] += mf;
                now = fin[e ^ 1];
            }
        }
        return sum;
    }
};

由此也可见得，索引从2开始计数的好处，对于每一个偶数索引，其对应边的反向边索引要+1，而奇数索引反向边的索引则要-1，这个分类讨论可以用$xor~1$来简化
下面的Dinic算法同理（介绍帖为 棋盘覆盖(Dinic算法) ：

class DinicNet : public Net {
protected:
    //ISAP需要通过Dinic算法继承而来
    vector<int> depth;
private:
    //Dinic算法为节点赋予层级，从源点开始，能为汇点赋上层级就说明增广成功
    bool findPath() {
        fill(depth.begin(), depth.end(), 0);
        depth[source] = 1;
        queue<int> q;
        q.push(source);
        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            for (int i = last[cur]; i != 0; i = nxt[i]) {
                int nx = fin[i];
                //可赋予层级条件：后继节点未赋予层级，并且到达该节点的边容量大于0
                if (val[i] > 0 && depth[nx] == 0) {
                    depth[nx] = depth[cur] + 1;
                    //和EK算法一样，遇到汇点就停
                    if (nx == terminal) return true;
                    q.push(nx);
                }
            }
        }
        return false;
    }

    //发送流量的函数是递归的，可以向某个节点的所有后继节点一同发送流量（增广多条边）
    long long sendFlow(int cur, long long rest = INF) {
        if (cur == terminal) return rest;//到汇点了，无法继续往后
        long long sum = 0;
        for (int i = last[cur]; i != 0; i = nxt[i]) {
            int nx = fin[i];
            //流量发送不能越级
            if (val[i] > 0 && depth[nx] == depth[cur] + 1) {
                //向后继节点发送流量
                long long mf = sendFlow(nx, min(val[i], rest - sum));
                //一样是修改正反边容量，并累加
                val[i] -= mf;
                val[i ^ 1] += mf;
                sum += mf;
            }
        }
        return sum;
    }
public:
    DinicNet() {}
    DinicNet(int _n, int _m, int _s, int _t) : Net(_n, _m, _s, _t) {
        depth.resize(_n + 5);
    }

    long long getMaxFlow() {
        long long sum = 0;
        //这里类似于EK算法，能增广就从源点发送流量并累加
        while (findPath()) sum += sendFlow(source);
        return sum;
    }
};

此前已做过说明，二分图问题上EK算法的理论时间复杂度是$O(n\*m^2)$，Dinic算法是特有的$O(\sqrt{n}\*m)$而非一般图中的$O(n^2\*m)$，一般图上Dinic略微占优，但是二分图上Dinic是绝对占优的

最后来到ISAP算法，该算法是基于Dinic，旨在一般网络图上得到比Dinic算法更好的表现而产生的，那么对于二分图上明显占优的Dinic算法，它能否在Dinic擅长的领域击败Dinic呢？首先来看ISAP实现类（继承自Dinic实现类$DinicNet$而非基类$Net$）：

class IsapNet : public DinicNet {
private:
    vector<int> gap;//用来记录各个层级上节点的数量（其实我不太理解为什么要叫gap）
    bool status_blocked = false;//判断是否阻塞

    //与Dinic算法不同，它是从汇点反向赋予层级
    void setDepth() {
        fill(depth.begin(), depth.end(), 0);
        fill(gap.begin(), gap.end(), 0);
        queue<int> q;
        q.push(terminal);
        depth[terminal] = 1;
        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            for (int i = last[cur]; i != 0; i = nxt[i]) {
                int pr = fin[i];//向源点遍历，按照逻辑关系应该是前驱pr而不是后继nx
                if (depth[pr] != 0) continue;
                //ISAP特点：不检查途径边容量
                q.push(pr);
                depth[pr] = depth[cur] + 1;
                gap[depth[pr]]++;//统计该层级节点数量
            }
        }
    }

    long long sendFlow(int cur, long long rest = INF) {
        //前面跟Dinic算法完全一样
        if (cur == terminal) {
            return rest;
        }
        long long sum = 0;
        for (int i = last[cur]; i != 0; i = nxt[i]) {
            int nx = fin[i];
            if (val[i] > 0 && depth[nx] == depth[cur] - 1) {
                long long mf = sendFlow(nx, min(val[i], rest - sum));
                //这里是Dinic算法的另一种写法，当前流量大于0才修改，累加和达到余量就可以直接返回
                if (mf > 0) {
                    val[i] -= mf;
                    val[i ^ 1] += mf;
                    sum += mf;
                }
                if (sum == rest) return sum;
            }
        }
        /*
        * 不一样的地方来了
        * 此处可以保证当前节点向所有后继节点发送流量之后
        * 余量仍然大于0
        * 这时就要把当前节点升高一层
        * 将后继节点分离开
        */
        int& d = depth[cur];
        gap[d]--;//先修改gap再升高cur的层级数
        if (gap[d] == 0) {
            /*
            * 这时已经不存在层级数为d的节点
            * 根据Dinic算法继承而来的“不能越级”原则
            * 一旦出现了断层，就无法继续增广了
            * 就是所谓的“阻塞”现象
            */
            status_blocked = true;
        }
        d++;//由于引用的特性，表中的层级数也会被一起修改
        gap[d]++;//升高一级后，对应的层级数节点+1
        return sum;
    }
public:
    IsapNet() {}
    IsapNet(int _n, int _m, int _s, int _t) : DinicNet(_n, _m, _s, _t) {
        gap.resize(_n + 5);
    }

    long long getMaxFlow() {
        long long sum = 0;
        setDepth();
        while (!status_blocked) sum += sendFlow(source);
        return sum;
    }
};

ISAP相比Dinic，只用了一次bfs，修改层级都在dfs的过程中进行，因此在一般图上比Dinic省事。对比一下在 洛谷P3376 上普遍最耗时的Case 9中的测试情况：EK用时986ms，Dinic用时107ms，ISAP用时92ms

二分图特例实验

前述已经备至，一般图上ISAP是最快的，接下来就来生成一组二分图性质的数据，两部分都是100个节点，中间的边数为5000，用这样一组数据来测试ISAP和Dinic（EK不用测了，想想都知道肯定慢）
生成数据的代码段先展示，生成程序保证图中没有重边和自环，且具备随机性：

#include <iostream>
#include <fstream>
#include <format>
#include <random>
using namespace std;

default_random_engine dre(static_cast<unsigned int>(time(nullptr)));
int** mat;
ofstream ofs;

int main() {
    int n, m;
    cin >> n >> m;
    mat = new int* [n + 1];
    for (int i = 0; i <= n; i++) mat[i] = new int[n + 1](0);
    ofs.open("input.txt", ios::trunc | ios::out);
    ofs << format("{} {} {} {}", 2 * n + 2, m + 2 * n, 2 * n + 1, 2 * n + 2) << endl;
    for (int i = 1; i <= n; i++) ofs << format("{} {} 1\n{} {} 1", 2 * n + 1, i, n + i, 2 * n + 2) << endl;
    uniform_int_distribution ud(1, n);
    while (m > 0) {
        int s = ud(dre), e = ud(dre);
        if (mat[s][e] == 1) continue;
        m--;
        mat[s][e] = 1;
        ofs << format("{} {} 1", s, n + e) << endl;
    }
    for (int i = 0; i <= n; i++) delete[] mat[i];
    delete[] mat;
    return 0;
}

以此生成了10组数据，分别用Dinic算法和ISAP算法跑，得到以下结果：

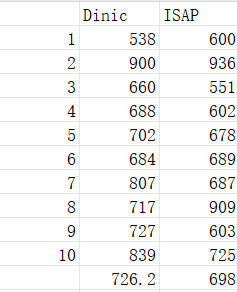
（单位：微秒）
ISAP以微小优势胜过了Dinic，可见就算是Dinic的长处二分图，ISAP仍然能险胜（毕竟青出于蓝而胜于蓝嘛

结论

ISAP算法在时间效率上，各方面都胜过Dinic（虽然二分图上优势比较微小），而对于提高篇的二分图匹配问题，ISAP确实是比Dinic更优选的算法