我记得c++y总图论搜索模板是公开的 所以我想发一下py3版应该也没问题 慢慢汇总中

$\underline{基础算法模板}$	数据结构模板	有猷de数学知识,第四章	Dynamic Programming思路
			一行多个emoji

按照实际图论问题分：

$\huge\color{red}{【最短路问题】}$：
①Dijkstra 初始化距离∞ 迭代不在集合中距离最小的编号，加入集合。
② Bellman-ford
③ Spfa (队列优化的②)
④ Floyd
$\huge\color{red}{【最小生成树问题】}$：
①Prim $O(N^2)或堆优化O(MlogN)$②Kruskal $O(MlogM)$

$\huge\color{red}{【二分图】}$：① 染色图 (即深度优先遍历$\underline{DFS}~ O(N+M)$) ②匈牙利算法 【求二分图最大分配】 $O(MN)$

$\huge \color{#00ccff}{\textbf{【树与图的存储】}}$
树Tree是一种特殊的图Graph，与图的存储方式相同。
对于$\underline{\textbf{无向图}}$中的边xy，存储两条有向边x->y, y->x。 因此我们可以只考虑有向图的存储。

(1) 邻接矩阵：g[x][y] 存储边x->y
(2) 邻接表：…

# 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
idx = 0
e, ne, h = [0] * M, [0] * M, [-1] * N

# 添加一条边x->y
def add(x, y):
    global idx
    e[idx] = y
    ne[idx] = h[x]
    h[x] = idx
    idx += 1

题外话：觉得思路可以是$\color{red}{红色}$,$\textbf{粗体}$,$\underline{\color{green}{醒}\color{yellow}{目}}$，而区分于代码块

以下图论与搜索 模板

1. DFS 深搜

左边一条路走到黑

def dfs(u):
    #当所有坑位被占满 那么输出储存的路径
    if u == n:
        for i in range(0,n):
            print(path[i], end = " ")
        print('')
    #另一种(几乎)等价写法ans.append(' '.join(list(map(str, path))))
    #从1到n遍历寻找第u个位置可以填的数
    for i in range(1, n+1):
        #确认数字状态，是否已经被使用 如果没有被占执行下面操作
        if not state[i]: #等价于state[i]是[False]
            path[u] = i #在坑位上填上次数字
            state[i] = True #标注数字状态，已经被使用
            dfs(u+1) #进入下一层
            state[i] = False #回溯恢复数字状态

2. BFS 宽搜

一层一层搜

bfs模板：

"""1. 初始化队列
2. while queue不为空
>  3. 队顶元素出队
>  4. 遍历，满足条件的入队"""

def bfs():
    queue = [1]
    st[1] = True
    d[1] = 0
    while queue:
        t = queue.pop(0)
        if t not in graph: continue

        for i in graph[t]:
            if not st[i]:
                st[i] = True
                queue.append(i)
                if d[i]==-1:
                    d[i] = d[t]+1
    print(d[n])  

3. 拓扑排序 —— 模板题 AcWing 848. 有向图的拓扑序列

def topSort():
    global res
    # 1. 初始化队列：入度为零时，节点入队
    queue = []
    for i in range(1,n+1):
        if d[i]==0:
            queue.append(i)
            res.append(i)
    # 2. while queue不为空
    while queue:
        # 3. 队头元素出队
        t = queue.pop(0)
        # 4. 有向图判断t节点是否出度为0(出度为0的点不在graph的keys中)
        if t not in graph: continue
        # 5. 循环遍历满足条件的节点入队:入度为1的节点，删掉节点t后入度变为0，所以条件为入度d[j]==1
        for j in graph[t]:
            if d[j]-1==0:
                queue.append(j)
                res.append(j)
            else:
                d[j] -= 1
    return len(res)==n    # !!!出错：如果只返回res的话，那么有环图返回的res包含的节点会小于n

【最短路问题】 图源自鹿

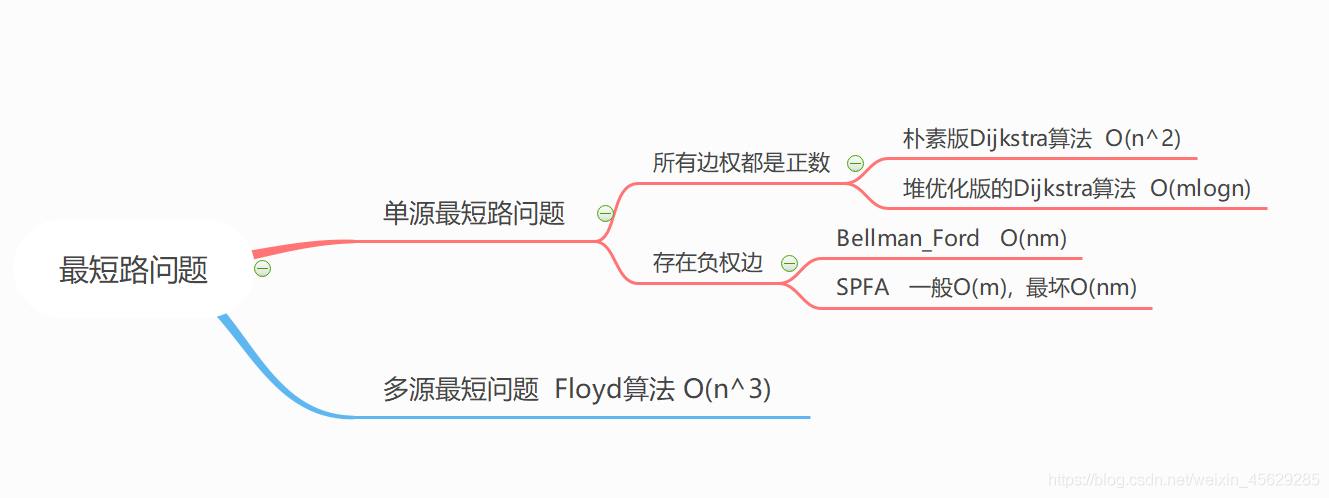
4. 朴素dijkstra算法 —— 模板题 AcWing 849. Dijkstra求最短路 I

迪杰特斯拉算法求解单源最短路问题, 有向图和无向图均可求解

def dijkstra():
    dist = [float("inf") for i in range(n+1)]    # 存储每个点到节点1的最短距离
    dist[1] = 0
#     st[1] = True    # ！！！出错：应该放到下一行的循环里，去寻找与节点1距离最近的点，否则第一轮循环找到的t=2，而dist[2]是正无穷
    for i in range(1, n+1):
        t = 0    # 在还未确定最短路的点的集合中，寻找距离最小的点
        for j in range(1, n+1):
            if st[j]==False and ((t==0) or dist[j]<dist[t]):
                t = j
        st[t] = True
        # 用t更新其他点的距离
        for j in range(1, n+1):
            if dist[j]>dist[t]+graph[t][j]:
                dist[j] = dist[t]+graph[t][j]
    if dist[n]==float("inf"):
        return -1
    else:
        return dist[n]

5. Bellman-Ford算法 —— 模板题 AcWing 853. 有边数限制的最短路

$\color{red}{Bellman-Ford算法，解带负权边的有向图和不带负权边的无向图的单源}$

"""步骤： 1.控制最短路的最大边数；2. 遍历图的所有边"""

def bellmanFold():
    dist = [float("inf") for i in range(n+1)]
    dist[1] = 0
    for i in range(0,k):    # 1.控制最短路的最大边数
        distCopy = dist.copy()    # 注意，在求有边数限制的最短路时，一定要对dist进行备份，以防止在后面遍历边时出现串联问题
        for x,y,z in edge:    # 2. 遍历图的所有边
            if dist[y]>distCopy[x]+z:
                dist[y] = distCopy[x]+z
    if dist[n]>= float("inf")/2.0:
        return -1
    else:
        return dist[n]

6. SPFA算法模板：（队列优化的Bellman-Ford算法）AcWing 851. spfa求最短路

基本思想：
 """用队列优化Bellman-Fold算法，长得有点像堆优化的Dijkstra算法
    在a->b的边中，Bellman-Fold算法的更新公式为：dist[b] = min(dist[b], dist[a]+weight),若想dist[b]变小，则dist[a]一定需要变小"""

SPFA算法模板：

def spfa():
    dist = [float("inf") for i in range(n+1)]
    dist[1] = 0
    queue = [1]
    st[1] = True    # ！！！注意，st数组用来标记节点i是否在queue中

    while queue:
        t = queue.pop(0)
        st[t] = False
        if t not in graph: continue

        for weight, node in graph[t]:
            if dist[node]>dist[t]+weight:    # !!!注意：判断dist[t]是否变小，变小则更新距离，同时将node添加到队列中
                dist[node] = dist[t] + weight
                if st[node]==False:    # node不在队列中
                    queue.append(node)
                    st[node] = True

    if dist[n]>=float("inf")/2:
        return -1
    else: 
        return dist[n]

7. floyd算法 —— 模板题 AcWing 854. Floyd求最短路

"""基本思想："""
Floyd算法模板：
n, m, k = map(int, input().split())

# 邻接矩阵存储图的模板
graph = [[float("inf") for i in range(n+1)] for j in range(n+1)]    # 邻接矩阵存稠密图
for i in range(1, n+1):    # 处理自环：正权边的自环一定不是最短路，所以初始化i到i的权重为0
    graph[i][i] = 0
while m:
    x,y,z = map(int, input().split())
    graph[x][y] = min(graph[x][y], z)    # 处理重边：保留重边中权重最小的边
    m-=1

算法结束后，graph[x][y]表示x到y的最短距离

def Floyd():
    for k in range(1,n+1):
        for i in range(1, n+1):
            for j in range(1,n+1):
                graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])

8. Prim 算法 —— 模板题 AcWing 858. Prim算法求最小生成树

时间复杂度是 $O(n^2+m)$, $n$ 表示点数，$m$ 表示边数

"""普利姆算法求解最小生成树输入为边列表，每条边表示为(起点，终点，权重)
   返回最小生成树权重总和，以及最小生成树边列表, 生成不了最小生成树返回None"""

def prim():
    dist = [float("inf") for i in range(n+1)]    # 记录每个结点到连通块的距离
    st = [False for i in range(n+1)]    # 标记节点是否在连通块中
    res = 0

    for i in range(1, n+1):
        t = 0
        for j in range(1,n+1):    # 未访问过的寻找距离连通块距离最近的节点
            if st[j]==False and (t==0 or dist[t]>dist[j]):
                t = j

        if t==0 and dist[t]==float("inf"): return float("inf")    # 如果上面的for循环没有找到距离连通块最近的点
        if t!=1:    # 如果节点t不是第一个点，就将t到连通块的距离加到res中；！！！注意，res的加和操作一定放在更新距离操作之前，否则加和一定是0
            res += dist[t]
        for j in range(1,n+1):   # 更新所有节点到连通块的距离，其中dist[t]更新为0
            dist[j] = min(dist[j], graph[t][j])
        st[t] = True
    return res

9. Kruskal算法 —— 模板题 AcWing 859. Kruskal算法求最小生成树

时间复杂度是 $O(mlogm)$, $n$ 表示点数，$m$ 表示边数

def find(x):
    """并查集的模板"""
    if p[x]!=x:
        p[x] = find(p[x]) #保存父节点
    return p[x]

def kruskal():
    res = 0    # 存储最小权重和
    cnt = 0    # 存储当前连通块的边数
    edges.sort(key=lambda s:s[2])    # 1. 对所有边按照权重升序排序

    for a,b,w in edges:    # 2. 遍历所有边，如果边的两个节点不连通，就将这两个点添加到并查集的集合中
        if find(a)!=find(b):
            p[find(a)] = find(b)
            res += w
            cnt += 1
    if cnt==n-1:    # !!!出错：不能写成if cnt>n-1，因为没有考虑不存在连通图的情况
        return res
    return False

10. 染色法判别二分图 —— 模板题 AcWing 860. 染色法判定二分图

$O(m+n)$ m点数，n边数

初始化

N, M = 100010,200010
n, m = map(int, input().split()) # n表示点数 m表示边数
e, ne, h = [0] * M, [0] * M, [-1] * N # 邻接表存储图
st = [0] * N
idx = 0
q = queue.Queue()

$x \rightarrow y$ # x 指向 y 见此页最上add(x,y)

BFS 版 AC

def bfs(i):
    q.put([i, 1])
    st[i] = 1
    while not q.empty():
        u, c = q.get()
        i = h[u]
        while i != -1:
            j = e[i]
            if not st[j]:
                st[j] = 3 - c
                q.put([j, 3 - c])
            elif st[j] == c:
                return False
            i = ne[i]
    return True

def solution():
    for _ in range(m):
        x, y = map(int, input().split())
        add(x, y)
        add(y, x)
## check() 函数
    flag = True
    for i in range(1, n + 1):
        if not st[i]:
            if not bfs(i):
                flag = False

    print("Yes") if flag else print("No")

DFS爆栈版

11. $\color{pink}{匈牙利算法}$

时间复杂度是 $O(nm)$, $n$ 表示点数，$m$ 表示边数

"""基本思想}"""：

def find(x):    # x表示左半部分第x号点
    for j in graph[x]:    # 遍历与左半部分x号点相连的右半部分的节点
        if st[j]==False:
            st[j]=True
            if match[j]==0 or find(match[j]):    # 如果右半部分的第j号点没有与左半部分匹配或者 与右半部分的第j号点匹配的左半部分的点可以匹配其他点
                match[j] = x
                return True
    return False

待续

Credit: Actor丶 皓佬
没提前问过，不知道可不可以post…侵删