题目描述

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。
简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例

Yes
No
No

题目分析

PAT上一道比较综合的问题，涉及到建立二叉搜索树，比较两棵树是否为同一棵树的问题。
为了更直观直观写了一个show()函数来显示两棵树的结构。

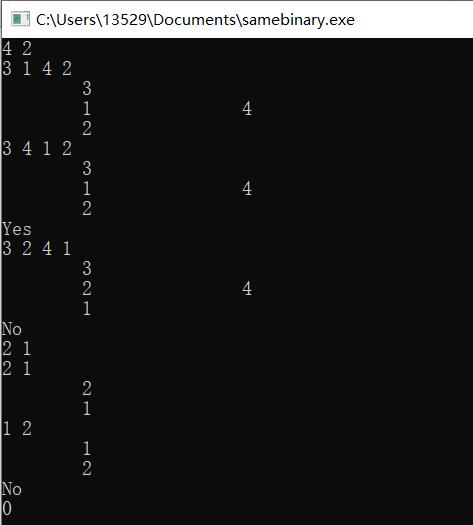
C++ 代码

#include<bits/stdc++.h>
using namespace std;
struct node
{
    int val;
    node *left;
    node *right;
    node(int x) : val(x), left(NULL), right(NULL) {}
};

node *root,*croot,*nullroot;
node *build(node *tnode,int tval);
void show(node *root);
bool sametree(node *root,node *croot);

int main()
{
    int n,l;
    while(1)
    {
        cin>>n;
        if(n==0) break;
        else{
            cin>>l;
            int x;
            root=nullroot;
            for(int i=0;i<n;i++)
            {
                cin>>x;
                root = build(root,x);
            }
            show(root);
            while(l--)
            {
                croot=nullroot;
                for(int i=0;i<n;i++)
                {
                    cin>>x;
                    croot = build(croot,x);
                }
                show(croot);
                if(sametree(root,croot)) cout<<"Yes"<<endl;
                else cout<<"No"<<endl;
            }
        }
    }
    return 0;
} 
node *build(node *root,int tval)
{
     if (!root) {
            node* ans = new node(tval);
            return ans;
        }
        if (tval < root->val) root->left = build(root->left, tval);
        else root->right = build(root->right, tval);
        return root;
}
void show(node *root)
{
    if(!root)
    {
        cout<<"empty";
        return ;
    }
    queue<node*> q;
    q.push(root);
    int co;
    while(q.size())
    {
        co=q.size();
        for(int i=0;i<co;i++)
        {
            node *t=q.front();
            q.pop();
            printf("%d ",t->val);
            if(t->left) q.push(t->left);
            if(t->right) q.push(t->right);
        }
        cout<<endl;
    }
}
bool sametree(node *root,node *croot)
{
    if(!root && !croot) return true;
    if(!root || !croot) return false;
    if(root->val == croot->val)
    {
        return sametree(root->left,croot->left) && sametree(root->right,croot->right);
    }
    else return false;
}