方法1：递推
复杂度 O(n^2)
算法思路：已知公式 C(m,n) = C(m-1,n) + C(m-1,n-1) , 运用DP思想直接地递推出结果。

代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;

const int N=2010,mod=1e9+7;

int c[N][N];

void init()
{
    for(int i=0;i<N;i++)
        for(int j=0;j<=i;j++)
            if(!j) c[i][j]=1;
            else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}

int main()
{
    init();

    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,b;
        scanf("%d%d",&a,&b);

        cout<<c[a][b]<<endl;
    }

    return 0;
}

方法2：预处理阶乘法
时间复杂度 O(NlogN)
算法思路：运用公式 C(m,n) = m!/n!/(m-n)! ，先预处理出1~N的阶乘和阶乘的乘法逆元。
（注意，这里需要mod是质数，一般是1e9+7，就可以直接运用费马小定理处理出乘法逆元。）
代码如下：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;

typedef long long LL;

const int N=1e5+10,mod=1e9+7;

int fact[N],infact[N];

int qmi(int a,int k,int p)
{
    int res=1;
    while(k)
    {
        if(k&1) res=(LL) res*a%p;
        a=(LL)a*a%p;
        k>>=1;
    }
    return res;
}

int main()
{
    fact[0]=infact[0]=1;
    for(int i=1;i<N;i++)
    {
        fact[i]=(LL)fact[i-1]*i%mod;
        infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;
    }

    int n;
    scanf("%d",&n);

    while(n--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d\n",(LL)fact[a]*infact[b]%mod*infact[a-b]%mod);
    }

    return 0;
}

方法3：运用卢卡斯定理
时间复杂度：递归算法，玄学复杂度，不过应该不慢。
算法思路：带入卢卡斯公式，递归调用，得到结果。注意本算法也需要用费马小定理求逆元。而且还要有直接求组合数的函数C。
代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;

typedef long long LL;

int qmi(int a,int k,int p)
{
    int res=1;
    while(k) 
    {
        if(k&1) res=(LL)res*a%p;
        a=(LL)a*a%p;
        k>>=1;
    }
    return res;
}

int C(int a,int b,int p)
{
    if(b>a) return 0;

    int res=1;
    for(int i=1,j=a;i<=b;i++,j--)
    {
        res=(LL)res*j%p;        //这么写可以直接在分子上乘到 (a-b)! ，分母只有一项。
        res=(LL)res*qmi(i,p-2,p)%p;
    }
    return res;
}

int lucas(LL a,LL b,int p)
{
    if(a<p && b<p) return C(a,b,p);
    return (LL)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        LL a,b;
        int p;
        cin>>a>>b>>p;
        cout<<lucas(a,b,p)<<endl;
    }

    return 0;
}

方法4：分解质因子法

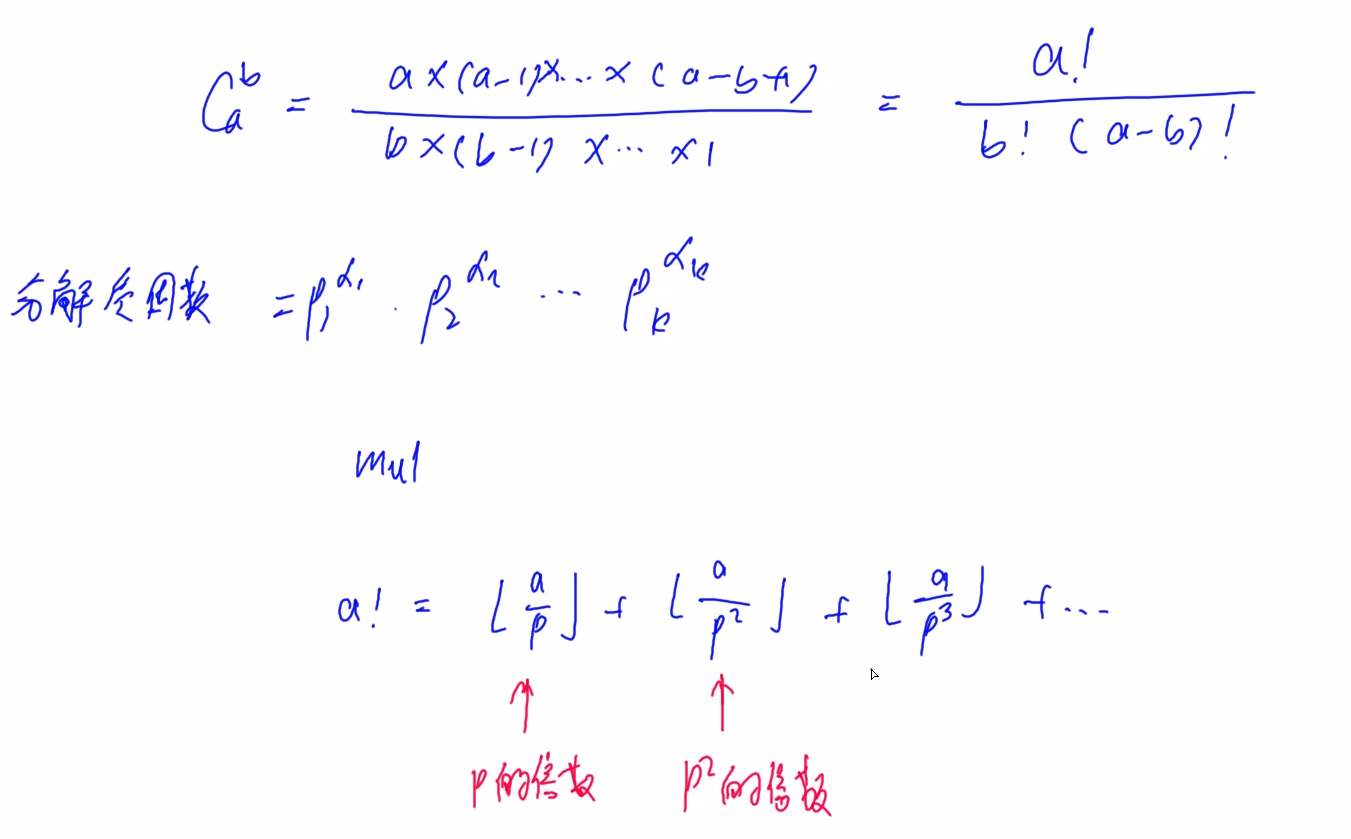
时间复杂度： O(NlogN)
算法思路：将分子分母的质因数都分解后消去，存在数组中(sum[i])，运用高精度乘法算出结果。这里需要有get函数来计算阶乘的质因子。
这里的分解质因数是直接对n!分解质因数，而不是对n分解，算法大致如上图。
代码如下：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;


const int N = 5010;

int primes[N], cnt;
int sum[N];
bool st[N];


void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}


int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }

    vector<int> res;
    res.push_back(1);

    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);

    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

小结：
这四种算法中，卢卡斯定理的时间复杂度是不确定的，但是他的数据范围是很有特点的。
如果是大数的组合数(1e18)一般选择卢卡斯定理。
而2、4算法时间复杂度相似，区别在于是否取余。
1的话只是好理解，要求不高的时候也可以写，比较简单。（雾）