T1
题目描述
有一棵二叉树,树上的叶子节点定义为“樱桃”。现在需要找出树上有多少个满足如下结构的“樱桃”串,即一串上刚好有两颗“樱桃”。
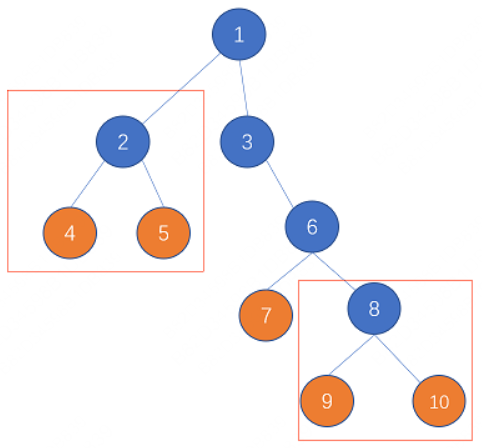
比如如下的一棵树,红框标示的有两个符合要求的结构,答案就是2
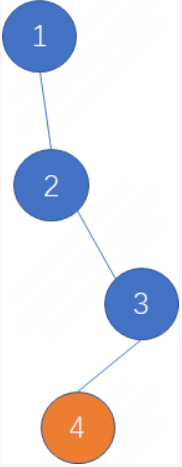
又比如下面的这棵树,没有任何符合要求的子结构,则答案是0
输入描述
第一行两正整数$m$,$n$,空格分开,分别代表总共有树上多少个节点,和树上有多少条边,$2 \leq m \leq 100$,$1 \leq n < 100$
下面有$n$行,每行为3个部分,用空格分割,第一个数字为某非叶子节点的id,
第二个为该边left还是right,第三个为子节点的id
注意:节点id彼此不会重复,id 1为根节点
输出描述
一个整数,标示符合要求的子结构的数量
示例1
样例输入
10 9
1 left 2
1 right 3
2 left 4
2 right 5
3 right 6
6 left 7
6 right 8
7 left 9
7 right 10
样例输出
2
说明
如题目说明的第一个样例图,可以看到,2-4-5串,8-9-10子串,两个子串符合条件,所以答案为2
算法
(哈希表模拟树) $O(n + m)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
int n, m, ret;
unordered_map<int, PII> S;
int main() {
cin >> n >> m;
while (m -- ) {
int a, b; string op;
cin >> a >> op >> b;
if (op == "left") S[a].first = b;
else if (op == "right") S[a].second = b;
}
for (int i = 1; i <= n; i ++ )
if (S.count(i) && S[i].first && S[i].second && !S.count(S[i].first) && !S.count(S[i].second))
ret ++ ;
cout << ret;
return 0;
}
T2
题目描述
给定一个字符s,问该字符串里有多少个长度大于1的子串都是回文?回文:正序的文本内容与倒序的文本内容相同,比如aa,aba
输入描述
字符串$s$,$1 \leq length(s) \leq 100000$
输出描述
一个整数,该字符串内部有多少个子串都是回文
示例1
样例输入
a
样例输出
0
说明
没有长度大1的回文
示例2
样例输入
abbcbb
样例输出
4
说明
解释:bb,bbcbb,bcb,bb
算法
() $O()$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
struct Node {
int len, sufflink, num;
int next[26];
} tree[N];
int len, num, suff;
string s;
LL ret;
void initTree() {
num = 2, suff = 2;
tree[1].len = -1;
tree[1].sufflink = 1;
tree[2].len = 0;
tree[2].sufflink = 1;
}
bool addLetter(int u) {
int cur = suff, curlen = 0;
int let = s[u] - 'a';
while (true) {
curlen = tree[cur].len;
if (u - 1 - curlen >= 0 && s[u - 1 - curlen] == s[u]) break;
cur = tree[cur].sufflink;
}
if (tree[cur].next[let]) {
suff = tree[cur].next[let];
return false;
}
suff = ++ num;
tree[num].len = tree[cur].len + 2;
tree[cur].next[let] = num;
if (tree[num].len == 1) {
tree[num].sufflink = 2;
tree[num].num = 1;
return true;
}
while (true) {
cur = tree[cur].sufflink;
curlen = tree[cur].len;
if (u - 1 - curlen >= 0 && s[u - 1 - curlen] == s[u]) {
tree[num].sufflink = tree[cur].next[let];
break;
}
}
tree[num].num = 1 + tree[tree[num].sufflink].num;
return true;
}
int main() {
cin >> s;
initTree();
for (int i = 0; i < s.size(); i ++ ) {
addLetter(i);
ret += tree[suff].num;
}
cout << ret - s.size();
return 0;
}
T3
题目描述
给定一个字符串,请返回满足以下条件的最长字符串的长度:“a”、“b”、“c”、
“X”、“Y”、“Z”在字符串中都恰好出现了偶数次(0也是偶数)
输入描述
字符串s,$s长度 \geq 1$
输出描述
一个整数,满足条件的最长字符串的长度
示例1
样例输入
amabc
样例输出
3
说明
ama,长度为3
算法
(暴力枚举) $O(n ^ 2)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
string s;
vector<char> need = {'a', 'b', 'c', 'x', 'y', 'z'};
int ret;
bool check(string s, char c) {
int cnt = 0;
for (auto x: s) if (x == c) cnt ++ ;
return cnt % 2 == 0;
}
int main() {
cin >> s;
for (int len = s.size(); len >= 1; len -- ) {
bool has_found = false;
for (int l = 0; l + len - 1 < s.size(); l ++ ) {
int r = l + len - 1;
bool is_valid = true;
for (auto c: need)
if (!check(s.substr(l, len), c)) {
is_valid = false;
break;
}
if (is_valid) ret = max(ret, len), has_found = true;
}
if (has_found) break;
}
cout << ret;
return 0;
}
T4
题目描述
网易公司在七夕节前后内部都会组织相亲活动,但由于人数众多,为了提高效率,主办方设计了一个系统。所有男生先登录系统,观看女生资料,然后在系统中登记他们自己有初步意向的女生,可以登记多个。反之女生也可以在系统中登记多个有初步意向 的男生。如果某个女生和某个男生同时互相都有意向,则认定为匹配。最终系统会取出所有系统互相都初步匹配的那类人男生女生,尽量地促成他们的真实约会,约会形式是互相匹配的一男和一女单独约会,但是被选中的男生女生最多只能约会一次。问该系统最多能够促成多少次约会,让尽可能多的男生女生得到约会机会。
输入描述
第一行输入为所有男生的id序列,$0 < id数量 < 10000$,用空格切分
第二行输入为所有女生的id序列,$0 < id数量 < 10000$,用空格切分
第三行为有已经有多少匹配数$n$
下面有$n$行,每一行为已经初步互相匹配的男生女生id对,为两个数字,第一个为男生id,第二个为女生id,用空格区分
输出描述
一个整数,最多能够促成多少次约会
示例1
样例输入
0 1 2
3 4 5
6
0 4
0 3
1 3
1 4
2 5
2 4
样例输出
3
说明
该case存在有多个互相匹配的情况,但经过分析,0-3,1-4,2-5这种约会安排方法,保证尽量多的约会,同时每人只约会最多一次。
算法
(二分图的最大匹配) $O(nm)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = N * N / 2;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
string s;
int n;
vector<int> boy, girl;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool find(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!st[j]) {
st[j] = true;
if (!match[j] || find(match[j])) {
match[j] = u;
return true;
}
}
}
return false;
}
int main() {
int x;
getline(cin, s);
stringstream l(s);
while (l >> x) boy.push_back(x);
getline(cin, s);
stringstream r(s);
while (r >> x) girl.push_back(x);
cin >> n;
memset(h, -1, sizeof h);
for (int i = 0; i < n; i ++ ) {
int a, b; cin >> a >> b;
add(a, b);
}
int ret = 0;
for (int i = 0; i < boy.size(); i ++ ) {
memset(st, false, sizeof st);
if (find(boy[i])) ret ++ ;
}
cout << ret;
return 0;
}

